II. APIBRĖZTINIS INTEGRALAS

Individualios uzduotys:

trumpa teorijos apzvalga,

pavyzdziai,

uzduotys savarankiskam darbui.

Apibrėztinių integralų skaičiavimas............................2 psl.

Netiesioginiai integralai.......... ..... ...... ................12 psl.

Apibrėztinių integralų taikymas geometrijoje..........20 psl.

Isspręstosios uzduotys

Apibrėztinių integralų skaičiavimas ..........................27 psl.

Netiesioginiai integralai.......... ..... ...... .................35 psl.

Apibrėztinių integralų taikymas geometrijoje...........38 psl.

Individualios uzduotys

Apibrėztinių integralų skaičiavimas

Jei funkcijos f(x) pirmykstė yra F(x), tai apibrėztiniam integralui teisinga Niutono ir Leibnico formulė:

.

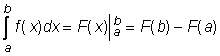Apibrėztiniame integrale 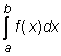pakeitus integravimo kintamąjį pagal lygybę arba t=u(x), reikia apskaičiuoti ir naujus integravimo rėzius: t₁ = u(a), t₂ = u(b).

Tuomet

= .

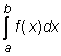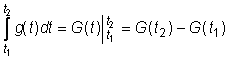Integravimo dalimis formulė apibrėztiniam integralui yra tokia:

.

Apibrėztinis integralas 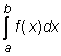pasizymi adityvumo savybe:

= +

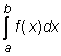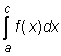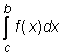
Pavyzdziai

1)

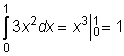
2) = - = = .

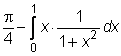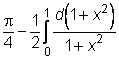Keičiame integravimo kintamąjį pagal lygybę: t = 1 + x². Kin­ta­mojo t rėziai: t₁ = 1, t₂ = 2.

Tuomet gauname:

= = .

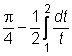2 uzdavinys. Apskaičiuokite apibrėztinius integralus

1) , , ,

,

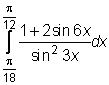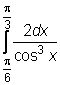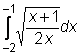2) , , ,

,

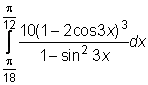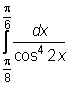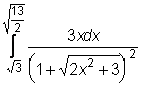3) , , ,

,

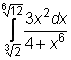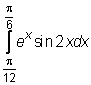4) , , ,

,

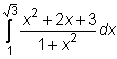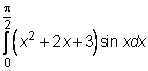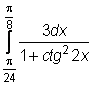
5) , , ,

,

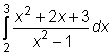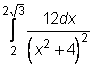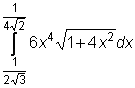6) , , ,

,

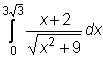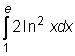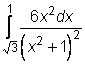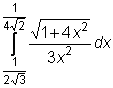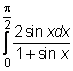
7) , , ,

,

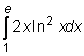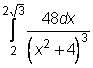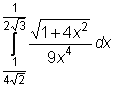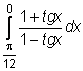
8) , , ,

,

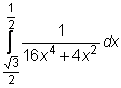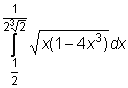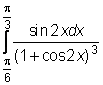
9), ,

, ,

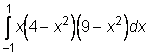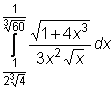10) , , ,

,

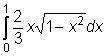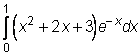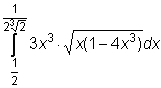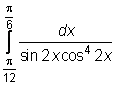
11) , , ,

,

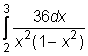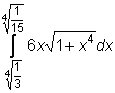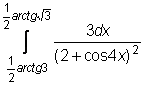
12) , , ,

,

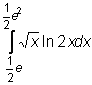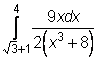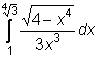13) , , ,

,

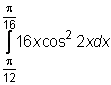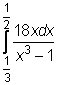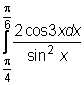
14) , ,

, ,

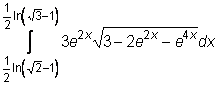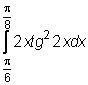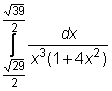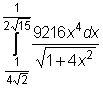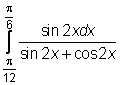
15) , , ,

,

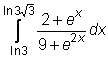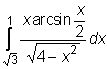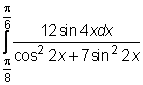
16) , , ,

,

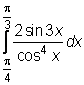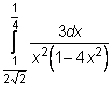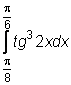
17) , ,

, ,

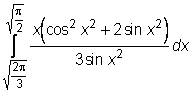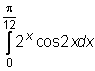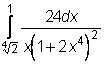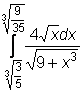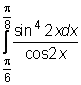
18) , , ,

,

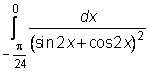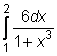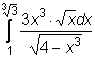19) , , ,

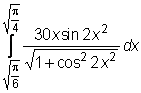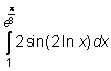21) , , ,

,

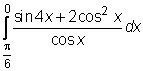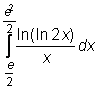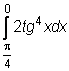
22) , , ,

,

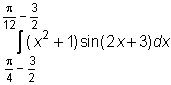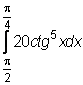
23) ,

, ,

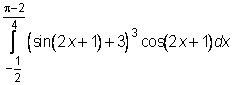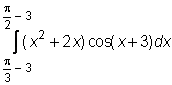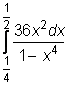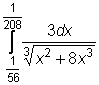
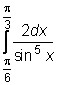
24) , ,

, ,

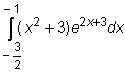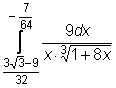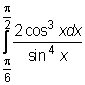
25) ,,

, ,

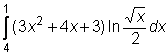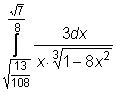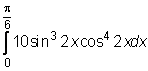
26) , ,

, ,

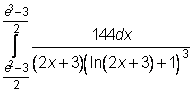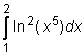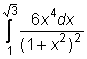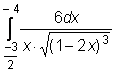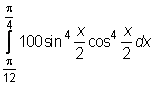
27) , , ,

,

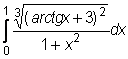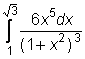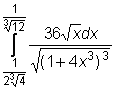28) , ,

, ,

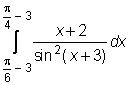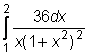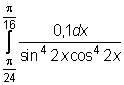
29) , , ,

,

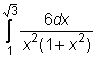30) , ,

, ,

Netiesioginiai integralai

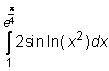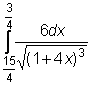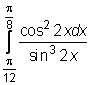
Netiesioginiais vadinami integralai su begaliniais rėziais arba neaprėztosios funkcijos integralai. Jų apibrėzimai:

, ,

;

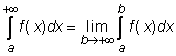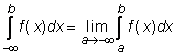jei a yra pointegralinės funkcijos f(x) begalinio trūkio taskas , tai

;

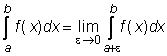jei b yra f(x) begalinio trūkio taskas, tai

;

jei c yra funkcijos f(x) begalinio trūkio taskas (a < c < b), tai

+ .

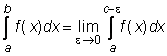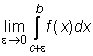Kai uzrasytosios ribos yra skaičiai, netiesioginiai integralai va­di­nami konverguojančiaisiais, o kai ribos yra begalinės arba neegzistuoja, netiesioginiai integralai vadinami diver­guo­jan­čiai­siais.

Netiesioginis integralas geometriskai reiskia begalinės srities plotą.

Pavyzdziai

1) Apskaičiuosime netiesioginį integralą .

Pagal apibrėzimą: = =

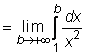= 1.

2) Apskaičiuosime netiesioginį integralą .

Kadangi pointegralinė funkcija yra lyginė, tai:

= = =

= = .

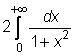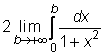3) Apskaičiuosime netiesioginį integralą .

Pointegralinė funkcija taske x = 0 yra neaprėztoji. Todėl:

= = = .

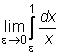Taigi sis integralas diverguoja.

4 uzdavinys. Apskaičiuokite netiesioginius integralus:

1)

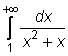
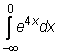
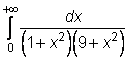
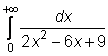
2)

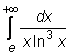
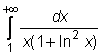
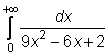
3)

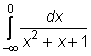
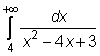
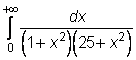
4)

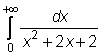
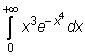
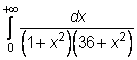
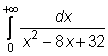
5)

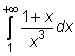
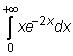
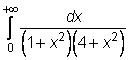
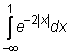
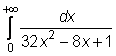
6)

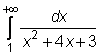
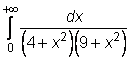
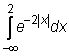
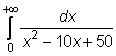
7)

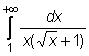
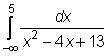
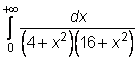
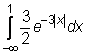
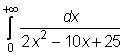
8)

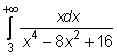
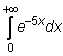
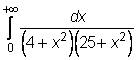
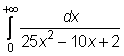
9)

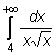
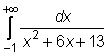
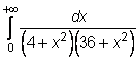
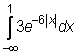
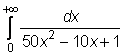
10)

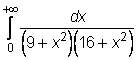
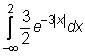
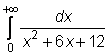
11)

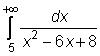
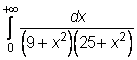
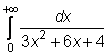
12)

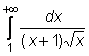
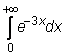
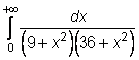
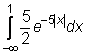
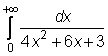
13)

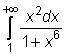
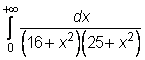
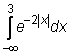
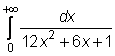
14)

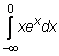
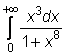
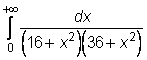
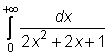
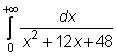
15)

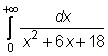
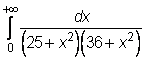
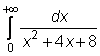
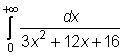
16)

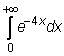
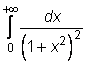
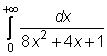
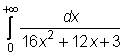
17)

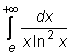
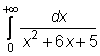
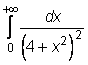
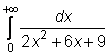
18)

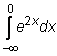
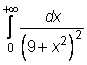
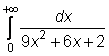
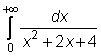
19)

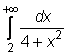
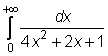
20)

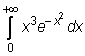
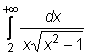
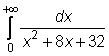
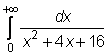
21)

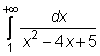
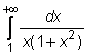
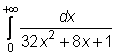
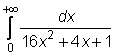
22)

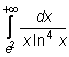
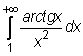
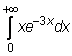
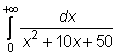
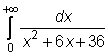
23)

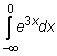
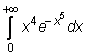
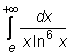
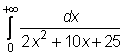
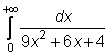
24)

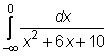
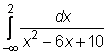
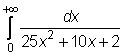
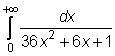
25)

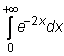
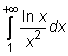
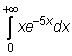
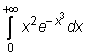
26)

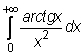
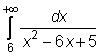
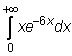
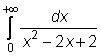
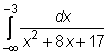
27)

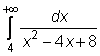
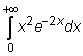
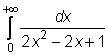
28)

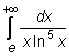
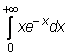
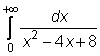
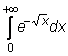
29)

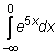
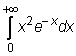
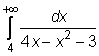
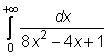
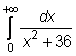
30)

Apibrėztinių integralų taikymas geometrijoje

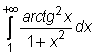
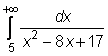
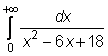
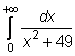
7 uzdavinys. Kreivinę trapeciją riboja kreivė, Ox asies atkarpa ir nė vienos, viena arba dvi vertikaliosios tiesės. Pavaizduokite sukinį apie Ox asį ir 0,001 tikslumu apskaičiuokite jo tūrį V_x.

8 uzdavinys. Kreivės lankas sukamas apie Ox asį. Pavaizduokite sukimosi pavirsių ir 0,001 tikslumu apskaičiuokite jo plotą S_x.

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13) 14)

15)

16)

17)

18)

19)

20)

21)

22)

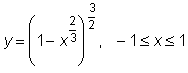
23)

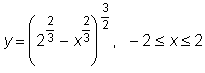
24)

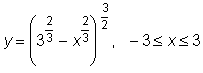
25)

26)

27)

28)

29)

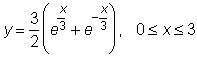
30)

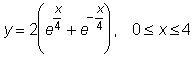
2. Isspręstosios uzduotys

Apskaičiuokite apibrėztinius integralus

Keičiame integravimo kintamąjį pagal lygybę t sinx.

Tada kintamojo t rėziai:

Tuomet

Tuomet

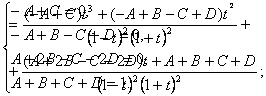
Is tapatybės (-A+C)t³+(-A+B-C+D)t²+(A+2B-C-2D)t+A+B+C+D rasime neapibrėztus koeficientus A, B, C ir D, sulyginę koeficientus prie vienodų t laipsniu:

Is sios sistemos gauname

Tuomet

Tuomet

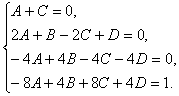
Is tapatybės (A+C)x³+(2A+B-2C+D)x²+(-4A+4B-4C-4D)-8A+4B+8C+4D rasime neapibrėztus koeficientus A, B, C ir D, sulyginę koeficientus prie vienodų x laipsniu:

Is sios sistemos gauname

Tuomet

Įvesime naują kintamąjį

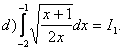
Tuomet

Ir tuomet

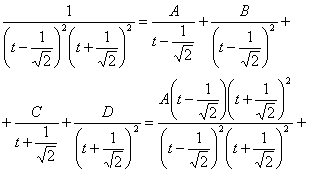
Tuomet

Is tapatybės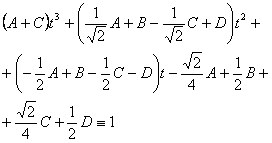

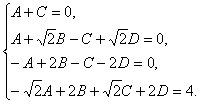
rasime neapibrėztus koeficientus A, B, C ir D, sulyginę koeficientus prie vienodų t laipsniu:

Is sios sistemos gauname

Tuomet

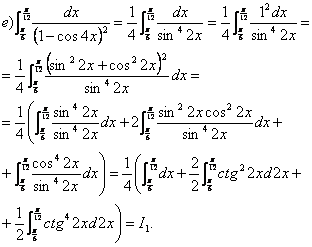
Įvedame naują kintamąjį

Tuomet

Netiesioginiai integralai

Apskaičiuoti netiesioginius integralus:

=

==

===

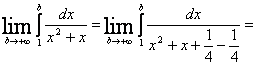
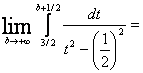
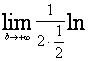
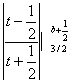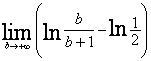= 1 -= -= .

(Integralas konverguoja).

=

===

== + .

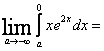
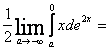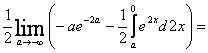
(Integralas diverguoja).

(Integralas konverguoja).

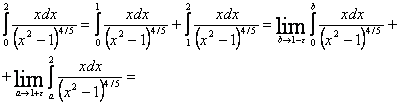
(Integralas konverguoja).

Apibrėztinio integralo taikymas geometrijoje

Apskaičiuoti plotą srities, ribojamos kreivių:

.

Tiesės ir parabolės susikirtimo taskus rasime is lygties

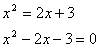
Pagal Vietos teoremą: .

Tuomet

.

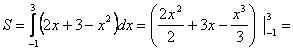
, tuomet .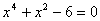

- neegzistuoja.

.

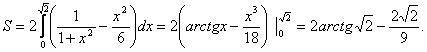
Is sąlygų isplaukia, kad .

Turime , arba , is kur isplaukia, kad

.

Tuomet .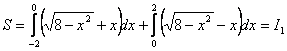

Įveskime naują kintamąjį Tuomet

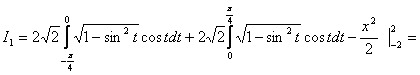
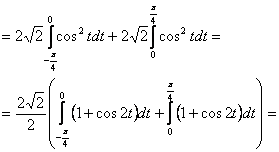
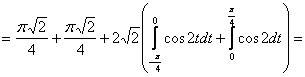
Apskaičiuokite kreivės lanko ilgį:

.

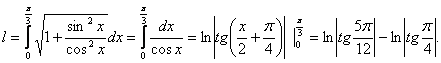
0. Is sąlygų isplaukia, kad

_.

.

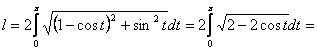
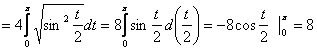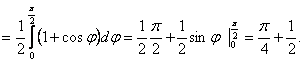
Apskaičiuokite tūrį sukinio, gaunamo sukant kreivę y=f(x) apie asį Ox:

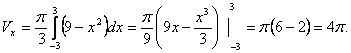
Apskaičiuokite sukimosi pavirsių, gaunamą sukant kreivę y=f(x) apie Ox asį:
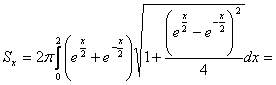
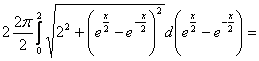