Isspręsti tiesinių lygčių sistemą Kramerio ir atvirkstines matricos metodais

1. Duota:

A = B =

Rasti: .

=

Ats:

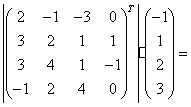
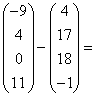
2. Isspręsti tiesinių lygčių sistemą Kramerio ir atvirkstines matricos metodais:

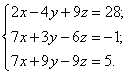
Spręsim Kramerio metodu:

Apskaičiuojam sistemos determinantą:

Kadangi , sistema turi tik vieną sprendinį. Norint jį apskaičiuoti, 13313w2220n reikia rasti dar 3 determinantus kurie gaunami is determinanto , pakeitus i-ajį stulpelį sistemos laisvųjų narių stulpeliu:

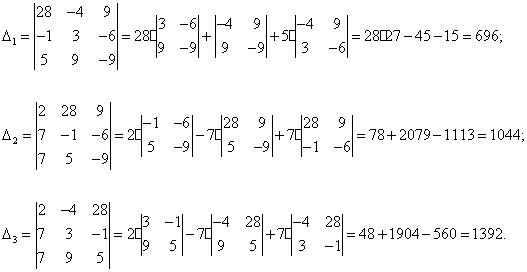
Naudojant Kramerio formules, gausim:

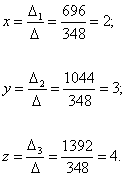
Spręsim sią lygčių sistemą atvirkstinės matricos metodu:

Turime rasti matricos

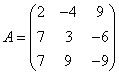atvirkstinę matricą

Sios matricos determinantą buvom apskaičiavę 1-oje sio uzdavinio dalyje:

48

Kadangi tai matrica A turi atvirkstinę matricą . Norėdami rasti jos elementus, apskaičiuosime determinanto elementų adjunktus:

Taigi, atvirkstinė matrica bus:

Tada nezinomųjų stulpelis bus:

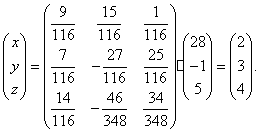
Kadangi abiem atvejais gavome tuos pačius atsakymus, galime manyti,kad jie teisingi.

Patikrinsim, įstatydami gautas saknis į pradinę sistemą:

.

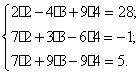Ats: (2; 3; 4).

3. Istirti tiesinių lygčių sistemos suderinamumą ir isspręsti sistemą Gauso metodu:

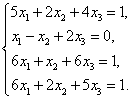
Jei,spręsdami Gauso metodu, sistemą pertvarkysim į trapecinę, ji bus suderinta.

Uzrasome sistemos isplėstąją matricą:

.

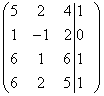Sukeičiame vietomis pirmąją ir antrąją eilutes:

.

Nekeisdami pirmosios eilutės, prie antrosios, trečiosios ir ketvirtosios eilučių pridedame pirmąją, padaugintą atitinkamai is -5, -6, ir -6:

.

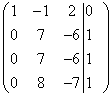Sukeitę vietomis antrąją ir ketvirtąją eilutes ir atėmę trečiąją eilutę is antrosios,gauname:

.

Prie ketvirtosios eilutės pridėsim trečiąją, padaugintą is -7:

.

Taigi, turime:

Atsakymas: .

4. Isspręsti tiesinio optimizavimo uzdavinį grafiniu būdu:

Sąlyga:

A ir B tipo gaminių gamybai naudojama trijų rūsių zaliava. A tipo gaminio vienam vienetui pagaminti reikia 12kg I rūsies zaliavos, 10kg II rūsies zaliavos ir 3kg III rūsies zaliavos. B tipo gaminio vienam vienetui pagaminti reikia 3kg I rūsies zaliavos, 5kg II rūsies zaliavos ir 6kg III rūsies zaliavos. Atitinkamų zaliavų atsargos yra 684kg, 690kg ir 558kg. Pelnas, realizavus vieną A tipo gaminį yra 6Lt, o vieną B tipo gaminį- 2Lt.

Sudaryti sių tipų gaminių gamybos planą, kad juos realizavus gautume didziausią pelną.

Sprendimas:

Sudarysim sio uzdavinio matematinį modelį. Pazymėkime planuojamo gaminti gaminio kiekį (j=1,2). Tada vektorius ir bus įmonės gamybos planas.

Bendras įmonės planas yra:

Bendras zaliavos kiekis, sunaudojamas gamybos planui įvykdyti yra:

Sis kiekis negali virsyti turimo zaliavos kiekio , todėl

Plano koordinatės turi būti neneigiamos, t.y.

Taigi, turim isspręsti tiesinio programavimo uzdavinį:

Arba

Plokstumoje pavaizduojame leistinųjų vektorių aibę X, vektorių c = (3;1) ir tiesę

Lygiagrečiai ,,stumdami" tiesę vektoriaus c kryptimi, randame labiausiai nutolusį aibės X taską A. Issprendę tame taske susikertančių tiesių lygčių sistemą

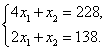
surandame tasko A koordinates Apskaičiuojame 366. taigi, sio uzdavinio optimalus sprendinys yra o

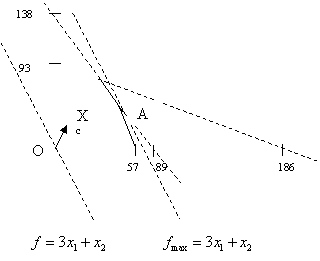
Pavaizduosim visa tai grafiskai:

Ats Norėdama gauti didziausią pelną, siekiantį 366 Lt, įmonė turi pagaminti 45 A tipo gaminius ir 48 B tipo gaminius.