Sa se calculeze
a) 0 ; b
; c) 3 ;d) 2 ;e) 1 f)
-
2.Sa se determine m real astfel incat sistemul liniar omogen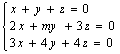 
, sa aiba si solutii
nenule.
a)m=0 b) m
c) m=3 d) m= -3 e) m=1 f) m=5
3.Sa se calculeze I=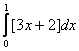
, unde [u] reprezinta partea i 23523m127x ntreaga a lui u.
a) I=0 b) I=2 c) I=4 d) I=6 e) I=5 f) I=3
4. Multimea solutiilor
ecuatiei 
este
:
a) 
b) d) e) f) ;
5.Sa se determine valorile parametrului real m,astfel incat ecuatia 
sa aiba trei solutii
reale distincte strict pozitive .
a) m
b) m=2 c) m
d) m=
e) 
f)
6. Multimea solutiilor
ecuatiei 
este
:
a) b) c) d) e) f)
7.Sa se determine numerele reale a,b astfel incat polinomul P=
sa fie divizibil cu 
a) a=9, b= - 6 b) a=b=3 c) a=0, b=1 d) a=9, b= -12 e) a= -9, b=12 f) a=12, b= -9
8.Multimea valorilor naturale ale lui n astfel incat 
este :
a) b) c) d) e) f) vida
9.Pe multimea R a numerelor reale se considera legea de compozitie interna 
10. Sa se calculeze
:
a) 2 b) 
c) 1 d) e) 0 f) -1
11. Sa se calculeze 
a) I=arctg 2; b) I=1; c) I=ln 2; d) I=arctg e; e) I= arctg 
f) I=
12. Solutiile sistemului :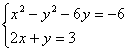 
sunt :
a) (1,1); b) (2,0)si(1`,1); c)1,7) si (1,11); d) (1,7); e) (1,-11); f) (7,-11) si (1,1).
13. Sa se calculeze numarul complex 
a) z=1; b) z=I; c) z=-1; d) z= 1+I; e) z=0; f) z=3.
Multimea solutiilor ecuatiei 
este;
a) vida; b) 
c) ; d) ; e) ; f) .
15. Fie matricea 
Sa se calculeze 
a) 
b) 
c) 
d) 
e) 
f) 
Sa se calculeze 
pentru functia 
a) 1; b)2; c)0; d) 3; e) -1; f) 7.
Sa se rezolve in R inecuatia 
a) 
b) 
c) 
d) 
e) 
f) 
Sa se determine valorile parametrului real m pentru care ecuatia 
are radacini reale si
distincte.
a) 
b) 
c) 
d) 
e)
f) 
|
