DIFRACŢIA LUMINII

DIFRACŢIA LUMINII

10.1. Introducere

Fenomenele de difractie desemneaza, în general, fenomene ondulatorii care se produc la propagarea luminii în medii cu neomogenitati suficient de mici astfel încât legile opticii geometrice nu mai sunt respectate.

Grimaldi (1665) observa prezenta luminii în umbra geometrica obtinuta pe ecranele opace (fig.10.1) si interpreteaza fenomenul ca o dislocatie a fasciculului luminos.

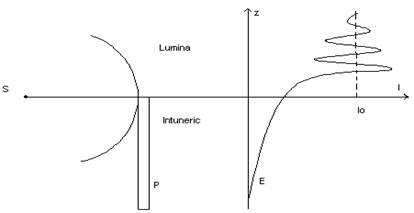
S - sursa punctiforma; (Σ) suprafata de unda; P-paravan opac;

E- ecran; În partea dreapta a figurii se reprezinta dependenta

I(z) vizibila pe ecran.

Fig. 10.1.

Difractia poate fi definita si ca fenomenul de "ocolire" de catre lumina a obstacolelor atunci când dimensiunile acestora sunt comparabile cu lungimea de unda a radiatiilor incidente si implica modificarea repartitiei spatiale a intensitatii unei unde datorita obstacolelor (aperturi si/sau paravane opace), modificare ce reprezinta franjele de difractie, fig.10.2.

Fig. 10.2. Umbra unei lame de ras

Datorita difractiei nu exista o frontiera neta între regiunea de umbra si regiunile luminoase atunci când lumina este incidenta pe obstacole de dimensiuni mici, iar în spatele obstacolului apar franje de difractie (distributia intensitatii luminii între valori maxime si minime).

În fenomenele de difractie spatiul fizic este de regula împartit în doua regiuni: regiunea surselor de lumina (I) si regiunea de difractie (II), printr-o suprafata de separatie (S) ce contine paravanele opace si aperturile, fig.10.3.

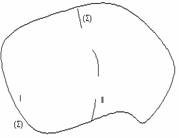
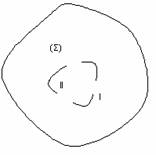
Fig. 10.3. Geometrii de difractie

Problema fundamentala a difractiei consta în determinarea câmpului electromagnetic în orice punct din spatiu, atunci când sunt cunoscute pozitiile si formele surselor luminoase, paravanelor opace si aperturilor ce produc difractia. Riguros, aceasta înseamna rezolvarea ecuatiilor Maxwell pentru marimile de stare ale câmpului, cu conditii la limita corespunzatoare, dependente de natura si proprietatile optice ale ecranelor. Un astfel de deziderat reprezinta teoria vectoriala a difractiei si experienta arata ca este destul de greu de relizat. Exista un numar limitat de cazuri particulare în care problema poate fi rezolvata analitic cu considerarea caracterului vectorial si al starilor de polarizare. În unele conditii însa, se pot introduce o serie de ipoteze simplificatoare care conduc la situatii aproximative în buna concordanta cu datele experimentale. Astfel teoria scalara sau optica a difractiei elaborata sub doua 17317w228r forme: teoria Huygens-Fresnel si teoria Kirchhoff-Sommerfeld are la baza o serie de ipoteze care transforma problema vectoriala într-una scalara.

10.2. Ipoteze ale studiului difractiei luminii în aproximatia optica

Dupa cum rezulta din experiente, fenomenele de difractie nu manifesta nici un efect sensibil de polarizare si, de asemenea, sunt independente de proprietatile materialelor ecranelor care le produc. Aceste doua constatari experimentale, împreuna cu observatia ca frecventele implicate sunt înalte, permit introducerea urmatoarelor ipoteze simplificatoare:

1° Unda electromagnetica vectoriala se înlocuieste cu o singura marime ondulatorie scalara complexa ce defineste perturbatia luminoasa functie de spatiu si timp, , si care se numeste amplitudine complexa. Amplitudinea complexa poate fi, de exemplu, una oricare dintre componentele rectangulare ale vectorilor sau.

2° Informatia necesara pentru a preciza "starea luminii" într-un punct la un moment dat este continuta în expresia, aceasta marime specificând amplitudinea, faza si intensitatea luminii. În particular, intensitatea luminii este proportionala cu modulul patrat al amplitudinii complexe:

(10.1)

În aceste ipoteze, obtinerea unei solutii riguroase a problemei difractiei necesita rezolvarea ecuatiei de propagare a undelor:

(10.2)

cu conditiile la limita corespunzatoare pe suprafata ecranelor (conditii care depind si de proprietatile optice ale materialelor). În ecuatia (10.2), este indicele de refractie al mediului în care se propaga lumina.

3° Toate cazurile sunt reduse cu ajutorul analizei Fourier, la cazul undelor monocromatice, adica se considera:

. (10.3)

Substituind (10.3) în ecuatia de propagare a undelor (10.2) se obtine o ecuatie de tip Helmholtz, independenta de timp:

(10.4)

unde este numarul de unda.

4° Urmeaza a se rezolva ecuatia Helmholtz (10.4) si se considera ca pe suprafata ecranelor pe care lumina se difracta:

(10.5)

5° Toate sursele emit lumina într-un mediu izotrop si atunci amplitudinea complexa are numai o variatie radiala:

astfel ca ecuatia (10.4) se scrie:

(10.6)

10.3. Teoria Huygens-Fresnel pentru difractia luminii în aproximatia optica

10.3.1. Principiul Huygens-Fresnel

În elaborarea teoriei ondulatorii a luminii, Huygens (1690) a introdus un principiu cu ajutorul caruia explica propagarea luminii în spatiu. Acest principiu de constructie pentru frontul de unda precizeaza ca: efectul unei surse primare S într-un punct oarecare P, exterior unei suprafete (S) poate fi înlocuit prin efectul produs de o repartitie continua de surse convenabil alese, situate pe suprafata (S), fiecare element al suprafetei atinse de unda comportându-se ca o sursa secundara de unde sferice a caror aplitudine este proportionala cu aria elementului de suprafata considerat, fig.10.4. Conform principiului lui Huygens fiecare punct al frontului de unda S(t) este considerat o sursa secundara de vibratii. Înfasuratoarea fronturilor de unda produse de sursele secundare da frontul de unda produs de sursa primara la un moment ulterior lui t, S(t+Δt), fig.10.5.

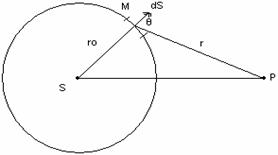
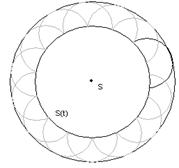
Fig. 10.4. Propagarea luminii în spatiu  Fig. 10.5. Principiul lui Huygens

Fresnel a completat principiul lui Huygens, în scopul rezolvarii problemei difractiei, cu postulatul interferentei mutuale a undelor secundare, deci, cu coerenta acestor unde, precizând ce trebuie înteles în principiul lui Huygens prin "surse convenabil alese": faza undelor secundare pe suprafata (S) este egala cu faza undei primare în fiecare punct sau element de pe (S), iar amplitudinea undei secundare este proportionala cu amplitudinea undei primare în zona sursei secundare. Ca urmare, sunt posibile corelatii cauzale între amplitudinile si fazele undelor secundare si cele cu care unda primara ajunge pe suprafata (S) (într-un mediu omogen si izotrop, frontul de unda coincide cu suprafata de unda), iar principiul Huygens-Fresnel reprezinta tocmai modalitatea de evidentiere cantitativa a acestor corelatii.

Fie suprafata sferica (S) o pozitie instantanee a frontului de unda generat de sursa punctiforma S si fie P punctul în care se doreste a fi determinata perturbatia luminoasa, fig.10.4. În acord cu principiul Huygens-Fresnel fiecare element de arie de pe suprafata (S) poate fi privit ca o sursa secundara de unde sferice; toate undele secundare fiind sincrone si de egala amplitudine. Contributia unui element de arie dS de pe suprafata (S) la perturbatia luminoasa din punctul P are expresia:

(10.7)

unde r₀ este raza frontului de unda, s-a omis factorul armonic e^-iωt, iar perturbatia în punctul M centrat pe elementul dS s-a considerat de forma , adica sursa S emite unde sferice de amplitudine A.

În relatia (10.7) coeficientul Kse numeste factor de oblicitate sau de înclinare si descrie variatia cu directia a amplitudinii undelor secundare. q este unghiul de difractie. Dupa Fresnel, coeficientul de oblicitate are valoarea maxima K=1 pentru θ=0, adica atunci când punctul M se afla pe axul optic principal SP si descreste rapid cu cresterea unghiului de difractie, devenind nul pentru , ceea ce înseamna, de fapt, anularea undelor regresive.

Intensitatea perturbatiei luminoase în punctul P este egala cu suma intensitatiilor perturbatiilor emise de sursele secundare, adica:

(10.8)

Integrala obtinuta se numeste integrala de difractie, iar evaluarea ei - daca este posibila - permite determinarea perturbatiilor luminoase în regiunea de difractie, în functie de factorul de oblicitate, de pozitia si forma aperturilor.

10.3.2. Metoda zonelor lui Fresnel

Aceasta metoda geometrica de rezolvare a problemelor de difractie permite calculul integralei (10.8) atunci când sistemul fizic este caracterizat de simetrie axiala.

Se considera o apertura curculara simetrica fata de axul optic principal pe care se afla sursa punctiforma S si punctul de observare P, fig.10.6. Frontul de unda sferic (S) este divizat în regiunea de difractie în mai multe parti concentrice numite zone Fresnel care sunt sursele elementare secundare. Zonele Fresnel se construiesc prin delimitarea unor regiuni pe frontul/suprafata de unda (S) considerând sferele cu centrul în P si de raze unde b este distanta VP, iar , n fiind numarul zonelor posibil de delimitat.

Zonele Fresnel sunt delimitate prin intersectia calotei sferice a frontului de unda cu centrul în S si de raza r₀ cu sferele ce au centrul în P si razele .

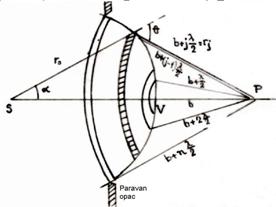
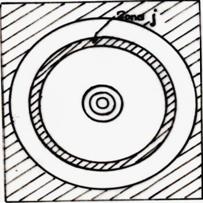
a)                                                b)

Fig. 10.6. Zonele Fresnel

Se considera ca în interiorul unei zone factorul de oblicitate este constant (K_j(θ)=K_j=const,) si, de asemenea, într-o zona Fresnel, faza undei este constanta. Undele secundare provenind de la doua zone Fresnel consecutive ajung în punctul P defazate cu , astfel încât interfera distructiv; perturbatia luminoasa rezultanta în punctul P fiind efectul unei interferente multiple a undelor care vin din toate zonele Fresnel construite. Se pot demonstra si urmatoarele doua proprietati ale zonelor Fresnel care se mai numesc si zone semiperioada: (1) ariile zonelor Fresnel sunt egale si (2) razele zonelor Fresnel variaza direct proportional cu radacina patrata a numerelor întregi.

Din fig. 10.6.a. se observa ca:

si prin diferentiere se obtine:

(10.9)

astfel ca aria elementara a unei zone Fresnel:

,

devine:

(10.10)

fiind unghiul azimutal.

Contributia zonei "j" la perturbatia luminoasa din punctul P este:

,

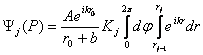adica:

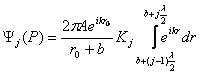. (10.11)

Dupa calcule se obtine:

(10.12)

efectul rezultant în P fiind:

. (10.13)

Suma:

(10.14)

se poate calcula prin metoda propusa de Schuster care considera ca coeficientul de înclinare are o descrestere monotona cu cresterea unghiului de difractie, astfel încât se poate presupune urmatoarea relatie de legatura:

(10.15)

Scriind suma S sub forma:

ultimul termen fiind:

daca n este impar si:

daca n este par si având în vedere relatia de legatura (10.15), rezulta:

(10.16)

cu semnul "+" daca n este impar si cu semnul "-" daca n este par.

Înlocuind în (10.13) rezultatele sumei se obtine expresia perturbatiei luminoase rezultante în punctul P:

(10.17)

Se observa ca rezultatul obtinut se poate scrie sub forma:

(10.18)

care arata ca perturbatia rezultanta în P este egala cu media aritmetica a contributiilor primei si ultimei zone.

Daca atunci pentru ultima zona Fresnel care se poate vedea din P, K_n=0 si din (10.18) rezulta:

(10.19)

adica perturbatia totala în P este egala cu jumatate din perturbatia datorata primei zone. Ecuatia (10.19) este în acord cu efectul undelor sferice daca:

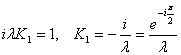. (10.20)

Termenul poate fi înteles presupunând ca undele secundare sunt defazate cu un sfert de perioada în raport cu undele primare, iar celalalt termen din relatia (10.20) se poate explica admitând ca în expresia undelor secundare se introduce un factor de amplitudine 1:λ.

Întrucât amplitudinile undelor provenite de la zone Fresnel diferite formeaza un sir descrescator, iar saltul de faza la trecerea de la o zona la urmatoarea este π radiani, amplitudinea rezultanta Ψ(P) poate fi obtinuta si grafic sub forma unei spirale cu raza descrescatoare, fig.10.7. Din ecuatia (10.13) se observa ca daca se obtureaza zonele Fresnel pare sau impare, se obtine o crestere semnificativa a intensitatii luminii în punctul P, concentratia radiatiei fiind asemanatoare cele produse de o lentila "cu mai multe focare". O astfel de apertura difractata în care s-a anulat efectul zonelor Fresnel pare sau impare se numeste retea zonala sau retea Soret.

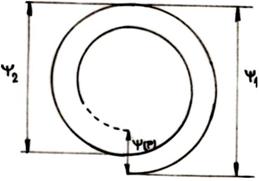
Fig.10.7.

În cazul în care punctul de observatie P nu se afla pe axa de simetrie a sistemului sau apertura nu este simetrica axului optic principal, atunci calculele se complica întrucât unele zone sunt partial obturate, iar în perturbatia rezultanta trebuie ponderate corespunzator contributiile diferitelor zone.

10.3.3. Clasificarea fenomenelor de difractie

În cazul în care sistemul fizic nu este caracterizat de simetrie axiala, metoda zonelor lui Fresnel nu este aplicabila si se cauta alte metode de rezolvare pentru integrala de difractie (10.8).

Daca paravanul opac (π) prevazut cu o deschidere (apertura) neregulata (Σ) se afla situat în planul z=0, atunci din fig. 10.8. se poate scrie:

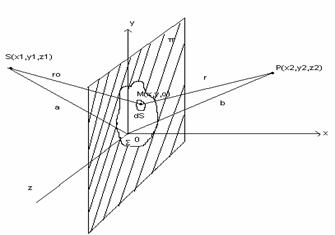
Fig. 10.8.

, (10.21)

unde:

(10.22)

Din relatia (10.21), folosind aproximatia:

valabila pentru valori mici ale lui α rezulta:

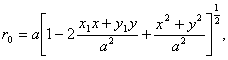
adica:

(10.23)

Un rationament analog conduce la urmatoarea expresie pentru r:

(10.24)

În fig.10.8 semispatiul z<0 reprezinta regiunea surselor; sursa punctiforma S având coordonatele (x₁,y₁,z_1­), iar semispatiul z>0 reprezinta regiunea de difractie; perturbatia luminoasa fiind calculata în punctul P de coordonate (x₂,y₂,z_2­). Elementul recurent de suprafata dS este centrat in punctul M de coordonate (x,y,0). Pentru dimensiuni ale aperturii nu prea mari, în integrala de difractie (10.8) se considera:

(10.25)

si având în vedere si relatiile (10.23),(10.24) se obtine:

(10.26)

unde:

(10.27)

sunt cosinusii directori ai directilor r₀ si respectiv r.

Problema dererminarii perturbatiei luminoase în punctul P s-a redus acum la evaluarea integralei (10.26) cu functia f(x,y) data de relatia (10.27).

În functie de posibilitatea de a neglija fie termenii liniari, fie termenii patratici în relatia (10.27) fenomenele de difractie se clasifica în difractie Fresnel sau difractie în lumina divergenta (fig.10.9.a) si respectiv difractie Fraunhofer sau difractie în lumina paralela (fig. 10.9.b,c). Clasificarea are în vedere faptul ca în cazul difractiei Fresnel, sursa S si punctul de observatie P sunt situate la distanta finita de apertura, pe când în cazul difractiei Fraunhofer, sursa S si punctul de observatie P se afla "la infinit" în raport cu pozitia aperturii.

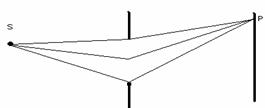
a) difractie Fresnel

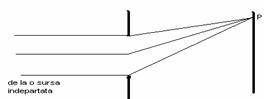
b) difractie Fraunhofer

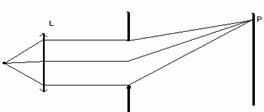
c) Conditii de difractie Fraunhofer produse cu lentile

Fig. 10.9.

10.3.4. Metoda integralelor lui Fresnel

Daca distantele dintre sursa si apertura si dintre apertura si punctul de observare sunt finite (comparabile cu dimensiunile geometrice ale aperturii) si în lipsa simetriei axiale a sistemului analizat, determinarea perturbatiei luminoase în punctul de observare se reduce la evaluarea integralei:

(10.28)

care se obtine din relatiile (10.26) si (10.27) prin neglijarea termenilor liniari în x si y.

Se face schimbarea de variabila:

, (10.29)

astfel ca integrala (10.28) devine:

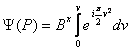. (10.30)

Evaluarea acestei integrale se face cu ajutorul functiilor:

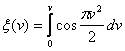(10.31)

si respectiv:

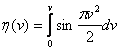(10.32)

numite integralele lui Fresnel. Integrala (10.30) se poate scrie acum:

(10.33)

si este imediat calculata întrucât valorile integralelor lui Fresnel sunt cunoscute, tab. 10.1. În fig.10.10. si 10.11. sunt reprezentate graficele celor doua integrale.

Tab. 10.1. Tabelul integralelor lui Fresnel

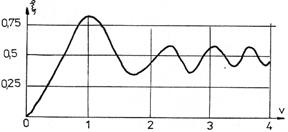
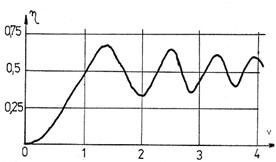
Fig. 10.10. Fig.10.11.

Pentru a determina perturbatia luminoasa în punctul P se poate utiliza constructia geometrica numita spirala lui Cornu. Aceasta este curba reprezentata parametric prin integralele lui Fresnel. Într-un sistem de axe tridimensional (ξ(v),v,η(v)) pentru diferite valori ale parametrului v se obtine o elice cu diametrul descrescator a carei proiectie în planul (ξ(v),η(v)) este spirala lui Cornu, fig.10.12.

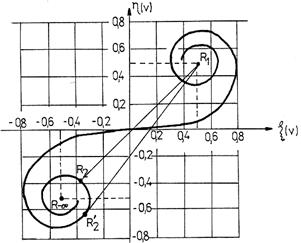
Fig. 10.12. Spirala lui Cornu

Se pot demonstra urmatoarele trei proprietati ale spiralei Cornu:

1° lungimea elementului de arc dl este determinata de variatia dv a parametrului v:

si atunci valoarea parametrului v într-un punct al curbei este egala cu lungimea curbei din origine pâna în acel punct;

2° înclinarea curbei într-un punct este proportionala cu patratul lungimii arcului în acel punct:

3° pentru v→∞ spirala lui Cornu tinde asimptotic catre punctul

10.3.5. Difractia Fraunhofer

În cazul difractiei Fraunhofer sau în lumina paralela distantele de la sursa la ecran si de la ecran la punctul de observare sunt foarte mari, fig.10.8 si în aceste conditii, termenii de ordin doi în variabilele x si y pot fi neglijati în expresia (10.27) a functiei f(x,y). Urmeaza ca trebuie evaluata integrala:

(10.34)

unde s-a notat cu p=l₁-l₂ si q=m₁-m₂, iar este numarul de unda. Evident, valoarea perturbatiei luminoase obtinuta în punctul de observare P depinde de forma aperturii.

a). Difractia Frounhofer pe o apertura dreptunghiulara

Se considera o apertura de forma dreptunghiulara cu laturile 2a si 2b ca în fig.10.13.

 

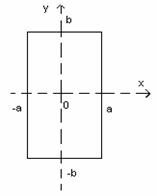
Fig. 10.13. Fig.10.14.

În aceste conditii se poate aplica metoda separarii variabilelor, iar integrala (10.34) devine:

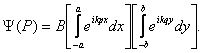(10.35)

adica:

sau:

(10.36)

unde S=4ab este aria suprafetei aperturii.

Întrucât intensitatea luminii în punctul P este proportionala cu patratul perturbatiei luminoase I≈|Ψ|² rezulta:

(10.37)

unde I₀=const. este intensitatea luminii în centrul aperturii. Imaginea obtinuta este ilustrata în fig.10.14.

În cazul unidimensional: a finit, b>>a, b→∞, integrala de variabila y din (10.35) da o valoare constanta proportionala cu lungimea b a fantei si atunci perturbatia luminoasa în punctul P se scrie:

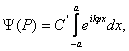(10.38)

unde C'=const.

Rezolvând integrala (10.38) se obtine:

sau:

(10.39)

unde C este o constanta proportionala cu aria suprafetei aperturii (C≈BS).

Intensitatea luminii este în acest caz unidimensional:

(10.40)

si are valorile minime I_min=0 pentru:

Valorile maxime ale intensitatii sunt date de conditia dI/d(kpa)=0, rezultând ecuatia transcendenta: tg(kpa)=kpa ale carei solutii:

Kpa=0; 1,43π; 2,46π; 3,47π; 4,47π;......

se obtin grafic sau numeric. Dependenta I(pka) este data în fig.10.15.

Din fig.10.16 se observa ca în cazul unidimensional al difractiei Frounhofer al unui fascicul de lumina incident sub unghi θ₀ si difractat sub un unghi θ de o apertura de deschidere a se poate scrie:

,

unde:

este diferenta de drum optic dintre cele doua raze de lumina.

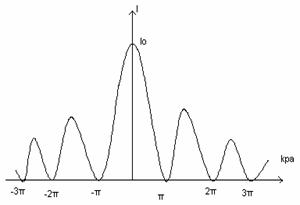
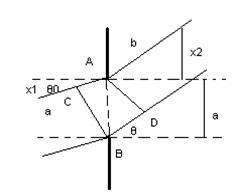
Fig. 10.15. Fig.10.16.

b). Difractia Frounhofer pe o apertura circulara

Se considera o apertura circulara de raza R si se lucreaza în coordonate polare (ρ,φ), ρ[o,R], φ[0,2π], fig.10.17. Daca coordonatele punctului recurent de pe apertura sunt:

iar coordonatele punctului P fata de imaginea geometrica a sursei sunt:

cu:

unde ω este sinusul unghiului facut de directia (p,q), cu directia axului optic principal (p=q=0), atunci integrala de difractie (10.34) devine:

(10.41)

Având în vedere reprezentarea integrala a functiilor Bassel J_n(z):

,

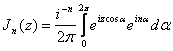relatia (10.41) se reduce la:

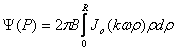
si apoi:

, (10.42)

daca se particularizeaza relatia de recurenta:

În rezultatul (10.42), J₁(kωρ) este functia Bessel de spata întâi si ordin unitar.

Intensitatea luminii este:

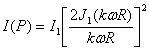(10.43)

si reprezinta o succesiune de inele luminoase si întunecate, fig.10.18, centrul luminos al figurii de difractie fiind numit discul lui Airy.

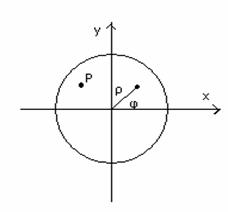
Fig. 10.17. Fig. 10.18.

Punctele de minim ale figurii de difractie se obtin pentru valorile minime ale functiei Bessel, fig.10.19.

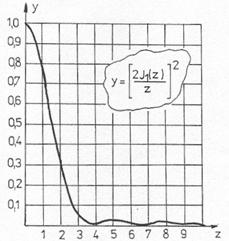
Fig. 10.19.

10.3.6. Difractia Frounhofer pe o retea de difractie plana în transmisie

Reteaua de difractie plana este constituita dintr-un sistem de N fante dreptunghiulare identice, paralele, echidistante si coplanare având dimensiuni transversale mult mai mici decât dimensiunile longitudinale. Practic, o retea de difractie optica este confectionata din sticla (sau un alt material transparent optic) pe care sunt trasate zgârieturi paralele echidistante, foarte dese (500÷1000 trasaturi pe mm). Zonele zgâriate reprezinta regiuni opace, iar cele ramase libere sunt regiunile transparente ce au rolul fantelor.

Daca a este largimea unei fante, iar b este largimea zonei opace, atunci:

(10.44)

reprezinta perioada retelei, unde n este constanta de retea, fig.10.20.

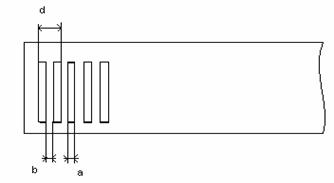
Fig. 10.20.

Se considera un fascicul de lumina paralel sub un unghi de incidenta θ₀ pe o retea de difractie plana cu un numar de N fante si o perioada de retea data de relatia (10.44) si se studiaza distributia intensitatii difractate în punctul de observare P (planul focal al lentilei convergente L), fig.10.21.

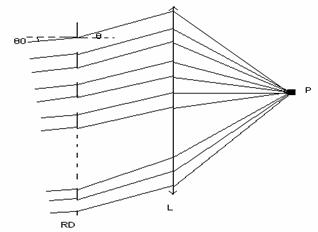
RD-retea de difractie (plana în transmisie)

L - lentila convergenta

Fig. 10.21.

La trecerea luminii prin reteaua de difractie are loc suprapunerea a doua fenomene: difractia luminii prin fiecare fanta si interferenta fasciculelor multiple care vin de la fante. Cu alte cuvinte, distributia intensitatii difractate se obtine printr-un fenomen de interferenta multipla a fasciculelor emise de cele N fante, fiecare fanta producând o figura de difractie proprie, iar determinarea perturbatiei luminoase în punctul de observare implica evaluarea expresiei:

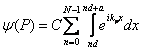
sau:

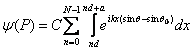, (10.45)

daca se are în vedere relatia (10.38) si geometria din fig.10.16.

Dar:

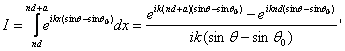
adica:

(10.46)

unde:

(10.47)

(10.48)

Înlocuind rezultatul (10.46) în expresia (10.45) a perturbatiei luminoase rezultante în punctul P se obtine:

sau:

(10.49)

daca se are în vedere suma progresiei geometrice de ratie :

constanta c complexa fiind egala cu C/i.

Intensitatea luminii în P este proportionala cu produsul dintre functia data de relatia (10.49) si complex conjugata sa:

.

Cum:

rezulta:

, (10.50)

care arata ca unda difractata de o retea plana poate fi considerata o unda de intensitate modulata de factorul , fig.10.22.

Conditia de obtinere a maximelor principale se scrie în cazul retelei de difractie sub forma:

de unde rezulta ecuatia retelei de difractie:

. (10.51)

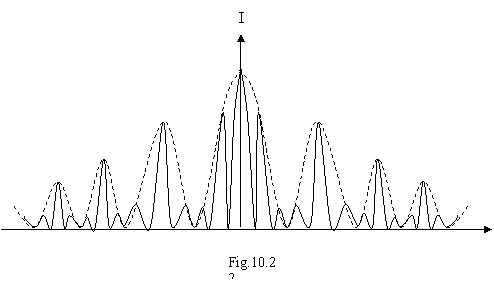
Se observa ca figura de difractie se caracterizeaza printr-o succesiune de maxime principale si secundare ca si în cazul interferentei multiple; factorul modulator are ca efect scaderea intensitatii maximelor principale pe masura departarii de maximul principal central.

Cu cât numarul de fante este mai mare, cu atât exista o detasare mai neta între pozitia maximelor principale si pozitia maximelor secundare, ceea ce face ca reteaua de difractie sa fie folosita ca un dispozitiv spectroscopic în determinarea cu precizie a lungimilor de unda. Primele retele de difractie au fost realizate de catre Fraunhofer (1821) si aveau 130 fante pe cm. Cu ajutorul lor au fost descoperite liniile Fraunhofer: liniile întunecate care apar în spectrul continuu al Soarelui. Ulterior, Rowland a perfectionat retelele de difractie ajungând la un numar de 8000 fante pe cm si a elaborat teoria retelelor de difractie concave. În prezent, prin metode interferometrice si holografice se construiesc retele cu un numar de peste 10⁵ fante pe cm.

10.3.7. Puterea de separare a instrumentelor optice

Obtinerea imaginilor stigmatice cu instrumentele optice implica respectarea criteriului lui Rayleigh care precizeaza conditiile care trebuie îndeplinite pentru ca doua puncte distincte sa dea printr-un sistem optic imagini distincte. Într-un sistem optic oarecare, imaginile a doua puncte luminoase nu vor fi punctiforme ci vor avea o structura datorita fenomenului de difractie: maxim central si maxime secundare alternând cu minime echidistante. Daca punctele luminoase sunt foarte apropiate, structurile produse prin difractie se suprapun si imaginile punctelor nu mai sunt distincte. Conform criteriului lui Rayleigh imaginile celor doua puncte mai pot fi vazute distinct daca maximul principal de difractie apartinând uneia din imagini se suprapune peste primul minim corespunzator celei de-a doua imagini de difractie.

Se defineste dispersia unghiulara , D, ca raportul dintre deviatia unghiulara dθ si diferenta dintre lungimile de unda care o produce:

. (10.52)

Daca dλ reprezinta cea mai mica diferenta dintre lungimile de unda pentru care se mai pot obtine imagini distincte, atunci marimea:

(10.53)

defineste puterea de rezolutie sau de separare cromatica a unui aparat spectral.

Între puterea de rezolutie si dispersia unghiulara se stabileste relatia de legatura:

. (10.54)

În cazul în care radiatiile incidente pe o retea de difractie plana sunt nemonocromatice pentru fiecare maxim de difractie se obtine un spectru al radiatiei incidente; reteaua de difractie fiind în acest caz un aparat dispersiv.

Presupunând o incidenta normala pe retea (­­­­­­­θ₀=0) ecuatia retelei (10.51) devine:

(10.55)

si prin diferentierea acestei relatii se obtine urmatoarea expresie a dispersiei unghiulare:

. (10.56)

Conform acestei relatii se constata ca în cazul retelei de difractie dispersia unghiulara este independenta de numarul N de fante al retelei si este cu atât mai mare cu cât constanta de retea este mai mare.

Pentru a stabili puterea de rezolutie a unei retele de difractie se aplica criteriul lui Rayleigh. Astfel din conditia de suprapunere a maximului principal de difractie cu primul minim adiacent corespunzând unghiului de deviatie θ+dθ:

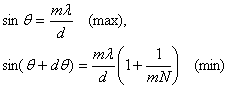
rezulta, în ipoteza unghiurilor θ mici expresia:

P=mN,

conform careia puterea de separare a unei retele creste cu numarul de linii si cu ordinul de difractie.

si în cazul unui punct luminos, imaginea acestuia data de o lentila sau un obiectiv nu este punctuala. Fenomenul de difractie care apare datorita aperturii circulare a lentilei face ca imaginea sa aiba o structura formata dintr-un maxim luminos central (discul Airy) înconjurat de inele concentrice alternativ întunecate si luminoase. Considerând conditii de difractie Fraunhofer, primul minim de difractie pe o apertura circulara de diametru D este dat de relatia:

Dsin θ=1,22λ.

Daca θ este unghiul de deviatie pentru care imaginile mai ramân distincte atunci:

(10.57)

ce reprezinta prin definitie inversul puterii de rezolutie a obiectivului.

10.4. Teoria Kirchhoff-Somerfeld pentru difractia luminii în aproximatia optica

Teoria propagarii undelor luminoase se poate dezvolta rezolvând ecuatia Helmholtz:

(10.58)

pentru perturbatia luminoasa ψ(r) cu ajutorul metodei lui Green.

Conditiile la limita considera ca pe suprafata ecranelor opace amplitudinea complexa si gradientul normal al acesteia (dupa directia normalei exterioare la suprafata) sunt nule, adica:

si (pe ecrane opace). (10.59)

În aperturi amplitudinea complexa si gradientul sau normal (dupa directia normalei exterioare la suprafata) au valori egale cu cele în cazul propagarii libere (în lipsa ecranelor si paravanelor):

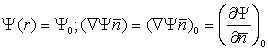. (10.60)

În aceste conditii, considerând geometria de difractie din fig.10.23, unde S este sursa de lumina, P este punctul de observatie, iar M este punctul care centreaza elementul de arie recurent de pe suprafata care separa regiunea de difractie (II) de regiunea surselor (I), se cauta o metoda de rezolvare a ecuatiei (10.58).

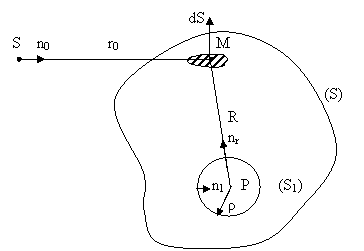
Fig.10.23.

Se considera marimea vectoriala:

(10.61)

unde φ,ψ sunt functii scalare continue cu variatie radiala în volumul V_S marginit de suprafata S care satisfac ecuatia undelor (10.58) si corespund aceleiasi valori k. Din teorema lui Gauss din analiza vectoriala:

rezulta:

(10.62)

ce reprezinta prima identitate a lui Green.

Prin permutarea se obtine relatia:

(10.63)

care scazuta din (10.62) conduce la expresia celei de-a doua identitate Green:

. (10.64)

Întrucât ambele functii sunt solutii ale ecuatiei undelor (10.58), membrul drept al egalitatii (10.64) se anuleaza, rezultând ecuatia:

, (10.65)

numita teorema lui Green.

10.4.1. Teoria lui Kirchhoff

Kirchhoff considera ca functia ψ este amplitudinea complexa ce caracterizeaza perturbatia luminoasa si care trebuie determinata în punctul P, ψ(P), iar functiei φ, care este vazuta ca o functie matematica auxiliara cu care se "sondeaza" regiunea de difractie, îi propune expresia:

. (10.66)

Se observa ca φ(r) reprezinta partea spatiala a unei unde sferice de amplitudine unitara având originea (sursa) în punctul P. Evident functia φ(r), (10.66), este solutie a ecuatiei Helmholtz a undelor (10.58) dupa cum se poate verifica imediat.

Calculul perturbatiei luminoase în punctul P, ψ(P), din teorema lui Green (10.65) utilizând functia φ(r) data de relatia (10.66) este împiedicat de expresia de acestei functii, întrucât tocmai în punctul P functia φ prezinta o singularitate infinita.

Pentru a elimina aceasta dificultate, se înconjoara punctul P cu o suprafata sferica S₁ cu centrul în P si de raza ρ. În aceste conditii, se va considera ca domeniul de integrare este dat de reuniunea suprafetelor (S) si (S₁):

,

adica:

, (10.67)

unde si sunt versorii elementelor de arie dS si respectiv dS₁, având directia si sensul normalelor exterioare la suprafata. În final, se va calcula limita când raza ρ a sferei S₁ tinde la zero pentru cea de-a doua integrala din ecuatia (10.67).

Înlocuind expresia functiei j(r) si trecând la limita rezulta:

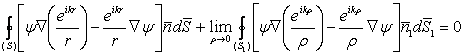. (10.68)

Se noteaza:

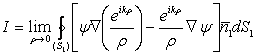
si se efectueaza operatiile de derivare vectoriala dupa directia versorului :

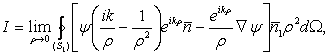(10.69)

unde: dΩ=dS₁/ρ² este unghiul solid sub care se vede elementul de arie dS₁ din punctul P.

Înmultind în paranteza dreapta cu ρ² si cum, la limita , se obtine:

(10.70)

astfel ca, dupa înlocuirea în ecuatia (10.68) rezulta:

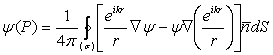. (10.71)

Relatia obtinuta se numeste formula lui Kirchhoff pentru difractia optica sau integrala Kirchhoff-Helmholtz si reprezinta o solutie a ecuatiei undelor (10.58), daca se cunoaste functia ψ si pretutindeni pe suprafata (S).

În ipotezele (10.59) si (10.60) formula lui Kirchhoff se reduce la expresia:

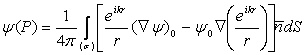, (10.72)

unde integrarea se face numai pe aperturile (σ) ale suprafetei (S).

Pentru rezolvarea ecuatiei (10.72) se are în vedere ca si conditie suplimentara ca pentru suprafetele mult departate de punctul de observare P, adica pentru suprafetele aflate "la infinit", functiile ψ si devin arbitrar de mici. Acest fapt se poate explica presupunând ca radiatia nu exista tot timpul, iar pentru punctele de pe o suprafata aflata "la infinit" câmpul radiatiei nu se poate propaga la acea distanta în timpul în care ia nastere perturbatia luminoasa în punctul P.

Utilizând relatia (10.72) se poate determina perturbatia luminoasa în punctul P pentru diferite cazuri particulare.

a). Unda incidenta sferica

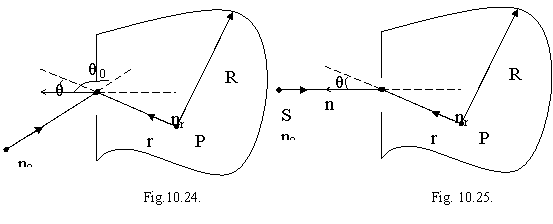
Particularizând fig.10.23 se considera ca sursa punctiforma S emite o unda sferica de amplitudine A, paravanul care contine apertura (σ) fiind plan, fig.10.24. Înlocuind expresia undei incidente:

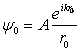(10.73)

în expresia (10.72) si efectuând operatiile de derivare vectoriala dupa versorii directiilor corespunzatoare rezulta:

. (10.74)

Deoarece, practic r₁r₀>>λ, unde λ este lungimea de unda a radiatiei incidente:

(unde k=2p

astfel încât termenii si se pot neglija în relatia (10.74) si rezulta:

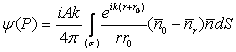
ce reprezinta integrala de difractie Fresnel-Kirchhoff si care se poate scrie sub forma:

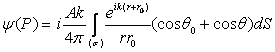, (10.76)

unde : si .

b). Unda incidenta plana

În acest caz se considera:

si presupunând ca fronturile de unda sunt paralele cu ecranul ce contine apertura (σ), fig.10.25, din (10.76) rezulta:

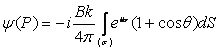, (10.77)

unde 1+cosθ reprezinta înclinatia Stokes. Din fig.10.25 se observa ca:

Problemele de difractie care se pot rezolva cu ajutorul teoriei lui Kirchhoff se reduc la un numar limitat si mic de cazuri care nu implica dificultati matematice prea mari. Astfel trebuie considerate ecrane plane, subtiri si opace prevazute cu aperturi libere sau formate din materiale transparente, de asemenea plane.

Din punct de vedere fizic, ipotezele (10.59) si (10.60) sunt inconsistente reprezentând o idealizare grosiera a fenomenului real în regiunile libere ale ecranului (pe aperturi) si în regiunile opace ale acestuia. Utilizarea aproximatiei Kirchhoff se justifica numai daca lungimile de unda ale radiatiei incidente sunt suficient de mici în raport cu dimensiunile aperturilor, iar punctele de observare ale câmpului electromagnetic difractat sunt mult departate de ecranul prevazut cu aperturi.

Din punct de vedere matematic, ipotezele (10.59) si (10.60) sunt inadmisibile chiar si într-o teorie aproximativa, deoarece o solutie oarecare a ecuatiei de propagare a undelor (10.58) se anuleaza în tot spatiul daca cele doua conditii (10.59) si (10.60) sunt satisfacute pe orice element finit de suprafata. În plus, formula lui Kirchhoff (10.72) nu reproduce conditiile la limita precizate, daca se aduce punctul P pe suprafata (S).

10.4.2. Teoria lui Sommerfeld

Inconsistentele matematice ale teoriei lui Kirchhoff sunt evitate daca în locul functiei auxiliare φ, relatia (10.66), se aleg functii Green adecvate conditiilor la limita (de frontiera) pe suprafata considerata.

Astfel, daca pe suprafata (S) functia ψ este cunoscuta sau aproximata, atunci este necesar a se introduce o functie Green de tip Dirichlet G_D(r) care satisface conditia:

G_D=0; pe suprafata (S). (10.78)

În acest caz, o integrala Kirchhoff generalizata, echivalenta cu (10.72) este:

(10.79)

iar o aproximatie consistenta este ψ=0 pe ecranele opace si ψ=ψ₀ (corespunzator undei incidente în propagare libera) în aperturi.

Daca este aproximata sau cunoscuta derivata normala a functiei ψ pe suprafata (S), atunci se foloseste o functie Green de tip Neumann G_N(r) care verifica conditia:

pe suprafata (S). (10.80)

Integrala Kirchhoff generalizata, echivalenta cu (10.72) pentru conditiile Neumann pe suprafata de frontiera este:

. (10.81)

si în acest caz, poate fi formulata o schema consistenta de aproximare.

Sommerfeld utilizeaza pentru studiul difractiei luminii în aproximatia scalara (optica) functia Green definita prin conditiile:

ΔG+k²G=0 în volumul (V_S), (10.82)

G=0 pe suprafata (S), (10.83)

când si (10.84)

când , (10.85)

unde r=PM (fig.10.23).

Functia Green definita de conditiile (10.82-85) difera de solutia sferica (10.66) prin conditia (10.83) si se reduce la ea când r tinde la zero, conform conditiei (10.84). Conditia (10.85) se numeste conditia de radiatie sau ecuatia telegrafistilor si este specifica undelor.

Se constata ca Sommerfeld alege o functie Green de tip Dirichlet, iar perturbatia luminoasa în punctul P este data de integrala (10.79) cu conditiile la limita (pe suprafata de frontiera (S)):

ψ=ψ₀ pe aperturi si ψ=0 pe ecranele opace. (10.86)

Conditiile de frontiera (10.86) sunt compatibile din punct de vedere matematic, iar teoria lui Green asigura ca valorile (10.86) vor fi reproduse de functia ψ când punctul P se afla pe suprafata (S). Din punct de vedere fizic, conditiile (10.86) nu reprezinta decât într-o prima aproximatie fenomenele de difractie, deoarece câmpul electromagnetic nu este independent de prezenta marginilor aperturilor din ecran.

Problema se reduce acum la determinarea expresiei functiei Green care satisface conditiile impuse. Cazurile în care aceasta functie se poate determina sunt putine si implica existenta unor geometrii simple.

Un asemenea caz, important din punct de vedere experimental, este cel în care suprafata ecranului prevazut cu apertura σ este plana si infinita, fig.10.26. În acest caz, functia Green se construieste utilizând metoda imaginilor; punctul P' fiind imaginea în planul (S) a punctului de observatie P. Pentru punctul recurent se formeaza functia Green pentru conditii Dirichlet:

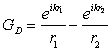(10.86)

Daca se adoptau conditii Neumann, functia Green trebuia aleasa de forma:

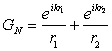
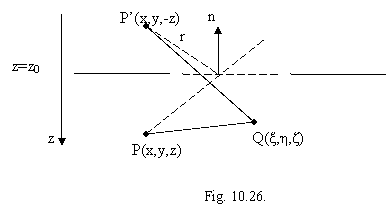
Functia Green (10.86) satisface conditiile (10.82-85); singularitatea acestei functii în punctul imagine P' nu violeaza aceste conditii, întrucât punctul P' se afla în semispatiul z>0 în care nu se aplica teorema lui Green (în regiunea surselor).

Cum:

, (10.87)

unde:

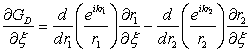, (10.88)

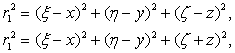
daca punctul arbitrar Q se afla pe apertura (se confunda cu M):

r₁=r₂=r

si:

rezulta:

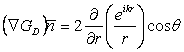. (10.89)

Cum, în general, r>>λ se aproximeaza:

(10.90)

si atunci din (10.89),(10.90) înlocuind în (10.79) se obtine:

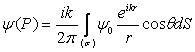, (10.91)

daca se tine cont de conditiile (10.86).

În fine, daca unda incidenta este sferica , înlocuind în (10.91) rezulta:

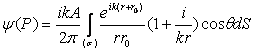. (10.92)

Riguros, daca nu se face aproximatia (10.90), perturbatia luminoasa în punctul P este:

(10.93)

care are o forma analitica relativ simpla, constituind punctul de plecare pentru cele mai multe cazuri de calcul explicit din difractia optica.

De altfel, din compararea relatiilor (10.76) si (10.92) în teoria lui Huygens si respectiv, în teoria lui Sommerfeld pentru o unda incidenta sferica se constata o foarte buna concordanta, deosebirea privind numai factorulde oblicitate.

10.5. Principiul lui Babinet

Principiul lui Babinet leaga câmpurile de difractie ale unui ecran difractant de cele ale ecranului complementar. Astfel daca pe suprafata (S) a unei geometrii de difractie exista o repartitie data de paravane opace (p) si aperturi, perturbatia luminoasa în punctul de observatie P se calculeaza prin relatia:

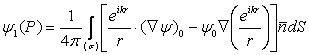(10.94)

în cazul teoriei lui Kirchhoff,

(10.95)

în cazul teorie lui Sommerfeld pentru conditii Dirichlet si respectiv:

(10.96)

în cazul teoriei Sommerfeld pentru conditii Neumann.

Daca se presupune acum ca pe suprafata (S) locul ecranelor opace este luat de aperturi, iar locul aperturilor de ecrane opace (o astfel de "permutare" definind ecranele complementare), atunci perturbatia luminoasa în punctul de observare P este ψ₂(P), care se evalueaza tot din integralele (10.94),(10.95) sau (10.96) numai ca acum domeniul de integrare este (Π).

În aceste conditii, conform principiului lui Babinet, câmpurile de difractie observate cu ecrane complementare se aduna pentru a da câmpul în cazul când nu exista ecrane, adica:

Ψ(P)=Ψ₁(P)+Ψ₂(P).

Formularea riguroasa a principiului lui Babinet este data de teoria electromagnetica, vectoriala a difractiei.