Energia si fortele electrostatice

1.10.1. Energia electrostatică

Pentru a stabili un câmp electrostatic este nevoie de un lucru mecanic. Energia acestui câmp electrostatic este egală cu lucrul mecanic ce trebuie efectuat pentru aducerea sarcinilor din exterior în pozițiil 18218o1412s e pe care le ocupă în câmp. Operațiunea aceasta trebuie făcută lent și izoterm pentru a avea mereu echilibru electrostatic. Dacă la un anumit moment sarcina corpului K este q_k, ea reprezintă o fracțiune din valoarea ei finală și deci:

(1.87)

Potențialele corpurilor variază liniar cu sarcinile și deci potențialul V_k al corpului K la un moment dat este:

Mărimea ia valori între zero și unu. Pentru mărirea sarcinii unui corp cu cantitatea dq_k trebuie ca forțele exterioare să efectueze un lucru mecanic pentru a învinge forțele câmpului. Dacă este intensitatea câmpului electric, acesta exercită asupra sarcinii forța elementară iar forța exterioară trebuie să fie: .

Prin urmare lucrul mecanic elementar efectuat de forțele exterioare pentru creșterea sarcinii fiecărui corp cu , este: 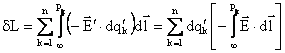(1.88)

dar este potențialul V_k al corpului în momentul respectiv și deci,

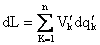(1.89) Energia câmpului a crescut deci, cu mărimea: (1.90) Ținând seama că și , iar , rezultă:

. (1.91) Energia finală se obține prin integrare: 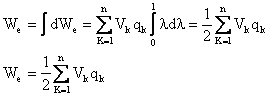(1.92)

relație ce constituie expresia energiei unui sistem de corpuri încărcate.

Pentru un condensator plan, energia înmagazinată între armături este dată de relația:

. (1.93) Pentru a arăta că energia este localizată în câmpul electric al condensatorului o vom exprima în funcție de mărimile și . Pornind de la relațiile:

. (1.94)

Rezultă: (1.95)

unde V=S d. este volumul dielectricului dintre armături. Se introduce astfel noțiunea, densitate de volum a energiei electrice definită astfel: (1.96)

în câmpurile omogene și:

în câmpurile neomogene. Cunoscând densitatea de volum se poate stabili energia sistemului cu relația:

(1.97)

1.10.2. Forțele electrostatice și teoremele forțelor generalizate

Fie un sistem de corpuri încărcate și presupunem că unul dintre ele se deplasează, variind astfel una din coordonatele sale generalizate. Lucrul mecanic efectuat de forțele exterioare pentru a varia cu dq_k sarcina, conductoarele trebuie să compenseze atât creșterea de energie a câmpului, cât și lucrul mecanic efectuat de forța generalizată (moment, forță, presiune, etc.). Bilanțul energetic al unui sistem de corpuri încărcate, este: 

(1.98) Se deosebesc două cazuri particulare în acest proces: - potențialele corpurilor se păstrează constante; - sarcinile corpurilor se păstrează constante.

Teorema I Când sarcinile sunt constante, rezultă dq_K =0 și relația (1.98) conduce la:

(1.99) Acest caz corespunde situației când corpurile încărcate cu sarcini sunt deconectate de la surse și sunt înconjurate numai de dielectrici. Relația (1.99) reprezintă prima teoremă a forțelor generalizate.

Semnul (-) se interpretează prin aceea că dacă X și dx sunt de același sens energia sistemului scade. Într-adevăr dacă sursele sunt deconectate, deplasarea corpurilor se produce numai pe seama energiei interne a sistemului și deci această energie va scădea. Teorema a-II-a Dacă potențialele sunt constante (V_k=ct) relația (1.92) devine: (1.100)

care introdusă în (1.98) conduce la: . (1.101) Aceasta este cea de-a doua teoremă a forțelor generalizate și corespunde situației când sistemul este conectat la surse (V=ct) și deci deplasarea corpurilor are loc pe seama unui consum de energie de la sursă. De remarcat faptul că atât relația (1.99) cât și (1.101) conduc la același rezultat.

Cu teoremele forțelor generalizate, forța de atracție dintre armăturile unui condensator plan este: 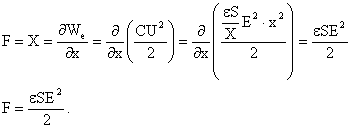(1.102)

Aplicația 1 Un condensator plan are suprafața , iar distanța dintre armături d=6mm. Între armături se aplică o tensiune U=6kV. Să se calculeze capacitatea condensatorului C, intensitatea câmpului electric E și energia W_e a condensatorului în ipotezele:

a) - dielectric este aerul: e_r=1; b) - dielectric este uleiul de transformator: e_r c) - dielectricul este format dintr-o placă de sticlă groasă de 4mm (e_r=6) și restul intervalului este acoperit cu un strat de parafină (e_r

Rezolvare:  a.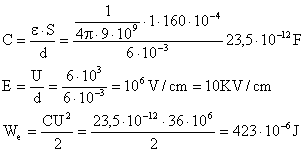

b. 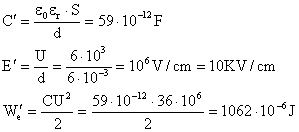c. Se formează două condensatoare în serie C₁" și C₂". Rezultă: ,

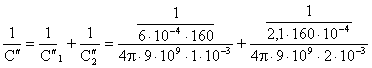deci:

Aplicația 2

Un condensator plan, cu armături circulare, paralele cu raza r = 8cm și distanța dintre armături d=2mm, având ca dielectric uleiul de transformator (), este supus la o tensiune constantă U =100V. Să se calculeze:

a. Forța de atracție dintre armăturile condensatorului;  b. Intensitatea câmpului electric dintre armături; c. Energia necesară pentru a deplasa armăturile la distanța d = 6mm.

Rezolvare 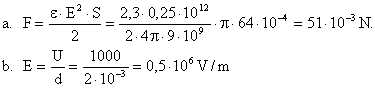c. Lucrul mecanic ce se efectuează este:
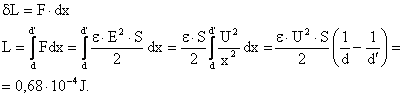