NOTIUNI SUMARE DE TEORIA ELASTICITATII
TEORIA TENSIUNILOR
ECUATILE DIFERENTIALE DE ECHILIBRU
(SI DE MISCARE) ALE LUI NAVIER-CAUCHY.
ASPECTUL STATIC
1. Pentru inceput vom face cateva precizari de notatii ale
tensiunilor, astfel incat sa poata fi usor de manuit in cazul problemelor spatiale si sa permita o
distinctie clara intre tensiunile de pe sectiuni diferite duse prin acelasi
punct al unui corp solicitat.
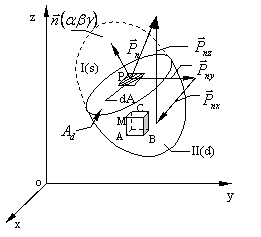Astfel, sa ne imaginam un corp solid
(continu) deformabil si sa ducem prin punctul P din interiorul lui un plan de
sectionare arbitrar (fig.1.1.1), care-l imparte in doua. Sa inlaturam partea I(s); in planul sectiunii sa izolam in
jurul punctului P un element de suprafata dA. Caracterizam acest element de
suprafata ca orientare spatiala prin normala exterioara 
exterioara in raport cu partea ramasa II(d)
care face unghiurile
cu
axele unui triedru ortogonal (xOyz) (arbitrar) cu ajutorul normalei exterioare
se indica simplu nu numai orientarea suprafetei, dar si partea corpului care se
inlatura dupa sectionare si a carei actiune se inlocuieste prin forte interioare.
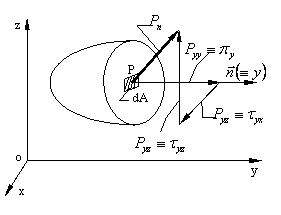
Sa notam cu 
tensiunea totala din punctul P; ea este
rezultanta fortelor interioare care actioneaza pe elementul de suprafata dA.
Proiectiile pe axele de coordonate ale acestui vector le vom nota cu 
.
De obicei, in Rezistenta materialelor, se lucreaza cu componentele normale(
)
si tangentiala(
)
ale acestui vector. Cum componentele introduse de noi nu sunt in general orientate nici dupa normala
nici dupa tangenta la planul de sectionare,
vom incerca sa le descompunem in continuare. Pentru aceasta sa presupunem ca
planul de sectionare il luam perpendicular pe una din axele de
coordonate(figura 1.1.2)- de exemplu pe axa y. Deoarece normala este orientata dupa axa y, proiectiile
tensiunii totale vor fi 
In mod similar facand sectiuni perpendiculare pe celelalte axe se obtin componentele:
Se vede
imediat ca tensiunile 
pentru care cele doua litere de la indici sint
identice reprezinta tensiuni normale; dupa uzanta din Rezistenta materialelor
ele se vor nota cu 
Celelalte sase componente sunt tensiuni
tangentiale actionand in aceleasi suprafete , normale pe axele de coordonate,
avand primul indice identic cu al tensiuni normale.
Sa mai facem cateva
consideratii globale asupra varietatii tensiunilor de la un punct la altul.
Pentru aceasta, intr-un punct arbitrar M(xyz) din interiorul corpului sa
consideram un element de suprafata dA perpendicular pe axa y(de exemplu);
tensiunile care lucreaza pe acest element(deci in punctul M) vor fi 
Consideram punctul M*(x+dx,
y+dy, z+dz) infinit apropiat de punctul M, prin care ducem un element de
suprafata de asemenea perpendicular pe axa y; tensiunile(
)
vor diferi de componentele respective ale tensiunilor din punctul M cu marimi
infinit mici. Aceasta afirmatie se bazeaza pe principiul ca in cazul unui mediu
continuu tensiunile sunt functii continue de punct
;etc. (1.1.1)
In aceasta situatie componentele tensiunilor din punctul M* se pot exprima cu ajutorul tensiunilor din punctul M, dezvoltand functiile(1.1.1) in serie Taylor si neglijand infinitii mici de la ordinul doi in sus:
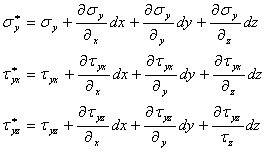(1.1.2)
Daca punctele M si M* se gasesc pe directii paralele cu una din axe, relatiile(1.1.2) obtin forme mai simple.
Ne propunem acum sa studiem cum variaza starea de tensiune dintr-un punct arbitrar M al unui corp solicitat la trecerea intr-un punct infinit apropiat M*. Pentru aceasta din jurul punctului M(v.fig. 1.1.1) vom izola un paralelipiped infinit mic de laturi dx, dy, dz. Fetele acestui paralelipiped de muchii MA, MB, MC(care se intalnesc in punctul) le vom considera ca plane fundamentale si le vom alege drept plane de coordonate. Desenam marit acest element de volum(fig.1.1.4) si figuram tensiunile care actioneaza pe fetele lui.x)
La trecerea de
la o fata la lata tensiunile variaza cu cantitati infinit mici de forma celor
date de relatiile(1.1.2). De exemplu, daca variaza numai coordonata x(cu dx),
tensiunea
va deveni
(deoarece
dy dz
x) Sa observam ca oricat de mici ar fi dimensiunile fetelor paralelipipedului elementar, tensiunile de pe aceste fete pot fi distribuite neuniform. De aceea vom considera ca toate tensiunile reprezentate pe fig. 1.1.4 sunt de fapt niste valori medii.
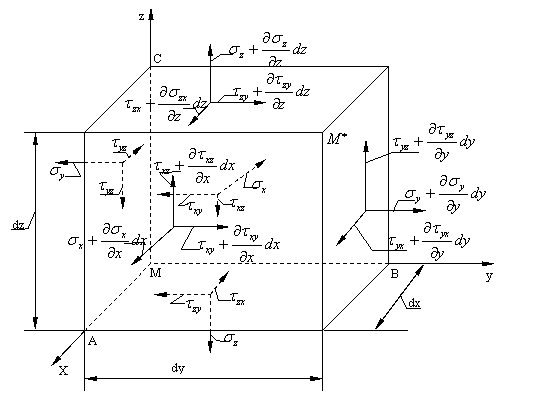
Pentru a studia echilibrul acestui element de volum sa mai precizam care sunt fortele elementare ce actioneaza asupra lui
-in primul rand fortele interioare, devenite prin aplicarea metodei sectiunilorforte exterioare, care sunt date de produsul dintre tensiune aria suprafetei elementare pe care lucreaza aceasta tensiune:
-in al doilea rand vom presupune ca in corpul dat avem asa numitele forte masice" sau forte de volum de tipul fortelor gravitati 242g62c onale. Vom nota cu X, Y, Z componentele fortelor masice care actioneaza asupra unitatii de volum.
Vom presupune corpul dat in echilibru (static sau dinamic): atunci pentru fiecare paralelipiped elementar in parte trebuie sa fie satisfacute sase ecuatii de echilibru static:
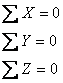
(1.1.3)
Observatie. Daca corpul se
afla in miscare, membrul din dreapta al ecuatiilor de proiectii nu este nul:
conform legii a doua a lui Newton trebuie sa fie egal cu proiectia fortei de
inertie pe axa respectiva(adica, cu produsul dintre masa elementului si
proiectia acceleratiei sale pe axa considerata). Daca vom nota cu u, v, w
proiectiile deplasarii punctului M dupa cele trei axe, atunci proiectiile
acceleratiei se scriu
.De
aceea in partea dreapta a primelor trei ecuatii (1.1.3) se vor adauga expresii
de forma:
(1.1.4)
Daca explicitam prima
ecuatie de echilibru 
obtinem
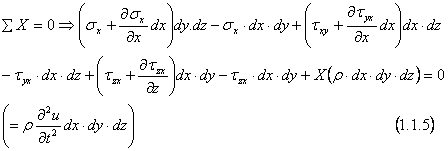
Se reduc termenii asemenea si se simplifica
cu 
.
Explicitam analog si celelalte doua ecuatii de proiectii si obtinem in final
ecuatiile:
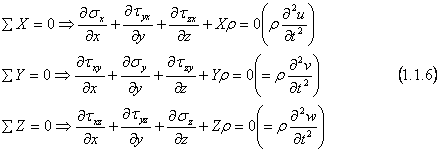
Aceste relatii sunt cunoscute sub numele de "ecuatiile diferentiale de echilibru ale lui Navier-Cauchy".
Sa trecem acum la explicitarea ultimelor trei
ecuatii de echilibru din(1.1.3). Sa luam ecuatia
,
care ne da:
Vom observa ca unele momente vor fi infiniti mici de ordinul trei, iar altele de ordinul patru. De exemplu pentru tensiunile normale de pe cele doua fete laterale perpendiculare pe axa y, avem(v.fig.1.1.4)
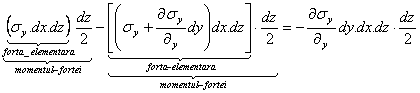
Acest moment este de fapt o marime infinit
mica de ordinul patru: de acelasi ordin de marime sunt si momentele fortelor
masice:
Atunci
, neglijand infinitii mici de ordinul patru si reducand termenii asemenea, se
obtine:
Am obtinut cunoscuta lege a dualitatii sau a reciprocitatii tensiunilor tangentiale. Celelalte doua ecuatii de momente ne conduc la relatii similare:
(1.1.9)
Deci, conditiile de echilibru static ne conduc la trei
ecuatii diferentiale(1.1.6) care contin noua functii (necunoscute) de
coordonatele punctului 
Dar legea dualitatii
tensiunilor tangentiale(1.1.8): (1.1.9) ne arata ca de fapt ultimele sase
functii sunt egale doua cate doua. Rezulta ca in realitate avem numai trei
ecuatii diferentiale cu sase functii necunoscute:
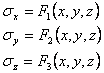
Deoarece numarul functiilor necunscute (sase) depaseste numarul ecuatiilor (trei), studiul static al problemei este insuficient pentru determinarea celor sase functii(1.1.10). Asta inseamna ca "problema teoriei elasticitatii este triplu static nedeterminata" . Ecuatiile suplimentare de care avem nevoie le vom obtine din studiul deformatiilor care se oproduc in corp (aspectul geometric) si din relatiile dintre deformatii si tensiuni care exprima proprietatile fizice ale corpului elastic dat(aspectul fizic
Integrarea ecuatiilor diferentiale va arata forma functiilor pe care le cautam: insa procesul de integrare conduce la aparitia unor constante arbitrare respectiv a unor functii nedeterminate, pe care pentru ale afla va trebui sa utilizam anumite conditii al limita(conditii pe suprafata sau pe contur) care stabilesc relatia dintre fortele interioare si fortele exterioare aplicate pe suprafata corpului.
1.2 Tensorul tensiunilor. Tensiuni in sectiuni
inclinate. Conditii la limita
Ne propunem sa studiem starea de tensiune dintr-un punct dat al unui corp solid deformabil solicitat, aflat in echilibru. Dupa cum stim, a cunoaste starea de tensiune din acest punct inseamna a cunoaste tensiunile (normale si tangentiale) care lucreaza pe infinitatea de elemente de suprafata care se pot duce prin punctul respectiv. Vom demonstra insa ca pentru aceasta este necesar si suficient sa cunoastem numai tensiunile de pe trei elemente de suprafata triortogonale care trec prin punctul respectiv.
Urmand aceasta idee, vom alege un sistem de axe rectangulare cu originea in punctul constant(M) si vom izola un element de volum infinit mic sub forma unei piramide triunghiulare elementare(MABC) cu varful in punctul M si cu baza obtinuta cu ajutorul unui plan inclinat arbitrar, infinit apropiat de punctul M, care intersecteaza toate cele trei axe de coordonate (fig1.2.1).
Sa presupunem ca ne sunt date tensiunile normale si tangentiale care lucreaza pe fetele acestei piramide cuprinse in planele de coordonate: ne propunem sa determinam tensiunile care lucreaza pe suprafata inclinata ABC.
Problema poate fi formulata si putin altfel: sa presupunem ca decupam (izolam) din jurul punctului M paralelipipedul infinit mic prezentat in paragraful precedent (v.fig 1.1.1 si 1.1.4) si ca se cunosc tensiunile normale si tangentiale de pe trei fete ortogonale paralele cu planele de coordonate: ni se cere sa determinam tensiunile pe un plan oarecare inclinat in raport cu fetele paralelipipedului, sau altfel spus pe un plan "oblic" care trece prin interiorul paralelipipedului(fig.1.2.2)
Sa notam (V.fig 1.2.1)
Suprafata fetei inclinate ABC cu dA,
Normala exterioara la
aceasta fata cu :
unghiurile pe care aceasta normala le face cu axele de coordonate cu 
,
;
Tensiunea totala care
actioneaza pe suprafata dA cu.
Aceasta poate fi descompusa fie dupa cele trei axe de coordonate in pnx',
pny', pnz' fie dupa normala (obtinind componenta normala 
) si dupa o directie
perpendiculara pe normala cuprinsa in planul suprafetei ABC (obtinand
componenta tangentiala 
Suprafetele celorlalte fete se vor
gasi proiectind suprafata dA pe planele de coordonate, deci:
Scriem conditile de echilibru (de tipul
1.1.3) pentru aceasta piramida elementara.Sa explicitam prima ecuatie Se obtine:
(1.2.2)
Tinand cont de (1.2.1), simplifinind cu dA si explicitind si celelalte ecuatii de proiectii rezulta in final:
(1.2.3)
Aceste ecuatii ne spun ca proiectile pe axe ale tensiuni totale sunt functii lineare de cele noua componente ale starii de tensiune. De aici
(1.2.4)
In aceste ecuatii nu au intrat fortele masice si nici
termenii care repreznta fortele de inertie, deoarece sunt infiniti mici de
ordinul al treilea (de ex.:
) in
timp ce toti ceilalti termini ai ecuatiei (1.2.2) - in aceasta forma initiala -
sunt infiniti mici de ordinul doi. Situatia este analoaga ii pentru termenul
care exprima forta de inertie cind corpul se afla in miscare; din acleasi
considerente stiind relatiile de tipul (1.2.2) nu am introdus nici o crestere
tensiunilor.
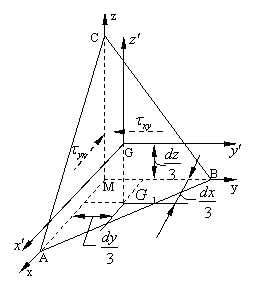
5. Pentru a usura scrierea ecuatiilor
de momente alegem un sistem de axe paralel cu primul cu originea in centrul de
greutate al suprafetei inclinate dA
remarcam ca coordonatele noii origini (G) sunt (
), iar
proiec tiile acestui punct pe planele de coordonate sunt tocmai centrele de
greutate ale suprafetelor laterale MAB, MAC, MBC ale piramidei(fig.1.2.3). In
acest caz nu toate componentele tensiunilor mari dau momente; de exemplu, daca
vrem sa scriem ecuatia de momente in raport cu axa z', nu produc momente decat fortele
elementare 
-toate
celelalte forte elementare au momente nule(fig1.2.3) rezulta explicit:
Deci 
.Am
obtinut din nou relatia care exprima principiul dualitatii tensiunilor
tangentiale. Din celelalte ecuatii de echilibru se obtin relatii similare:
.
Concluzii
I. In relatiile(1.2.3) nu au intrat dimensiunile piramidei
elementare si nici distanta de la punctul considerat M, in care studiem starea de tensiune a corpului (ales ca origine a
axelor de coordonate) pana la suprafata inclinata. Aceasta ne permite sa
afirmam ca, daca dimensiunile piramidei sunt infinit de mici, suprafata inclinata dA trece chiar prin
punctul M. Inseamna ca utilizand relatiile(1.2.3), daca se cunosc
tensiunile normale si tangentiale de pe trei elemente de suprafata care trec
prin punctul M, putem determina tensiunile de pe oricare element de suprafata
de normala 
care
trece prin acest punct. Rezulta ca starea de tensiune dintr-un punct al unui
solid deformabil solicitat este complet determinata de ansamblul tensiunilor
care lucreaza pe trei elemente de suprafata ortogonale ce trec prin acest
punct. Acest ansamblu de tensiuni este format din sase marimi independente:
,
care se numesc componentele starii de tensiune din punctul M.
II. Daca se studiaza transformarea componentelor starii de tensiune la o rotire arbitrara a sistemului de coordonate, se obtine niste relatii de tipul:
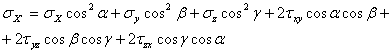
etc. (1.2.4)
Nu demonstram aceste relatii, deoarece pentru noi au numai o importanta teoretica principala; ele ne arata ca starea de tensiune dintr-un punct al unui corp solicitat este o marime fizica speciala, reprezentand o generalizare a notiunii de vector, numita marime tensoriala. Aceasta marime se numeste in mecanica solidului deformabil, tensorul tensiunilor notat:
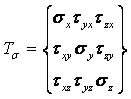(1.2.5)
, iar
tensiunile din planele de coordonate sau componentele starii de tensiune se
numesc componentele tensorului. Fiecare coloana verticala a tensorului
este
formata din componentele tensiunii totale de pe unul din planele de coordonate;
fiecare rand orizontal este format din tensiunile de pe planele de coordonate
paralele cu una din axele de coordonate. Sa remarcam ca adoptarea unei asemenea
forme de notare a tensorului tensiunilor nu trebuie sa duca la ideea ca el
poate fi tratat ca un determinant sau ca o matrice.
Datorita proprietatii de dualitate a
tensiunilor tangentiale componentele tensorului dispuse simetric fata de diagonala
principala(diagonala care trece prin tensiunile normale )
sunt egale intre ele; de aceea el reprezinta ceea ce se numeste un tensor
simetric de ordinul al doilea. Comparatia cu vectorii ne este de multe ori
utila pentru intelegerea sensului fizic al acestor marimi tensoriale. De
exemplu o marime vectoriala, care poate fi considerata ca un tensor de ordinul
intai , este univoc determinata de trei marimi scalare care in cazul nostru
determina starea de tensiune dintr-un punct al corpului si sunt tensiunile
normale si tangentiale din trei plane de coordonate care trec prin acel punct.
Mai mult, noi stim ca in cazul miscarii unui corp, viteza oricarui punct al sau
este un vector care nu depinde de sistemul de coordonate in acre este studiata
miscarea corpului, desi prioritatile sale sunt diferite in diferite sisteme de
coordonate. In mod similar si starea de tensiune intr-un punct al unui corp
este o marime fizica independenta de alegerea axelor de coordonate.
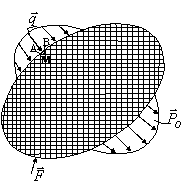
III. Conditii la limita. Divizarea corpului in
paralelipipede elementare nu este posibila i, totalitate, deoarece pentru cazul
general al unui corp de forma oarecare elementele de volum din imediata
vecinatate a suprafetei nu mai pot avea o asemenea forma, fig 1.2.4 de aceea
cazul pe care l-am studiat al piramidei elementare ne ajuta sa rezolvam si
aceasta situatie.Mai mult, cu ajutorul acestor forme de elemente de volum 
putem sa stabilim relatiile
dintre fortele de suprafata sau sarcinile exterioare aplicate corpului si fortele
interioare sau tensiunile care lucreaza pe plane paralele de coordonate, din
imediata vecinatate a suprafetei inclinate apartinand suprafetei exterioare a
corpului.Aceste relatii reprezinta chiar conditiile la limita sau conditiile pe
suprafata cautata. In aceasta ordine de idei sa decupam tetraedrul elementar
MABC astfel incat fata ABC sa apartina suprafetei corpului. Atunci proiectiile
fortelor exterioare raportate la unitatea de suprafata (notate cu 
)
vor reprezenta tocmai proiectiile vectorului tensiunii totale pnx,pny,pnz
care lucreaza pe suprafata inclinata ABC. Putem scrie in aceasta acceptiune:
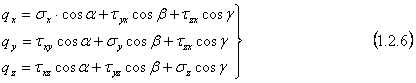
Deci, aceste relatii stabilesc legatura dintre sarcina exterioara si fortele interioare reprezentand ceea ce vom numi conditii la limita sau conditii pe suprafata corpului. Ele sunt strans legate de ecuatiile diferentiale de echilibru ale lui Navier-Cauchy(1.1.6). In adevar, daca functiile F1.F6(1.1.10) sunt astfel alese incat ecuatiile diferentiale si conditiile la limita sunt satisfacute in toate punctele din interiorul corpului cat si pe suprafata sa, atunci echilibrul tuturor elementelor de volum - paralelipipede si tetraedre - in care am divizat corpul este asigurat si deci va fi asigurat si echilibrul corpului in ansamblu. Sensul matematic ala acestei concluzii este legat de faptul ca ecuatiile diferentiale (1.1.6) si conditiile la limita(1.2.6) trebuiesc studiate impreuna, deoarece aceste ecuatii nu pot avea o solutie determinanta(unica) atat timp cat conditiile la limita, cuprinzand solicitarile exterioare ale corpului, nu sunt date("problema tip Cauchy"). Am demonstrat astfel ca ecuatiile(1.1.6) si conditiile la limita(1.2.6) sunt suficiente pentru echilibrul corpului sub actiunea fortelor exterioare date. Utilizand o transformare Green se poate arata ca aceste conditii sunt si necesare
IV. De cele mai multe ori tensiunea
totala pn care actioneaza pe elementul de suprafata inclinat ABC cu
normala se descompune intr-un vector orientat dupa
normala (componenta
normala a tensiunii totale:)
si altul cuprins in planul sectiunii(componenta tangentiala a tensiunii totale:).
Deoarece nu cunoastem unghiul pe care-l face directia tensiunii totale cu normala ,
vom folosi componentele dupa cele trei axe ale acestei tensiuni: deci
(utilizand si1.2.3):
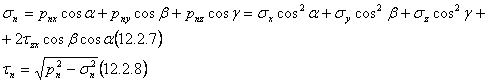
(componenta tangentiala se determina numai ca marime nu si ca semn: pn2 este dat de 1.2.4):
TEORIA GEOMETRICA A DEFORMATIILOR
1.3. RELATIILE DIFERENTIALE DINTRE COMPONENTELE DEFORMATIEI
SI COMPONENTELE DEPLASARII UNUI PUNCT
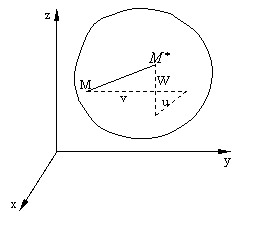
1. Sa consideram un corp solid deformabil oarecare,
astfel fixat in spatiu incit sa nu fie posibila deplasarea sa ca slid rigid. Totusi,
sub actiunea fortelor exterioare, diferitele puncte materiale ale corpului
sufera deplasari ca urmare a procesului de deformare de ansamblu a corpului.
Astfel
sa studiem un punct material oarecare M(x, y, z) din corp (fig1.3.1). In urma
deformarii corpului punctul M se va deplasa in pozitia M*; vectorul 
reprezinta
deplasarea totala a punctului M.
Proiectiile acestui vector pe
axele de coordonate le vom nota cu: u,v,w, si le vom numi componentele deplasarii
starii totale a punctului M". cum diferitele puncte ale corpului vor avea in
general deplasari diferite, rezulta ca deplasarile unui punct (mai exact
componentele deplasarii totale) vor fi functii de coordonatele punctului
(functii de punct):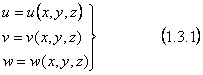
Sa
consideram acum, la o distanta infinit mica fata de punctul M, un alt punct N
ale carui coordonate inainte de deformatie au fost: x+dx, y+dy, z+dz; dupa
deformatia corpului punctul N ocupa poyitia N* (fig..); componentele deplasarii
totale 
pe
care le vom nota cu u* v* w*, se pot scrie cu o exactitate satisfacatore,
dezvoltind in serie Taylor in jurul punctului M, functiile (1.3.1):
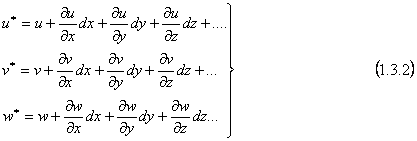
Interpretarea analitica este evidenta daca presupunem ca deplasarea totala a unui punct este o functie totala de punct; asta inseamna ca si componentele deplasarii (1.3.1); sunt functii continue de punct. Ele pot fi deci dezvoltate in serie Taylor, in care se neglijeaza infinitii mici de ordin superior in contextul acceptarii premi zelor teoriei clasice a elasticitatii, in particular a ipotezei micilor deplasari.
In analiza pe care o facem ne intereseaza mai mult niste forme particulare ale relatiilor (1.3.2). De exemplu, daca ambele puncte se gasesc pe o dreapta paralela cu oricare din axe, modul de scriere a componentelor deplasarii punctului vecin se simplifica.
Astfel, daca punctele M si N se gasesc intr-un plan paralel cu planul de coordonate xoy, iar dreapta MN este paralela cu axa ox, atunci dy=dz=0 si prin urmare;
(1.3.3)
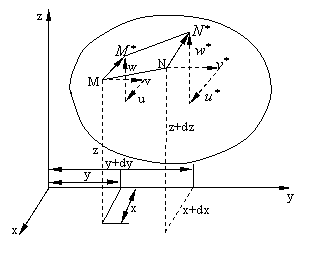
3. Sa trecem acum de la deplasari la deformatii si sa
izolam din corpul elastic studiat, din jurul punctului M un paralelipiped
infinit mic de muchii dx, dz, dz cu ajutorul unor plane de coordonate. Un
astfel de element de volum a fost deja studiat de ni din punct de vedere
static. Acum insa vom lua in considerare faptul ca in urma deformatiei corpului
acest element de volum se va deplasa si se va deforma adica muchile sale isi
modifica lungimea, concomitent cu variatia unghiurilor care initial erau niste
triedre sau driedre drepte.
Pentru determinarea
deformatiei corpului elastic in punctul M, ca trebui deci sa studiem lungirea
muchiilor (deformatiile lineare) dx, dy, dz ale paralelipipedului precum si modificarea unghiurilor dintre
aceste muchii 1M2; 1M3; 2M3 (ceea ce am denumit lunecari sau deformatii
unghiulare). Deoarece studierea deformatiei in ansamblu, a paralelipipedului,
este a problema mai dificila, vom studia separat deformatiile proiectiilor
acestuia pe planele de coordonate (Fig.1.3.3); cunoscand deplasarile si
deformatiile celor trei proiectii vom putea determina, evident si deformatiile
paralelipipedului in ansamblu.
Sa onsideram de exemplu proiectia elementului de volum M123 pe planul xoy, reprezentata de dreptunghiul ABCD (Fig.1.3.4) Pana la deformatie lungimile muchiilor au fost AB=dx si BC=dy.
Dupa deformare,
acest element de suprafata (de data aceasta) sufera atato deplasare cat si o
deformare. Ne putem imagina pozitia finala deformata a elementului (A1B3C3D3)
suprapu nand o succesiune de deplasari si deformatii; de exemplu, elementul
ABCD sufera pentru inceput o deplasare de vector total AA1
(componentele deplasari u,v), dupa care muchiile sale se lungesc (sau se scurteaza) elementul trecand in pozitia
A1B2C2D2; deformatiile unghiulare
se manifesta prin rotatiile muchiilor, cu unghiurile 
elementul ocupand in final pozitia A1B3C3D3.
Sa analizam putin urmarind fig.1.3.4 notatiile si valorile deplasarilor diferitelor uncte ale elementului ABCD.
Punctul
A(x,y) trece in pozitia A1; vectorul AA1 reprezinta
deplasarea totala a punctului A iar componentele sale dupa axele x si y le
notam cu c si v.
Punctul B (x+dx, y) se gaseste pe o dreapta paralela cu axa ox, deci dy=0; el ocupa in final pozitia B3, deci vectorul BB3 reprezinta deplasarea totala a punctului B. Componentele acestei deplasari, repreyentate de segmentele BE si EB3 sunt legate de componentele deplasarii punctului A prin relatii de tipul (1.3.2) si ele sunt (dy=0):
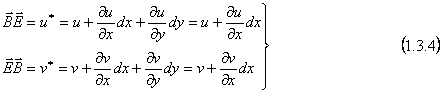
In mod analog deplasarea punctului D(x, y+dy) care se gaseste pe o muchie paralela cu axa y (deci dx=0) este data de vectorul DD3 ale carei componente sunt;
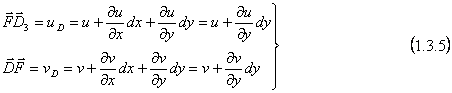
Am prezentat foarte detailat modul de acriere a acestor componente de deplasari, deoarece de multe ori scrierea si intelegerea lor se face cu dificultate si eronat. Atragem atentia asupra acestui rationament.
6. Deacum incolo calcul este evident. Lungirea specifica a muchiri AB, a carei lungime initiala a fost dx, se scrie cu o aproximatie ce merge pana la infinitii mici de ordinul intai:
In mod analog pentru lungirea specifica in lungul axei oz, avem:
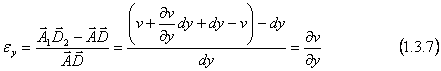
Pe aceeasi cale, atudiind deformaatiile proiectiilor de pe celelalte plane de coordonate, vom obtine:
7. Sa trecem acum la analiza
deformatiilor unghiulare. Pentru unghiul de rotire al muchiei Ab in planul xoy
notat cu 
Avem evident;
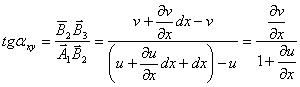
Deoarece ne-am limitat la cazul
deformatiilor mici, la numitorul expresiei precedente putem neglija lungirea
specifica 
care este mult mai mica in comparetie cu
unitatea 
si vom obtine :
(1.3.9)
In mod asemanator vom obtine unghiul
de rotatie al muchiei 
:
Cum:
(1.3.10)
Prin definitie lunecarea specifica (sau deformatia specifica unghiulara) in planul xoy, reprezinta unghiul total cu care se modifica unghiul drept initial BAD, deci:
(1.3.11)
Prin permutati circulare, putem exprima si lunecarile specifice din celelalte plane de coordonate.
Obtinem in final sase relatii diferentiale care caracterizeaza deformatia intr-un punct al unui corp numite uneori ecuatiile geometrice ale lui Cauchy:
Deformatii specifice liniare Deformatiile specifice unghiulare
(lungimile specifice) (lunecarile specifice)
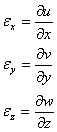
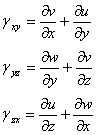(1.3.12)
8. Concluzii.
Ecuatiile diferentiale de echilibru (1.1.6) si ecuatiile geometrice (1.3.12)
formeaza inpreuna un sistem de 9 ecuatii diferentiale 15 necunoscute (
).
Prin urmare, pentru rezolvarea complecta a problemei propuse, la cele doua
grupari de exercitii, pe care le-am obtinut deocamdata, mai trebuie sa adaugam
inca 6 ecuatii, cu conditia evidenta ca acestea sa nu mai introduca necunoscute
noi. Aceste ecuatii suplimentare noi trebuie sa fie ecuatii fizice care sa
tinacont de proprietatiile materialului dein care este facut corpul, de modul
de comportare al acestuia sub actiunea sarcinilor; astfel spus aceste ecuatii
fizice trebuie sa lege intre ele tensiunile cu deformatiile din intermediul
unor constante de material.
1.4. ECUATIILE DE CONTINUITATE A DEFORMATIILOR
(SAINT-V NANT)
1. Daca rezumam rezultatele
obtinute, vedem ca deplasarile unui punct dintr-un corp continu, elastic, sunt
definite prin trei functii de punct u,v,w iar pectiv cu ajutorul altor sase
functii:
.Este
insa esential sa remarcam ca aceste noua functii nu sunt independente astfel
de exemplu daca ne sunt date cele trei functii u,v,w atunci pe baza relatiilor
(1.3.12) pute determina toate celelelte sase componente ale deformatiilor ca
derivate de ordinul I ale functiilor u,v,w. Anseamna ca cele sase functii ale
componentelor deformatiei nu pot fi luate ocum (nu pot fi arbitrare): intre ele
trebuie sa existe anumite relatii pe care ne propunem sa le stabilim. Aceste
relatii sunt in numar de sase, si se impart in doua grupe: in prima grupa intra
relatiile care leaga componentele deformatiei din acelasi plan, iar in a doua
grupa relatii dintre componentele deformatiei din plane diferite.
2. Sa trecem la stabilirea relatilor din prima grupa. Idea de baza consta in a eliminadeplasarile intre expresiile componentelor deformatiilor din acelasi plan, pornind de la relatiile (1.3.12). Astfel diferentiem primele doua ecuatii;
(+)
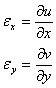
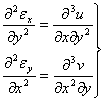Prin adunare si tinind cont de expresia lui 
obtinem:
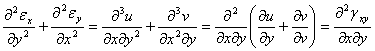
Prin urmare, pentru fiecare punct exista o relatie intre lungirile specfice si unghiul de lunecare din fiecare plan, de forma:
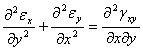(1.4.1)
Asta inseamna ca daca sunt date expresiile a doua deformatii liniare, cu ajutorul acestora putem determinasi unghiul de lunecare, care nu poate avea o marime arbitrara, ci este:
(1.4.2)
3. Sa trecem la stabilirea relatilor din cea de-a doua grupa, urmarind un rationament analog de eliminare a deplasarilor intre relatiile (1.3.12) prin derivare:
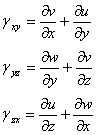
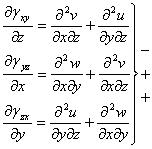
Din suma ultimelor doua relatii o scadem pe prima si obtinem:
Aceasta relatie o mai diferentiem odata in raport cu z si obtinem:
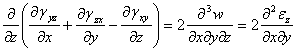(1.4.3)
Aceasta este una din relatiile
grupei a doua; rezulta de aici ca daca ne sunt date trei deformatii unghiulare
specifice (
),
cu ajutorul lor putem determina complet alungirea specifica 
,
care deci nu poate fi aleasa in mod arbitrar, ci va fi:
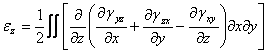(1.4.4)
Obtinemin final, prin permutari circulare, urmatorul sistem de ecuatii:
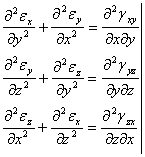
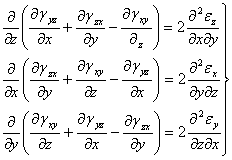
Aceste ecuatii se numesc " ecuatii de compatibilitate sau de continuitate a deformatiilor " ele au fost deduse de Saint-Venent.
4. Sensul fizic la acestor relatii
este urmatorul. Sa ne imaginam ca, corpul elastic supus deformatiei l-am
sectionat in paralelipipede infinit mici. Sa dam fiecarui paralelipiped
elementar o deformatie arbitrara, determinata de cele sase marimi () dar
astfel incat componentele deformatiei pentru diferitele
paralelipipede constitutive sa nu fie legate intre ele. Sa incercam
acum sa reansamblam corpul cu ajutorul paralelipipedelor elementare deformate.
Vom constata ca-
in cazul general aceasta operatie se dovedeste a fi imposibila: intre anumite elemente
apar spatii goale, pentru alte elemente nu este loc suficient, astfel incat din
elementele deformate nu mai putem sa reconstituim un corp elastic continuu.
Insa noi stim ca deformatia reala a corpului se face astfel incat el ramane si
dupa deformatie un mediu continuu, adica in interiorul lui nu apar
discontinuitati(fisuri, ruperi, goluri). Concluzia care rezulta de aici este ca
de fapt, componentele deformatiilor trebuie sa satisfaca anumite relatii.
Acestea sunt relatiile(1.4.5) care pe baza consideratiilor de mai sus, capata
un sens nou, fizic, si isi justifica denumirea de relatii de continuitate a
deformatiilor. Ele ne asigura ca, corpul dat, continuu inainte de deformatie,
ramane continuu si dupa deformatie.
5. In mod practic se pot ivi doua situatii distincte:
a.) Sa presupunem ca sarcinile sunt date; daca vom reusi sa determinam direct deplasarile punctelor din corp u, v, w, atunci deformatiile vor putea fi calculate cu formulele(1.3.12). In acest caz conditiile de compatibilitate(1.4.5) sunt satisfacute in mod automat deoarece ele sunt deduse din ecuatiile(1.3.12) si sunt o consecinta a acestora.
b.) Daca din sarcinile date, vom reusi sa gasim mai intai tensiunile si dupa aceea deformatiile, va fi obligatoriu ca in acelasi timp sa satisfacem si ecuatiile de continuitate. In caz contrar deformatiile vor fi incompatibile intre ele si nu vom mai putea gasi deplasarile din ecuatiile(1.3.12), intrucat ele vor contine contradictii reciproce.
Aspectul fizic al problemei.
Legea lui Hooke generalizata
1.5.1. Criterii si ipoteze.
1. Am studiat pana acum teoria tensiunilor reprezentand aspectul static al problemei fundamentale a mecanicii mediului continuu; teoria deplasarilor si deformatiilor, reprezentand aspectul geometric al aceleasi probleme: determinarea tensiunilor si deformatiilor unui corp solid in orice punct al sau. Aceste doua teorii nu sunt insa suficiente pentru rezolvarea problemelor fizice cu privire la determinarea deformatiilor care se produc in corpul elastic sub actiunea sarcinilor, atata timp cat tensiunile si deformatiile specifice nu sunt legate intre ele printr-o lege oarecare. Natura fizica a acestei legi consta in faptul ca ea trebuie sa coreleze cele doua aspecte ale solidului si fiind legate de particularitatile microstructurii corpului, constituie de fapt obiectul de studiu al fizicii. Pentru a obtine insa doua forme convenabile din punct de vedere tehnic, subintelegem ca notiunile cu care operam, sunt de fapt valori medii statice.
2. Stabilim relatiei dintre tensiuni si deformatii in cazul starii spatiale de eforturi se va face prin extinderea legilor lui Hooke din cazul intinderii si alunecarii simple.
Posibilitatea practica de a face o astfel de extrapolare este justificata experimental pentru majoritatea materialelor tehnice, daca se respecta urmatoarele conditii:
prezenta simultana a tuturor componentelor tensiunilor, ca si actiunea lor separata(daca este posibila) nu aduce materialul in stare plastica;
practic materialul poate fi considerat omogen si izotrop;
- deformatiile sunt infinit mici in comparatie cu dimensiunile corpului studiat;
- procesul de deformatie este izoterm.
Aceste ipoteze asigura in mod practic posibilitatea aplicarii principiului independentei actiunii fortelor si utilizarea legilor elementare unidimensionale, la determinarea deformatiilor dupa orice directii in interiorul oricarui paralelipiped elementar.
3. Intr-o alta forma aceste consideratii constituie de fapt datele unei "leme", conform careia: " intr-un corp elastic omogen si izotrop, tensiunile normale nu pot provoca lunecari si invers, tensiunile tangentiale nu dau nastere la lungiri". Numai astfel se poate intelege posibilitatea aplicarii suprapunerii de efecte la stabilirea legii lui Hooke pentru starea spatiala de solicitare.
1.5.2. Stabilirea legii lui Hooke generalizata
Vom incepe studiul nostru considerand un
paralelipiped cu muchiile egale cu unitatea pe care actioneaza numai tensiunea
normala ;
se vor produce: o lungire specifica in directia axei x, data de legea lui
Hooke:
si niste scurtari(contractii transversale) dupa directia axelor y si z,
perpendiculare pe axa x:
unde
E- este modulul de elasticitate longitudinal constant pentru un material
izotrop in domeniul elastic iar -
coeficientul lui Poissonx). Se produc situatii analoage daca
actioneaza numai tensiunea 
sau
;
rezultatele le-am centraliza in schema urmatoare:
 |  | |
Tensiunea care Deformatia Deformatia Deformatia
actioneaza dupa axa x dupa axa y dupa axa z
 |
 |
|
x) In cazul deformatiilor finite acest coeficient nu va fi constant, ci chiar pentru un proces elastic va deveni o functie de valoarea deformatiei propriu zise; in domeniul micilor deformatii, specifice teoriei liniare a elasticitatii el poate fi considerat constant.
Insumand efectele vom obtine alungirile specifice dupa cele trei axe:
(1.5.1)
Lasand sa actioneze numai tensiunile tangentiale, de
exemplu 
,
acestea produc o deformatie a fetelor paralele cu planul xOy, fara a influenta
celelalte fete ale paralelipipedului. Atunci, conform legii lui Hooke pentru
forfecare(sau lunecare) simpla, avem:
In final, sub actiunea tuturor tensiunilor tangentiale componentele lunecarilor specifice vor fi
(1.5.2)
Ansamblul celor doua grupe de relatii (1.5.1) si (1.5.2) reprezinta asa numita lege generalizata a lui Hooke pentru un corp solid, elastic, omogen si izotrop; ea se mai numeste si legea elasticitatii corpului izotrop si poate fi formulata astfel: "intre componentele tensorului deformatie intr-un punct dat al unui corp elastic omogen si izotrop si componentele tensorului tensiune, corespunzator aceluiasi punct, exista o relatie de dependenta liniara".
Metodele fundamentale de rezolvare a
problemei teoriei elasticitatii
1.6. Privire de sinteza.
1. Odata cu stabilirea legii generalizate a lui Hooke, am incheiat si deducerea tuturor grupurilor de ecuatii fundamentale din elastostatica liniara a solidului deformabil omogen si izotrop. Acestea sunt:
Ecuatii statice: Ecuatiile diferentiale de echilibru ale lui Navier-Cauchy.(1.1.6)
Ecuatii geometrice: Ecuatiile lui Cauchy, care leaga deformatiile cu deplasarile.(1.3.12)
Ecuatii fizice: Legea lui Hooke generalizata(1.5.1) si (1.5.2)
La aceste grupuri fundamentale de ecuatii se mai adauga:
-conditiile la limita(care in cazul static sunt conditii pe contur) (1.2.6)
-ecuatiile de compatiblitateale lui Saint-Venant(1.4.5)
2. Avem de-a face cu un sistem de 15 ecuatii cu 5 necunoscute; aceste necunoscute sunt:
- sase componente ale tensiunilor 
- sase componente ale deformatiei
- trei componente ale deplasarii u, v, w.
Astfel din punct de vedere matematic problema poate fi rezolvata si se reduce la gasirea a 15 functii care sa satisfaca cele15 ecuatii fundamentale cu conditii la limita date si cu verificarea ecuatiilor de continuitate.
Dezvoltarea teoriei elasticitatii a aratat ca rezolvarea problemei se poate face prin procedee diferite; s-au fundamentat insa doua metode indirecte:
a) Dupa prima metoda se aleg ca necunoscute fundamentale ale problemei - deplasarile punctelor corpului elastic; aceasta inseamna ca in fiecare punct al corpului vom avea trei functii de punct necunoscute:
(1.6.11)
care trebuie sa satisfaca cele trei ecuatii de echilibru(1.1.6) si conditiile pe suprafata (1.2.6) care contin fortele exterioare (sarcinile):qnx,qnz,qnz.
Pentru obtinerea ecuatiilor (1.6.1) este necesar sa se inlocuiasca relatiile geometrice (1.3.12) in ecuatiile fizice, adica este necesar ca tensiunile sa fie exprimate in functie deplasari si sa fie introduse in cele trei ecuatii de echilibru(1.1.6). Prin urmare, natura ecuatiilor (1.6.1) ca si a grupului(1.1.6) este statica. Vom numi aceasta metoda: "metoda deplasarilor".
b) Dupa cea de-a doua metoda se aleg metode fundamentale-tensiunile; atunci in fiecare punct al corpului von avea sase functii necunoscute:
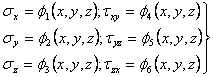(1.6.2)
Problema se reduce la determinarea acestor sase functii care trebuie sa satisfaca cele trei ecuatii de echilibru (1.1.6); aceste ecuatii nu sunt insa suficiente ca numar si va trebui sa le atasam inca sase ecuatii de continuitate (1.4.5). in acela timp trebuie sa ,fie satisfacute si conditiile la limita (1.2.6).
Evident ca se poate imagina si o metoda mixta cind se iau ca necunoscute principale anumite deplasari si anumite tensiuni. Problemele teoriei elasticitatii se pot rezolva mai usor alegand ca necunoscute numai tensiunile sau numai deplasarile, dupa cum se pun conditiile la limita, si eliminand celelalte necunoscote intre cele 15 ecuatii specificate mai sus. In felul acesta suntem condusi la o rezolvare in tensiuni sau la o rezolvare in deplasari a acestor probleme.
1.7. ECUATIILE LUI LAME. REZOLVAREA PROBLEMEI
TEORIEI ELASTICITATII IN DEPLASARI.
Incepem cu aceasta metoda, care deobicei este
numita:"a doua problema fundamentala a teoriei elesticitatii", deoarece este
mai simpla din punct de vedere matematic, avand mai putine necunoscute,
utilizind deci un numar mai mic de ecuatii. In acest caz conditiile pe contur
se pun sub forma:
(1.7.1)
unde
deplasarea 
a punctelor denormala exterioara n este data
de legatura cu celalalte corpuri.
Sunt rare cazurile in care se pot pune conditii in deplasari pe tot conturul; eventual se pun conditii pentru anumite derivate ale deplasarilor - de exemplu pentru deformatii specifice. Trebuie mentionat ca aceste conditii sunt diferite de coditiile defixitate sau conditiile de rezemare ale corpului, care se pun in puncte pentru determinarea miscarii de corp rigid a acestuia.
Cautam sa exprimam toate necunoscutele, in functie de deplasari. Pornim, inlocuind in ecuatiile fizice, relatiile geometrice, -pentru tensiuniile decare avem nevoie in prima ecuatie de echilibru static (1.1.6):
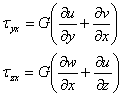(1.7.2)
Derivam aceste ecuatii si obtinem:
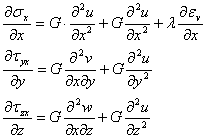(1.7.3)
Introducem aceste relatii in prima ecuateie de echilibru (1.1.6):
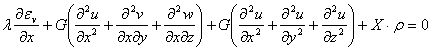(1.7.4)
Expresia din prima paranteza se poate scrie mai scurt, astfel:
Pemtru o scriere mai prescurtata se
introduce si operatorul diferential al lui Laplace (notat cu 
-
numit"laplasian" ; uneori mai este notat cu 
-
citit "nabla doi",sugerand legatura dintre cei doi operatori).
Cu aceste observatii, ecuatia (1.1.4) se scrie:
In mod analog se pot transforma si celelalte doua ecuatii din (1.7.6); ele se pot scrie si direct facand permutari circulare in (1.7.7) ale literelor (x,y,z) si (u,v,w). Se ajunge astfel la urmatorul system de ecuatii fundamentale ale teoriei elasticitatii exprimate in functie de deplasari:
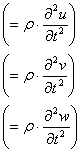(1.7.8)
Ecuatiile (1.7.8) se numesc ecuatiile lui Lame. Ele reprezinta o sinteza a studiului efeectuat pana acum asupra tensiunilor, deformatiilor si relatiilor dintre tensiuni si deformatii. Prin urmare ecuatiile lui Lame cuprind toate ipotezelede natura mecanica, geometrca si fizica pe care se bazeaza teoria elasticitatii. In adevar, aceste ecuatii :
Ø Exprima echilibrul static al fiecarei portiuni infinit mici din corp (daca partea din dreapta este egala cu zero) sau sunt ecuatii de miscare ale elementului (daca partea din dreapta este diferita de zero);
Ø Cuprind caracteristici geometrice ale deplasarilor si
deformatiilor (
);
Ø Cuprind factori fizici (
)
exrimand proprietatile elastice si densitatea corpului.
In mod similar se transforma si conditiile de suprafata (1.2.6)inlocuind tensiuniile in functie de deplasari:
Relatia poate fi scrisa mai simplu daca
luam in consideratie faptul ca expresiile din prima paranteza dreapta
reprezinta derivata functiei u(x,y,z) dupa normala n la suprafata cirpului:
Cu acest rationament vom obtine forma definitiva a conditiilor de suprafata:
Ecuatiile lui Lame (1.1.8)impreuna
cu comditiile pe suprafata (1.1.10), ne permit sa trecem direct la rezolvarea
problemelor de elasticitate (1.1.8) si sa gasim functiile (u,v,w) care satisfac
conditiile pe suprafata (1.1.10), atunci introducandu-le in (1.3.12) vom gasii
deformatiile specifice 
cu
ajutorul acestor deformatii, din legea luiHooke generalizata (1.5.1) si 1.5.2)vom
putea calcula tensiuniile 
.
ECUATIILE LUI BELTRAMI-MITCHEL.
REZOLVAREA PROBLEMEI TEORIEI ELASTICITATII
IN TENSIUNI
In
aplicatiile practice de cele mai multe ori cunoastem sarcinile exterioare ce
actioneaza pe contur; in fiecare punct de pe contur va trebui sa existe un
echilibru mecanic intre tensiunile interioare si sarcinile exterioare (de
componente 
;
le-am mai notat, pentru preciza ca este vorba de elemente de arie de la
suprafata corpului cu 
fiind
normala exterioara.Va trebui deci sa punem conditia ca pe contur tensiuniile
obtinute dincalcul sa fie egale cu sarcinile exterioare date folosind relatiile (1.2.6) sau relatii de tipul
(1.3.1) care se refera la directiile principale. Daca reusim sa integram
sistemul de ecuatiiconsiderat mai sus, indeplinind si conditiile pe contur, am
determinat in intregime starea de solicitare a corpului, problema elasticitatii
fiind complet rezolvata. Problea de mai sus in care se pun conditii in tensiuni
pe contur se numeste " prima problema fundamentala a teoriei elasticitatii".
Sa
presupunem deci ca ne alegem canecunoscute fundamentale cele sase tensiuni; 
.In acest caz cele trei ecuatii de echilibru
(1.1.6)nu sunt suficiente pentru rezolvarea problemei; le vom atasa si
ecuatiile de continuitate(1.4.5). Problema se reduce astfel la integrarea a
noua ecuatii cu sase functii necunoscute. Functiile arbitrare care rezulta prin
integrare se vor determina din conditiile la limita (1.2.6). deoarece
conditiile de compatibilitate (1.4.5) leaga intre ele deformatiile 
levom transforma exprimamdu-le in functie de
tensiuni cu ajutorul legii lui Hooke. Efectuand aceasta operatie si folosind
ecuatiile de echilibru (1.1.6) considerind ca fortele masice lipsesc sau sunt
constante, ecuatiile de continuitate (1.4.5) devin :
(1.8.1)
Acestea se numesc ecuatiile lui Beltramii-Mitchell. Asa dar, pentru rezolvarea problemei elasticitatii va trebui st integram noua ecuatii (1.1.6) si (1.14.1), iar dupa acea sa satisfacem conditiile pe suprafata (1.2.6).
Concluzii: La rezolvarea problemelor teoriei elasticitatii in functie de tensiuni sau de deplasari, se poate pune intrebarea daca solutia obtinuta este univoca sau nu; sa le corespunda in interiorul corpului citeva sisteme de tensiuni in loc de unul singur sau altfel spus deplasarilor sau tensiunilor date in interiorul corpului corpului nu le-ar putea corespunde diferite conditii pe contur. Aceasta de fapt este problema de unicitate a solutiei a carei demonstratie se poate gasi in cartile de specialitate.Subliniem insa ca unicitatea este asigurata numai in teoria liniara a elasticitatii.
1.9. Introducerea functiei de tensiune AIRY
Metoda obisnuita de rezolvare a sistemului de ecuatii cu derivate partiale (1.1.6)
consta in introducerea unei functii de tensiune sau funtii potential. In probleme de elasticitate
plana, ea a fost folosita pentru prima data de catre Airy (1862) si-i poarta numele.
Se considera mai intai in relatiile (1.1.6) ca fortele masice sunt nule.
Se observa ca daca tensiunile 
si 
se exprima prin intermediul unei functii 
sub forma:
, (1.9.1)
prima ecuatie (1.1.6) este identic verificata. In mod asemanator,
cea de a doua ecuatie este verificata identic daca si 
se exprima printr-o functie 
:
, 
. (1.9.2)
Deoarece 
,
rezulta ca cele doua functii si nu sunt independente, intre ele existand
relatia:
(1.9.3)
Aceasta conditie este satisfacuta,
daca functiile si sunt derivate ale unei alte functii 
,
adica:
si 
. (1.9.4)
Inlocuind
relatia (1.9.3)in (1.9.1)si (1.9.2)rezulta ca ,
si se exprima in functie de prin relatiile:
, 
. (1.9.5)
Ducand relatia (1.9.5)in cea de a treia ecuatie (1.1.6) se deduce ca functia trebuie sa satisfaca ecuatia:
,
care se mai poate scrie simbolic:
,
sau dezvoltat:
. (1.9.6)
Functia
care satisface ecuatia este numita functie biarmonica iar 
se numeste operator biarmonic.
Daca
sistemul (1.1.6) este neomogen (
si 
nu sunt nule), primele doua ecuatii sunt
satisfacute identic de expresiile:
(1.9.7)
care inlocuite in a treia ecuatie conduc la ecuatia pentru :
. (1.9.10)
Se observa
ca pentru fortele masice si constante
sau nule, singurele cazuri de interes practic, ecuatia (1.9.10) se transforma
in (1.9.6), adica functia potential este o functie biarmonica.
1.10.Interpretarea mecanica a functiei de
tensiune pe contur
Se
considera o saiba delimitata de un contur simplu conex, actionata doar de
fortele de contur
,
.
Functiei de tensiune si derivatelor sale li se pot da pe contur semnificatii
mecanice deosebit de utile in aplicatiile practice. Fie conturul din figura
1.10.1, a pe care se alege o origine arbitrara 
pentru masurarea arcelor.
|
|
Fig.1.10.1
Parcurgand conturul
in sens trigonometric, astfel incat domeniul saibei sa ramana la stanga, se va
putea scrie pentru cosinusurile directoare ale normalei 
la contur:
(1.10.1)
unde s-a considerat (
)
in sensul cresterii lui
s. Tinand seama de relatiile
(1.10.1) si (1.9.5) conditiile de
contur se scriu astfel :
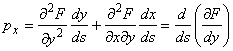
Integrand aceste relatii pe arcul s
pornind din ,
se obtin:
;
;
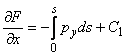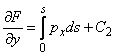unde 
si
sunt constante de integrare. Deoarece o
constanta intr-o derivata a functiei nu induce termini in expresiile
tensiunilor, acestea fiind date de derivate de ordinul doi ale functiei
(relatiile (1.9.5)), se poate considera 
astfel ca:
; 
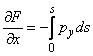, (1.10.2)
adica derivatele functiei de
tensiune in punctul curent 
sunt egale cu rezultantele incarcarilor de
contur de pe arcul 
.
Integrand prin parti diferentiala
totala a functiei :
pe contur se obtine:
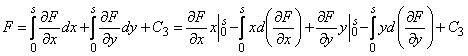
Considerand,
pe baza celor apreciate anterior, 
si tinand seama de relatiile (1.01.2), relatia
care da functia devine:
La
impunerea limitelor, s-a tinut seama ca, in baza relatiei (1.10.2):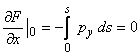 
si analog, 
.
Ordonatele 
fiind constante in raport cu variabila de integrare, relatia
pentru se mai poate scrie:
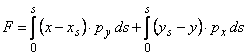(1.10.3)
care ne arata ca functia de tensiune in 
este numeric egala cu momentul fortelor de
contur ce actioneaza pe arcul ,
in raport cu punctul (fig.
1.10.2).
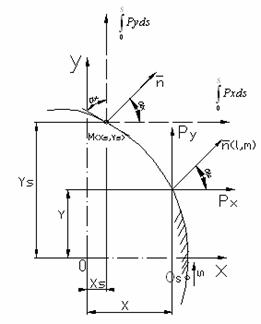
Fig.1.10.2
Pentru a preciza derivata functiei dupa normala la contur, din figura 1.10.1, b
se observa ca: 
; 
si deci, tinand seama si de relatia (22.16), rezulta:
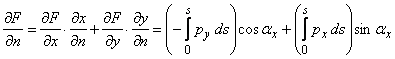(1.10.4)
Pentru
interpretarea rezultatului, se considera o bara fictiva care urmareste conturul
saibei, are o taietura in si este incarcata cu fortele distribuite si (fig. 1.10.2). Se observa ca prima paranteza
din membrul drept al ultimei egalitati (1.10.4) reprezinta rezultanta fortelor de pe ,
iar a doua paranteza, rezultanta fortelor . Produsul acestora cu 
,
respectiv 
da proiectia dupa tangenta in la contur. Rezulta ca derivata dupa normala
a functiei este egala cu forta axiala 
in bara fictiva.
Se verifica usor ca in interpretarea data relatiilor (1.10.3) si (1.10.4) sunt respectate si conditiile de semne din statica.
CAZURI PARTICULARE ALE STARII TRIAXIALE DE SOLICITARE, PROBLEMA PLANA IN COORDONATE CARTEZIENE
1.11. STAREA DE TENSIUNE PLANA. ECUATIILE LUI LEVY.
Vom studia o categorie de probleme, de mare aplicabilitate practica, numite "probleme plane" care sunt inportante simplificari de ordin matematic. La asemenea probleme, fie tensiunile, fie deformatiile, dupa una din axele de coordonate (de exemplu dupa axa oz) sunt nule si fenomenul se poate studia intr-un singur plan (de exemplu axa xoy). Din punct de vedere matematic o asemenea stare de solicitare se realizeaza foarte greu; din punct de vedere practicexista insa multe situatii care cu un anumit grad de aproximatie pot fi reduse la o asemenea stare plana, rezolvarea lor fiind mult mai usurata. In functie de marimile care sunnt nule sau se neglijeaza starile plane se inpart in doua mari categorii:
a. Stari
plane de tensiune, care apar in situatiile in care una din tensiunile normale
este nula(
);sa
notam de pe acum ca starea de deformatie a corpului este insa triaxiala;
b. Stari plane de deformatie, care apar an situatia in care una din componentele deplasarii este nula (w=0); in acest caz starea de tensiune este triaxiala.
Vom dezvolta in continuare metodele de studiu pentru fiecare caz in parte.
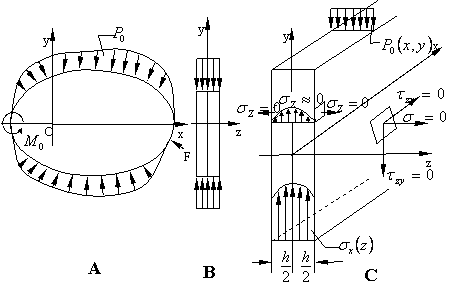O
stare de tensiune plana apare-de exemplu-in cazul unei placi subtiri (grinda,
bara) supusa la actiunea unor forte aplicate pe conturul ei, paralele cu planul
acesteia si uniform distribuite pe grosimea ei (fig 1.11.1). Desi grosimea
placii in directia axei oz este mica, atata timp cat sarcina nu depaseste o
anumita limita placa nu se va incovoia in drectia axei oz(nu ne preocupam de
problema voalarii placii).
Asemenea elemente de rezistenta cu asemenea caracteristici sunt denumite de obicei grinzi perete (dupa literatura elvetiana si rusa), saibe(dupa literatura germana) sau discuri (dupa literatura fraceza si engleza) desi uneori aceste denumiri au si alte semnificatii. Exemplele practice sunt numeroase: grizi pereti pentru silozuri, buncare etc. , consolele scurte pentru poduri rulante, colturile de cadru, carlige, biele, elemente de constructii si rigidizare pentru vase, aripi de avion etc..
Deoarece-conform datelor problemei- fetele placii (paralele planului
xoy) sunt libere de sarcini, componentele tensiunilor 
, sunt
egalecu zero pe ambele fete laterale; mai mult datorita grosimii mici a
corpului putem presupune,-fara a face o eroare prea marw- ca si in interiorul
placiiaceste tensiuni sunt nule (ele vor fi n orice cazfoarte mici). Rezulta ca
vom avea peste tot:
(1.11.1)
deci starea de tensiune este zero.
Pentru acelasi motiv- grosimea mica a placii- este firesc sa presupunem
ca celelalte trei componente ale tensiunilor 
, nu
depind de coordonata z, adica vor varia foarte putin de-a lungul axei oz (sunt
constante pe intreaga grosime a placii. Vom lucra de fapt cu valori medii.).
Asa dar, in problema data tensiunile satisfac urmatoarele conditii:
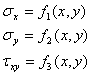
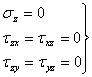(1.11.2)
Sa analizam putin care ar fi starea de deformatie a corpului in acest caz. In general deformatiile si deplasarile care se produc pe directia coordonatei z nu prezinta interes practic; ele se pot totusi determina usor daca se cunosc componentele tensiunilor si deformatiilr paralele cu planul xoy al placii. Astfel :
si 
(1.11.3)
care
rezulta din legea lui Hooke 
inlocuind 
si 
; 
.
Sa vedem ce devin cele 15 ecuatii fundamentale ale
teoriei elasticitatii in cazul analizat al starii plane de tensiune vom
considera situatia cea mai frecventa, cand fortele de volum sunt reprezentate
numai de greutatea proprie, deci: 
(q- greutatea unitatii de volum)(am schimbat putin sistemul de axe considerind in planul vertical xoy).
Se obtine deci:
I. Ecuatiile diferentiale de echilibru
(1.11.4)
II. Conditiile pe contur
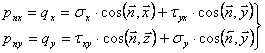(1.11.5)
III. Ecuatiile geometrice
(1.11.6)
IV. Ecuatiile fizice
(1.11.7)
V. Conditiile de compatibilitate
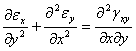(1.11.8)
Se
oobtine deci, in final, un sistem de opt ecuati diferentiale cu opt neconoscute
care poate fi rezolvat fie prin metoda
fortelor, fie prin metoda deplasarilor sau eventual printro metoda mixta.
Sa ilustram acest caz, alegand ca necunoscute fundamentale, tensiunile, dupa modelul de rezolvare propus de M. levy. Vom porni de la ecuatia de continuitate care trebuie transformata introducand in locul deformatiilor expresiile lor in tensiuni exprimate prin legile fizicii (1.11.7):
(1.11.9)
Daca la aceasta ecuatie se mai adauga ecuatiile de echilibru static obtinem un sistem de trei ecuatii cu trei necunoscute, in tensiuni. Insa relatia (1.11.9) poate fi adusa la o forma mai simpla daca derivam ecuatiile de echilibru si le adunam:
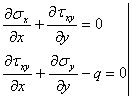
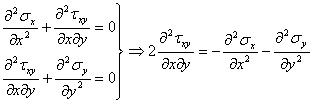
Inlocuind acest rezultat in ecuatia de compatibilitate (1.11.9) se obtine o forma numai in tensiuni normale numita "ecuatia lui Levy" sau "conditia lui Levy":
sau introducand operatorul armonic al lui Laplace :
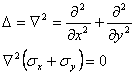(1.11.11)
Asa dar, in cazul starii plane de tensiune, cand fortele de volum sunt reprezentate numai de greutatea proprie, grupul de ecuatii fundamentale al teoriei elasticitatii se reduce la urmatoarele trei:
(1.11.12)
In legatura cu acest rezultat facem acum o observatie deosebit de importanta (facuta pentru prima oara de M.Levy), cu o covarsitoare aplicabilitate practica. Daca intr-o problema ne intereseaza numai starea de tensiune, atunci putem sa ne rezumam la ecuatiile (1.11.12) n care nu intra constantele elastice de material. Asa dar, starea de tensiune intr-o problema plana nu depinde de natura materialului (uneori acest rezultat este cunoscut in literatura sub numele de "Teorema lui Levy". Aceasta concluzie sta la baza aplicariii metodelor optice de studiere a starilor de tensiune cu ajutorul luminii polarizate (fotoelasticimetrie );in aceste cercetari experimentale materialul dat este inlocuit printr-un alt material, transparent, optic activ (cu proprietati de birefrigentaaccidentala) din care se confectioneaza un model al piesei reale. Rezultatele obtinute pe model pot fi astfel transpuse la piesa dintr-un alt material fara a ne pune problema de similitudine; baza teoretica este data de ecuatiile in tensiuni (1.11.12).
1.12. STAREA DE DEFORMATIE PLANA
Sa consideram un corp solid deformabil aflat intr-o stare oarecare de eforturi; daca deplasarile tuturor punctelor acestuia se pot produce numai dupa doua directii, adica numai intr-un singur plan, sau altfel spus, daca una din componentele deplasarii (de exemplu w) este egala cu zero iar celalalte doua u si v nu depind de coordonata z corespunzatoare deplasarii w, zicem ca avem cea ce se numeste o stare de deformatie plana. Un exemplu care ilustreaza bine o asemenea stare de solicitare, este dat de un corp deformabil, fixat intre doua placi perfect rigide (fig. 1.10.1) situate la distanta constanta si care este comprimat de forte paralele planele placilor.
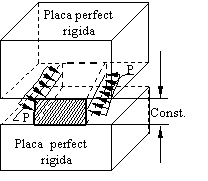Rezulta
de aici ca o asemenea stare de solicitare este caracterizata, pentru toate
puncteele corpului de deplasarile:
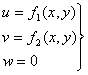(1.12.1)
si deformatiile specifice:
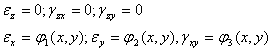(1.12.2)
Aceste
ecuatii ne arata ca toate deplasarile si deformatiile au loc exclusiv in
directia planului xoy, in toate sectiunile corpului paralele planului xoy
(oricare ar fi z=
=constant)
deplasarile si deformatiile sunt aceleasi. De aceia deformatiile de acest gen
se numesc deformatii plane.
In
tehnica se intalnesc si alte cazuri de corpuri care pot fi considerate ca se
afla intr-o stare plana de deformatie, cum sunt de exemplu:barajele (fig1.12.2.a),
rulourile(b), boltile cilindrice (c), placile lungi (d) etc. Asemenea probleme
pot fi asimilate sau modelate cu cazul unui corp prismatic sau cilindric cu una
din axe paralela cu axa oz, incarcat pe suprafata laterala cu o sarcina normala
pe directia oz si uniform repartizata dupa aceasta directie. Sa justificam
afirmatia ca acest corp (model) se afla intr-o stare de deformatie plana: vom
izola din corp, la o distanta suficient de mare de extremitati, un element
subtire impreuna cu sarcina respectiva.
Sa presupunem ca acest element
lucreaza ca un corp elastic independent; atunci in el ar trebui sa apara
deformatii bupa directia axei oz. In realitate, datorita existentei elementelor
vecine si interactiunii dintre ele, nu vor aparea nici deformatii nici
deplasari de-a lungul axei oz, dar ca urmare a impiedicarii deformatiilor deci
ca o consecinta a disparitiei componentei , vor apare tensiuni normale . Rezulta ca starea de tensiune este de fapt
spatiala Intradevar, din cea dea treia ecuatie a lui Hooke:
(1.12.3)
Deci, 
si
depinde de tensiunile fundamentale si
produse de sarcinile exterioare.
In aceste conditii grupul ecuatiilor
fundamentale se simlifica foarte mult. Ecuatiile de echilibru, ecuatiile
geometrice si conditiilela limita raman in forma anterioara data de starea
plana de tensiune in ipoteza ca fortele de volum sunt reprezentate numai de
greutatea proprie. Se modifica numai ecuatiile fizice,care pentru dat de relatia (1.12.3)obtin forme noi:
(1.12.4)
Daca se repeta operatii analoge cu cele expuse anterior, ecuatia de continuitate devine:
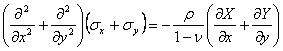(1.12.5)
care pentru fortele de volum constante se transforma de asemenea in conditia lui Levy:
(1.12.6)
in baza acestor constatari se poate deci afirma ca tensiunile care caracterizeaza starea plana de deformatie sunt:
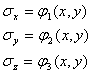
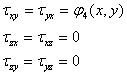
adica toate tensiunile care sunt diferite de zero nu depind de coordonata z, cea ce desigur putea fi afirmat si a priori.
PROBLEMA PLANA IN COORDONATE POLARE
1.13. ECUATIILE GENERALE ALE PROBLEMEI ELASTICE
PLANE EXPRIMATE IN COORDONATE POLARE
1.Exista numeroase cazuri de corpuri care prezinta o simetrie axiala, ca de exemplu: tuburile cu pereti grosi, inelele circulare, discurile in miscare de rotatie etc, la care determinarea tensiunilor si deformatiilor din solicitarile exterioare se face mult mai simplu daca se utilizeaza coordonatele polare.
Sa
consideram un astfel de corp cu axa longitudinala dirjata in lungul axei z si
sarcina exterioara paralela planului xOy- prin datele problemei-. In acest caz,
asa cum am vazut atit pentru starea de tensiune plana cit si pentru deformatia
plana, putem sa nu tinem seama de axa Oz si prin urmare intrega problema se va rezolva intr-un singur plan
folosiind coordonatele polare r si 
.
Ne propunem sa regasim toate ecuatiile fundamentale ele problemei plane a teoriei elasticitatii exprimate in coordonate polare si ulterior se exemplifica aplicarea acestor ecuatii pentru cateva tipuri de corpuri cu larga aplicabilitate tehnica.
2.Sa ne fixam notatiile. Pentru aceasta in locul paralelipipedului
elementar cu fete dreptunghiulare, utilizat pana acum, vom izola din corp un
element de volm cu grosime egala cu unitatea (dimensiunea in lungul axei z
egala cu un milimetru) si cu celalalte patru fete obtinute in modul urmator: cu
ajutorul a doua plane radiale perpendiculare pe placa (pe corp), care fac intre
ele unghiul infinit mic dQ si cu ajutorul a doua suprafete cilindrice
concentrice de raze r si (r+dr) (fig 1.13.1)- infinit apropiate-. Laturile
acestui element de volum in planul xy vor fi: 
Sa
consideram u system de referintacu centrul in 
si axele 
(orientata
radial) si 
-
perpendiculara pe aceasta- orientata deci dupa tangenta la cercul de raza 
;
folosindu-ne de aceste axe sa notam tensiunile care lucreaza pe fetele
elementului de volum, conform unor reguli cunoscute (v.fig.1.13.1).
Componentele tensiunii normale vor fi: 
-tensiunea
normala in sens radial sau componenta orientata dupa raza; 
-tensiunea
normala tangenta sau componenta orientata dupa tangenta la cercul de raza 
La variatia coordonatelor cu marimi infinit mici (dr sau dQ )
tensiunile, care sunt functii continue de punct vor varia de asemenea cu
cantitati infinit mici 
Se
procedeaza in mod asemanator si cu tensiunile tangentiale 
.
ECUATIILE DIFERENTIALE DE ECHILIBRU STATIC
3. Sa scriem conditiile de echilibru ale elementului abcd proiectind
fortele aplicate pe fetele sale dupa axele r si;
vom neglija fortele masice si deoarece grosimea elementului dupa axa oz este
egala cu unitatea, nu o vom mai evidentia distinct in ecuatiile de echilibru.
a.Suma proiectiilor fortelor dupa axa r:
(1.13.1)
b.Suma proiectiilor fortelor dupa axa Q
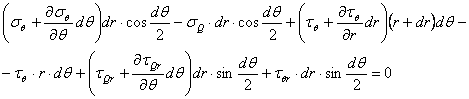
(1.13.2)
Deoarece unghiul dQ este mic,se poate scrie:
; se
desfac parantezele, se reduc termenii asemenea, se neglijeaza infinitii mici de
ordinul trei si se obtine:
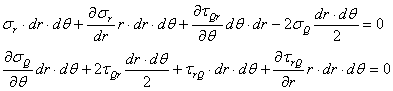
Daca se
inparte cu 
(de fapt cu 
) se
obtine in final ecuatiile diferentiale de echilibru ale elementului de volum exprimat
in coordonate polare:
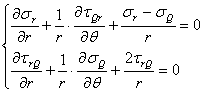(1.13.3)
c.Ecuatia de momente in raport cu centrul 
al
elementului se scrie sub forma:
S-a demonstrat astfel si aici principiul dualitatii tensiunilor tangentiale (acest rezultat l-am folosit deja la scrierea ecuatiilor 1.13.3)
RELATIILE DIFERENTIALE INTRE DEFORMATII SI DEPLASARI
4.Sa ne ocupam acum de relatiile dintre deformatii si deplasari.
Vom nota:
Ø Deplasarile punctelor de-a lungul axei r cu u
Ø Deplasarile punctelor de-a lungul axei Q cu v
Ø Lungirea specifica de-a lungul axei r (lungirea
specifica pe directia radiala-"lungirea specifica radiala"-) cu 
Ø Lungirea specifica de-a lungul axei Q ("lungirea
specifica circumferentiala") cu 
Ø Lunecarea specifica adica deformatia unghiului drept
BAD cu 
Sa urmarim procesul de deformatie al trapezului curbiliniu elementar ABCD, prezentat in detalium in figura (1.13.2), descompus in mod conventional in citeva etape componente:
Ø
El sufera, de exemplu, o deplasare in lungul axei r,
cu deformatia corespunzatoare a laturilor,trecind din pozitia ABCD in pozitia 
;
Ø
Are dupa acea o deplasare in lungul axei Q- cu
deformatia corespunzatoare laturilor-, trecind din poziotia in
pozitia 
;
Ø
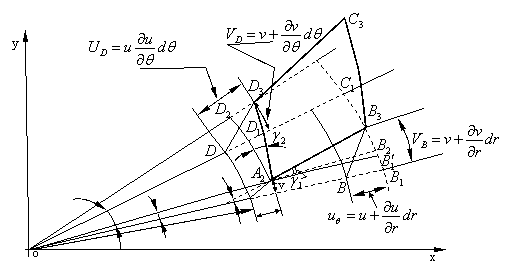
Considerand
si aparitia unor deformatii unghiulare sub actiunea tensiunilor tangentiale (
deci rotind laturile 
)
elementul trece din pozitia inpozitia 
.
Evident ca aceasta schema de deformare este numai un model, un mod de a ne reprezenta mcit mai intuitive procesul real complex de deformare a elementului de volum.
5.Sa stabilim componentele deplasarilor diferitelor puncte ale elementului.
Punctul 
sufera deplasariile 
=u
si 
Deplasarea punctului 
o vom gasii prin dezvoltarea in serie Taylor a
eunctiilor 
din care retinem numai termenii de ordinul
intii:
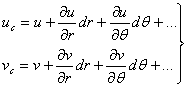(1.13.4)
Pentu celelalte puncte care au pozitii mai particulare se obtin urmatoarele componente pentru deplasari:
(1.13.5)
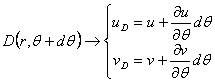(1.13.6)
(am
facut pe rind in 1.13.4, 
si dr=0).
6.Sa trecem acum la calculul deformatiilor specifice.
A.
Deformati specifica pe directia radiala este egala cu diferenta
dintre lungimea fimala si lungimea initiala a elementului 
raportata
la lungimea initiala:
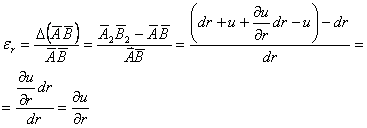(1.13.7)
B. Deformatia specifica in directia radiala 
Aceasta lungime specifica este mai greu de
calculat; eaa este o consecinta a doua cause:
In primul rind cind au loc numai deplasari radiale lugime specifica a
elementului 
(deci cresterea arcului AD datorita cresterii
razei cu u) va fi egala cu:
(x)
In al doilea rind, din cauza deplasarii v de-a lungul axei Q a
punctului A si a deplasarii 
a punctului D; lungimea arcului AD va fi egala
cu:
iar lungimea specifica:
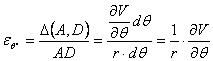(xx)
Atunci, lungirea specifica totala de-a lungul axei Q va fi:
(1.13.8)
C. Lunecarea specifica 
.
Ea reprezinta miscarea unghiului drept BAD datorita rotirii laturi 
in 
cu unghiul 
si al laturii 
(cu unghiul 
).
Sa calculam pentru inceput unghiul .
Urmarind figura 1.13.2 avem evident:
(ca unghi
exterior)
.
Unghiul 
rezulta imediat
Pentru
calculul lui 
,
ducem din punctual 
parplela 
Atunci:
Arcul 
Iar 
Deoarece:
Rezulta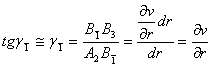 
Deci: 
(1.13.9)
Deformatia unghiulara datorata rotirii latirii 
va fi 
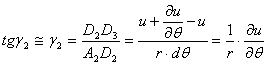(1.13.10)
lunecarea specifica are in final expresia:
(1.13.11)
In felul acesta, ecuatiile geometrice car leaga deformatiile specifice de deplasari, au in coordonate polare forma:
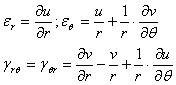(1.13.12)
ECUATIILE DE CONTINUITATE.
7.Am vazut cA grupul de ecuatii de continuitate, in cazul problemei
plane, se reduce la o singura ecuatie: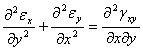
Pornind
de la aceasta ecuatie am gasit ecuatia lui
Levy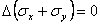 
si de aici folosind functia de tensiune al lui
Airy F(x,y) am aratat ca aceasta trebuie sa verifice ecuatia biarmonica:
sau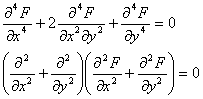 
(1.13.13)
Aceasta este forma ecuatiei de continuitate in coordonatee carteziene exprimata cu ajutorul functiei de tensiune F.
Sa transformam aceasta ecuatie in coordonate polare .Se vede ca pentru aceastatrebuie sa exprimam in coordonate polare atit functia de tensiune F(x,y) cit si derivatele sale successive, Pornim de la relatia de transformare a coordonatelor carteziene in coordonate polare:
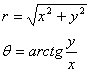(1.13.14)
Caut
expresiile lui 
;derivez
ultimul grup de relatii:
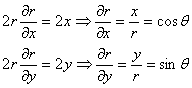(1.13.15)
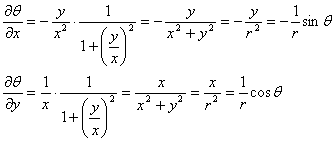
Trecem
acum la calculul derivatelor functiei de tensiune F(x,y) (sau 
):
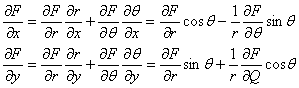
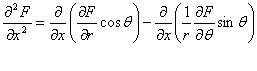
Dar:
(xx)
Daca scadem ultime le doua rezultate se obtine:
(x)-(xx)=
Intru totul asemanator se obtine:
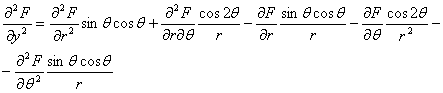
(1.13.16)
Folosind aceste relatii se gaseste cu usurinta ca:
(1.13.17)
Rezulta deci operatorul lui Laplace are in coordonate polare forma:
(1.13.18)
astfel
incat ecuatia de continuitate (1.13.13) exprimata prin functia de tensiune 
se poate scrie:
(1.13.19)
sau: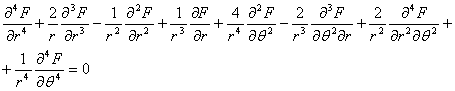
(1.13.20)
9.Cunoscand functia de tensiune obtinuta
prin rezolvarea acestei ecuatii, se pot obtine si expresiile tensiunilor 
date
in coordonate carteziene de relatiile (1.13.6):
Putem
calcula direct tensiunile in coordonate polare, observind ca daca dirijam axa x
ce-a lungul razei r, iar axa y de-a lungul axei atunci:
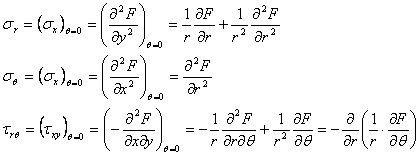
Deci si aici in cadrul elasticitatii
plane in coordonate plane se pune aceasi problema ca la coordonatele
carteziene; sa gasim o functie de tensiune , care
sa verifice ecuatia biarmonica (1.13.20); cu ajutorul acesteia putem calcula
imediat tensiuniile folosind ecuatiile (1.13.21).
Legea lui Hooke are aceasi forma ca in coordonatele carteziene, se schimba numai notatia tensiunilor si deformatiilor, corespunzator noilor axe:
(1.13.22)
1.14. CAZUL STARILOR DE TENSIUNE SIMETRICE IN
RAPORT CU POLUL
SOLUTIA IN TENSIUNI
1.Vom aplica ecuatiilor deduse mai sus la rezolvarea unor probleme mai
simple. Cea mai simpla problema in care isi dovedesc utilitatea coordonatele
polare, este cea a starii de tensiune simetrice in raport cu polul,
caracterizata prin faptul ca in toate punctele unui cerc de raza r, tensiunile
sunt constante, adica nu depind de unghiul ; ca urmare
si dervatele lor in raport cu sunt
nule.,
Functia de tensiune a lui Airy poate fi luata in acest caz independenta
de unghiul ; F
(r). Operatorul lui Laplace devine:
(1.14.1)
iar ecuatia biarmonica de continuitate:
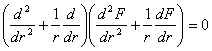(1.14.2)
pe care o vom scrie dezvoltat astfel:
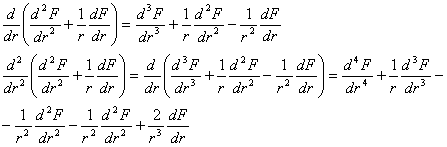
In final, ecuatia 1.14.2 devine:
(1.14.3)
In mod similar se simplifica si celelalte ecuatii ale starii plane:
I.Ecuatiile de echilibru
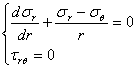(1.14.4)
II.Ecuatiile geometrice:
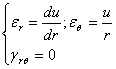(1.14.5)
III.Legea lui Hooke:
(1.14.6)
IV.Expresiile tensiunilor:
(1.14.7)
2.Sa incercam o rezolvare a acestei ecuatii (1.14.3) ;ea poate fi adusa la forma unei ecuatii liniare, omogene cu coeficienti constanti facand substitutia:
sau
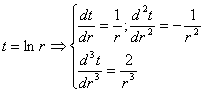(x)
Deci: 
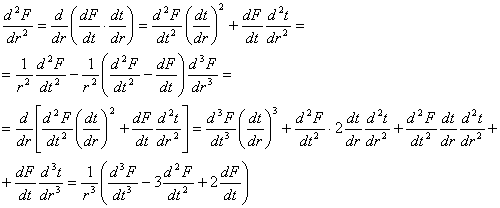
Analog:
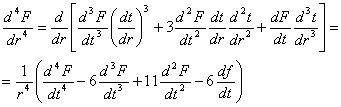
Inlocuind aceste rezultate in (1.14.3) rezulta ecuatia diferentiala de ordinul patru cu coeficienti constanti:
(1.14.8)
Ecuatia caracteristica este:
sau 
care
are doua radacini duble : 
si 
ce corespund la patru integrale particulare
ale ecuatiei:
In acest fel integrala generala a ecuatiei diferentiale (1.14.8) este:
sau
punind 
(1.14.9)
Se pot deci calcula tensiunile
utilizand relatiile (1.14.7):
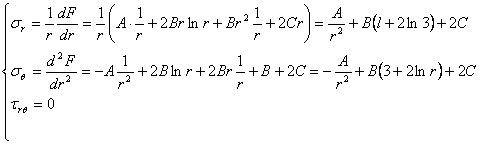
(1.14.10)
In fiecare problema concreta
constantele de integrare vor fi diferite in raport cu conditiile de suprafata
pe care trebuie sa le satisfaca functia F(r) si deci si componentele
tensiunilor 
.
SOLUTIA IN DEPLASARI
3.Solutia obtinuta mai sus a fost exprimata in functie de tensiuni; evident ca putem obtine si o solutie in functie de deplasari.
Vom porni de la legea lui Hooke:
Se rezolva acest sistem de ecuatii
in raport cu si si se obtine forma in tensiuni: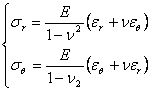
(1.14.11)
Se introduc aici ecuatiile
geometrice (1.14.5):
si se obtine:
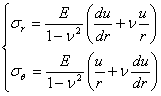(1.14.12)
Analizand acest rezultat se observa ca tensiunile nu sunt independente, ci sunt legate intre ele
prin functia (u). Se poate atunci transforma ecuatia diferentiala de echilibru
in care apar doua functii necunoscute 
intr-o ecuatie diferentiala cu o singura
necunoscuta: u(r).
Pentru cazul particular studiat de noi, am vazut ca ecuatiile diferentiale de echilibru se reduc de fapt la una singura (1.14.4):
(x)
Se calculeaza:
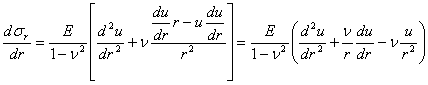
Ecuatia precedenta (x) devine:
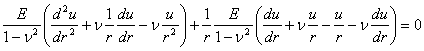
(1.14.13)
Se obtine asa numita " ecuatie diferentiala a deformatiilor" care contine o singura functie necunoscuta u(r). Ea este o ecuatie diferentiala de tip Euler care se rezolva in mod obisnuit facind schimbarea de variabila:
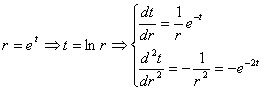
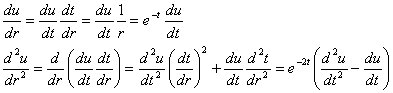
Cu aceste transformari ecuatia (1.14.3) devine:
(1.14.14)
Ecuatia
caracteristica este de forma 
cu solutiile 
si 
Solutia generala va fi de forma:
(1.14.15)
Aceasta este deci solutia problemei noastre in deplasari. Constantele de integrare se determina de asemenea pentru fiecare caz concret in parte punand conditiile pe contur.
|
