Vibratii armonice libere amortizate

Vibratii armonice libere amortizate

Un sistem mecanic aflat in stare de vibratie poseda o energie care-i permite executarea miscarii. Insa orice miscare a unui corp este insotita de pierderi de energie prin frecare intre elementele aflate in miscare relativa (frecare externa), sau prin frecari in interiorul materialelor elementelor elastice ale sistemului (frecare interna). Diminuarea energiei mecanice prin transformarea ei in caldura are ca efect scaderea amplitudinii de oscilatie a corpului oscilant. Acest efect se numeste amortizare a miscarii oscilatorii.

Modelarea matematica a fortelor de frecare este dificila, datorita naturii complexe a fenomenului care le genereaza. Frecarea externa de tip vascos este cea mai raspandita in sistemele mecatronice, iar fortele de frecare de acest tip au fost studiate in mod deosebit. Studiile experimentale au stabilit ca forta de frecare vascoasa este direct proportionala cu viteza relativa dintre corpurile aflate in miscare. Factorul de proportionalitate corespunzator se numeste coeficient de frecare vascoasa, notat c.

Amortizarea interna este determinata de structura moleculara a materialelor care sufera deformatii alternative. Astfel se diferentiaza materiale pentru care amortizarea depinde deopotriva de amplitudinea oscilatiei si de frecventa ei (amortizare vascoelastica), si materiale la care amortizarea depinde numai de amplitudinea vibratiilor (amortizare histeretica).

In cadrul acestei lucrari sunt tratate numai oscilatiile afectate de amortizare vascoasa.

Vibratii armonice de translatie libere amortizate

Se considera sistemul oscilant care include un amortizor vascos, prezentat in figura 2.21.

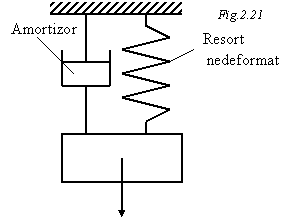
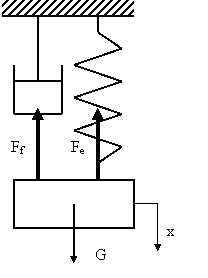
In stare de echilibru static, forta de greutate este echilibrata prin deformarea resortului. O perturbatie exterioara, care poate fi un impuls sau o deplasare a masei sistemului din pozitia de echilibru, imprima sistemului o miscare oscilatorie. Izolarea mecanica a masei concentrate prin inlocuirea legaturilor cu forta elastica, respectiv cu forta de frecare vascoasa a fost reprezentata in figura 2.22. Ecuatia echilibrului dinamic este de forma:

Forta de frecare vascoasa, proportionala cu viteza masei concentrate, se exprima prin relatia:

.

Cu acestea, ecuatia diferentiala a miscarii corpului de masa m este:

Impartind cu m si introducand notatiile

,           ,

ecuatia se rescrie astfel:

Pentru rezolvarea ecuatiei diferentiale se cauta solutii de forma:

unde r este o constanta ce se va determina, iar t este variabila temporala, t > 0. Derivand variabila x succesiv in raport cu timpul se obtin viteza si acceleratia instantanee a corpului analizat:

Inlocuind in ecuatia (2.3) expresiile acceleratiei si vitezei, va rezulta, dupa impartirea ecuatiei prin termenul nenul , o ecuatie de gradul doi, cu necunoscuta r, numita ecuatie caracteristica:

Solutiile acestei ecuatii de gradul doi sunt :

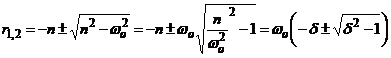
unde reprezinta factorul de amortizare.

Se introduce, de asemenea, coeficientul de amortizare critic, prin expresia :

Cu aceasta noua notatie, factorul de amortizare se poate exprima ca raport adimensional a doi coeficienti de frecare vascoasa :

Comportarea in timp a functiei x(t) ce defineste pozitia in timp a oscilatorului depinde de natura radacini lor r_1,2 si ea va fi discutata in cele ce urmeaza.

Cazul 1. Amortizarea subcritica

Atunci cand factorul de amortizare este subunitar, , radacinile ecuatiei caracteristice sunt complexe:

Solutia generala a ecuatiei diferentiale este:

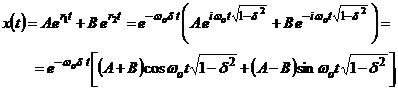
Conform celor aratate prin relatiile (2.10) si (2.11), deplasarea instantanee a corpului care vibreaza se poate exprima sub forma armonica,

Se introduce pulsatia miscarii amortizate,

, iar cu aceasta, deplasarea instantanee este:

Reprezentarea grafica a evolutiei temporale a pozitiei instantanee a unui corp aflat intr-o miscare de oscilatie libera amortizata a fost trasata in figura 2.23.

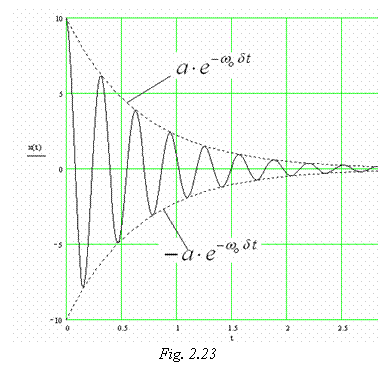
Se observa ca termenul exponential care multiplica functia cosinus, prin prezenta argumentului negativ, are o comportare de apropiere asimptotica de valoarea nula. Aceasta implica o tendinta de diminuare a amplitudinii de oscilatie. Oscilatia, teoretic, nu inceteaza niciodata, dar devine, la un moment dat, practic imperceptibila, datorita evolutiei spre zero a valorii amplitudinii ei. Tendinta de diminuare a amplitudinii depinde de valoarea exponentului negativ al functiei exponentiale.

Daca pulsatia proprie a miscarii oscilatorii libere neamortizate era , pulsatia miscarii amortizate este mai redusa, , ceea ce determina modificarea perioadei de oscilatie a corpului de la valoarea:

,

la o perioada mai ampla, numita pseudoperioada,

.

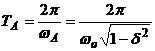Cu alte cuvinte, oscilatiile se produc cu o frecventa mai mica atunci cand in sistem intervine o forta de frecare vascoasa, iar diminuarea frecventei depinde de marimea factorului de amortizare δ. Aceasta frecventa este:

In practica, inginerul doreste sa determine valoare acestui factor de amortizare vascoasa. Pentru aceasta se poate amenaja un stand de masurare a valorilor a doua amplitudini succesive ale miscarii sistemului amortizat studiat, x₁ si x₂.

Raportul celor doua expresii de definesc amplitudinile masurate la un interval de timp egal cu o pseudoperioada rezulta a fi independent de timp:

Faptul ca acest raport nu depinde de timp atrage dupa sine constatarea ca raportul oricaror doua valori ale amplitudinilor succesive este un raport constant, daca miscarea oscilatorie este amortizata vascos:

,

unde x_n defineste a n-a amplitudine masurata.

Logaritmul natural al acestui raport constant se numeste decrement logaritmic al amortizarii:

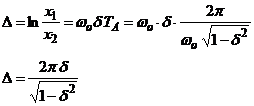
Din aceasta ultima relatie se poate evalua factorul de amortizare δ,

.

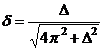Prin urmare, cu ajutorul standului experimental se masoara doua amplitudini succesive in cursul executarii miscarii oscilatorii, iar logaritmul natural al valorii raportului amplitudinilor, notat Δ, permite calculul factorului de amortizare δ. Insa δ a fost definit in functie de coeficientul de amortizare vascoasa, , astfel ca prin evaluarea lui se poate stabili prin calcul direct valoarea coeficientului de frecare vascoasa c.

Daca sistemele de ungere utilizate in practica au viscozitate redusa, amortizarea este slaba. Aceasta se exprima matematic prin aproximarea:

Se observa ca aceasta atrage dupa sine o expresie mai simpla a decrementului logaritmic:

Cazul II. Amortizarea supracritica

Atunci cand factorul de amortizare , radacinile ecuatiei caracteristice sunt reale si distincte:

Solutia generala a ecuatiei diferentiale este:

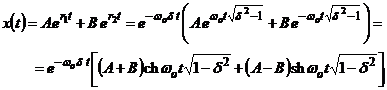
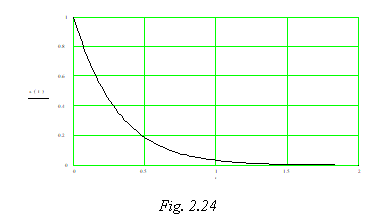
Deplasarea instantanee a corpului care vibreaza nu se mai poate exprima sub forma armonica. Graficul evolutiei in timp a acestei marimi (fig. 2.24) evidentiaza o comportare asimptotica a pozitiei instantanee a corpului catre valoarea zero.

Cazul III. Amortizarea critica

In cazul in care , ecuatia caracteristica are doua radacini reale si egale,

Solutia generala a ecuatiei diferentiale a miscarii oscilatorii va avea forma:

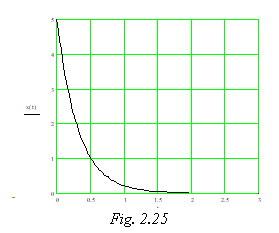
Reprezentarea grafica a unei astfel de functii se poate vedea in figura 2.25.

Amortizarea critica reprezinta limita miscarii periodice, ceea ce semnifica faptul ca acel corp ce a fost deplasat este readus la echilibru in cel mai scurt timp cu putinta si fara sa execute oscilatii. Multe dispozitive, in special cele electrice, sunt amortizate critic pentru a beneficia de aceasta proprietate.

Exemplul

Un sistem aflat in stare de vibratie a fost masurat si s-a constatat ca amplitudinile a doua oscilatii succesive sunt egale cu 2,5 mm si 0,5 mm. Sa se calculeze decrementul logaritmic al amortizarii si factorul de amortizare vascoasa.

Rezolvare:

Conform definitiei, decrementul logaritmic este:

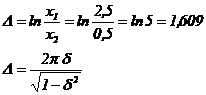
Decrementul logaritmic se exprima cu ajutorul factorului de amortizare δ astfel:

Aceasta relatie poate fi privita ca o ecuatie cu necunoscuta δ, care se reolva prin ridicarea la patrat a ambilor ei termeni. Se obtine

,

astfel ca factorul de amortizare va fi:

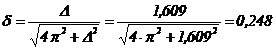
Exemplul

O masa de 5 kg este suspendata de un resort si i se imprima o miscare oscilatorie libera. Se constata ca amplitudinea se reduce la 10% din valoarea ei initiala dupa 3 oscilatii, pe care le efectueaza in 0,6 secunde. Sa se determine:

factorul de amortizare

pulsatia proprie a anasamblului neamortizat

pulsatia miscarii amortizate

rigiditatea arcului

coeficientul critic de frecare vascoasa

coeficientul efectiv de frecare vascoasa

Rezolvare:

Din enunt reiese ca x₃ = 0,1.x₁. Se poate scrie ca:

Dar,

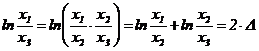
Prin urmare,

, adica

Folosind rezultatul obtinut in exemplul anterior, 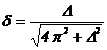, se poate stabili valoarea factorului de amortizare:

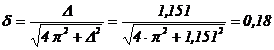
Din faptul ca sistemul executa 3 oscilatii in 0,6 secunde, se poate stabili pseudoperioada miscarii amortizate:

Stiind ca 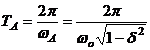, se poate evalua pulsatia proprie a sistemului,

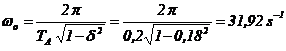
Pulsatia miscarii amortizate de stabileste tot cu ajutorul pseudoperioadei T_A,

Rigiditatea arcului determina, impreuna cu masa corpului, valoarea pulsatiei proprii, prin relatia de definitie . Astfel ca rigiditatea se exprima prin:

Coeficientul critic de frecare vascoasa a fost definit cu relatia . Valoarea lui este in cazul acestei aplicatii:

Factorul de amortizare s-a exprimat prin raportul . De aici se evalueaza valoarea coeficientului de frecare vascoasa c, celelelte doua marimi fiind stabilite anterior:

Studiul locului geometric al radacinilor ecuatiei caracteristice (cazul amortizarii vascoase)

Adesea este utila analiza dependentei radacinilor ecuatiei caractersitice de parametrul δ>0. Dupa cum s-a vazut, aceste radacini sunt:

, daca   

, daca           

Aceste radacini pot fi reprezentate intr-un sistem de axe ortogonale in care pe axa absciselor se reprezinta partea reala a rapor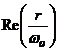tului , , iar pe axa ordonatelor se reprezinta partea imaginara a raportului , 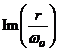. Deoarece fiecarei valori δ ii corespund doua valori , la reprezentarea radacinilor se evidentiaza doua locuri geometrice, dupa cum se poate vedea in figura 2.23.

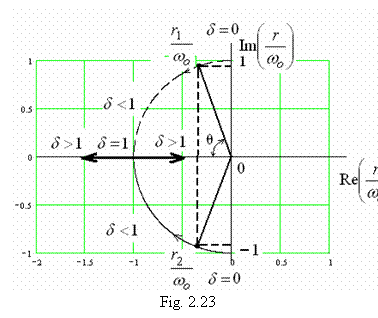
Pozitia unei radacini in planul (r/ω) frecventa de oscilatie (axa Im(r/ω)) a sistemului, daca exista o frecventa nenula, precum si viteza de crestere sau descrestere a oscilatiei (axa Re(r/ω)).

Deoarece axa Re(r/ω) este negativa in partea stanga a axei Im(r/ω), toate radacinile situate la stanga axei Im(r/ω) descriu o oscilatie cu amplitudine descrescatoare, specifica unui sistem stabil. In schimb, radacinile situate la dreapta axei Im(r/ω) descriu o oscilatie cu amplitudine crescatoare, specifica unui sistem instabil.

Acest studiu al locului geometric al radacinilor este util in proiectarea echipamentelor, deoarece evidentiaza imediat efectele modificarii coeficientului de frecare asupra raspunsului sistemului. De asemenea, el este necesar in studiul controlului dinamicii sistemului. Trebuie remarcat faptul ca factorul de amortizare δ este egal cu cosθ in figura 2.23.

Vibratii armonice de rotatie libere amortizate

Se considera acelasi sistem oscilant din figura 2.8, in care s-a atasat volantului un amortizor cu palete, care sunt sufundate intr-un vas plin cu lichid vascos. Ansamblul a fost reprezentat in figura 2.26. La rotirea discului cu unghiul θ in sens trigonometric, asupra discului, prezentat izolat, dupa ruperea legaturilor, in figura 2.27, asupra discului actioneaza momentul de torsiune elastic al barei de suspensie si momentul de frecare generat de amortizorul vascos, orientate in sens orar. Ele sunt achilibrate de momentul cinetic, conform ecuatiei:

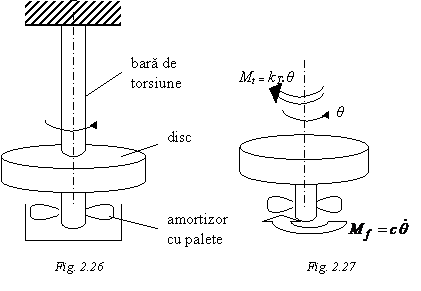
Amortizorul vibratiilor torsionale este un rotor cu palete, care se  roteste in interiorul unui cilindru cu ulei. Momentul de frecare este

Decrementul logaritmic al miscarii este:

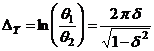
Ceilalti parametri ai miscarii sunt similari oscilatiilor de translatie, prezentati in paragraful 2.

Circuite electrice in regim armonic. Oscilatii libere amortizate

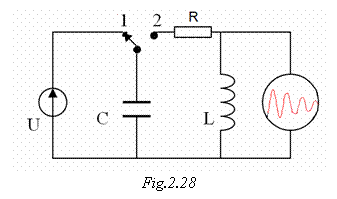
Se considera circuitul din figura 2.24, care este similar celui reprezentat in figura 2.28, dar in care s-a inclus un rezistor cu rezistenta egala cu R. Aceasta valoare a rezistentei poate include sau nu rezistenta sarmei din care este confectionata bobina. Generatorul electric cu tensiune constanta U incarca un condensator cu capacitate C, cand intrerupatorul este inchis pe pozitia 1. Dupa finalizarea incarcarii condensatorului cu sarcina electrica, intrerupatorul este deplasat pe pozitia 2. Sarcina acumulata pe armaturi se descarca prin bobina de inductanta L. Daca se conecteaza in paralel cu acest circuit bobina-condensator un osciloscop, pe ecranul acestuia se va putea vedea evolutia in timp a curentului in circuit ca in figura 2.28.

Din teoria circuitelor electrice, se cunoaste ca ecuatia de tensiuni pentru circuitul format din condensatorul C si bobina L este:

Aceasta ecuatie integro-diferentiala se poate reformula prin inlocuirea curentului instantaneu i(t) cu necunoscuta q(t), sarcina acumulata pe armaturile condensatorului la momentul t. Se stie ca:

, sau .

Cu acestea, ecuatia diferentiala ce descrie functionarea circuitului va capata forma:

In urma impartirii la valoarea inductantei L, se obtine:

Similar sistemelor mecanice, se definesc:

si

Factorul de amortizare δ al circuitului electric este prezent datorita existentei unei rezistente electrice R a circuitului:

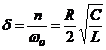
In literatura, circuitele electrice in regim armonic sunt caracterizate de factorul de calitate, definit prin:

.

Se poate observa ca intre factorul de amortizare δ al circuitului si factorul de calitate exista relatia:

.

Conform relatiei (>>>>>>>>>>>>>), decrementul logaritmic al circuitului va fi calculat cu ajutorul factorului de amortizare al circuitului electric:

Exprimand decrementul logaritmic cu ajutorul factorului de calitate Q, vom deduce formula:

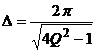
In analogie cu sistemul oscilant mecanic, pulsatia proprie a circuitului electric serie va fi:

w_o

Analogii intre circuitele electrice si sistemele oscilante mecanice amortizate

Ecuatia diferentiala a carei solutie este pozitia momentana x(t) a corpului punctiform de masa m care este legat elastic de un perete rigid, iar miscarea lui determina aparitia unei forte de frecare vascoasa are expresia, stabilita anterior:

Sarcina de pe armaturile unui condensator de capacitate C, element al unui circuit oscilant ce mai cuprinde o bobina de inductanta L, precum si un rezistor de rezistenta electrica R este solutie a unei ecuatii asemanatoare:

Similitudinea formala intre cele doua ecuatii a permis introducerea unei analogii intre sistemele oscilante electrice si sistemele mecanice oscilante, constituite din mase concentrate. Acest lucru a fost constatat si dezvoltat in paragraful 4. In plus se mai poate remarca termenul care are ca efect disiparea energiei de oscilatie. Acesta este introdus prin coeficientul c de frecare vascoasa, in cazul sistemului mecanic, respectiv prin rezistenta electrica R, in sistemul oscilant electric. Cu aceasta, tabelul 2.1 se poate complecta cu o noua linie:

Tabel 2.2: Analogii intre marimile sistemelor oscilante de tip mecanic si electric

Energia disipata prin amortizare

Energia disipata intr-un ciclu de oscilatie datorita fortei de frecare vascoasa, intr-un sistem vibrator cu un singur grad de libertate este aproximativ egal cu:

Daca atunci . Cu acestea, energia disipata va fi:

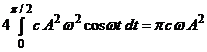
Exemplul

Un sistem vibrator cu un grad de libertate are factorul de amortizare δ = 0,02. Sa se evalueze energia disipata pe un ciclu de oscilatie, relativ la energia sistemului la inceputul miscarii oscilatorii. Sa se determine amplitudinea celei de-a zecea oscilatii, daca a patra oscilatie are amplitudinea de 3 mm.

Rezolvare:

Energia sistemului la inceputul primei oscilatii este egala cu energia potentiala de deformatie a resortului a carui sageata este egala cu amplitudinea x₁, iar energia sistemului la sfarsitul primei oscilatii coincide cu energia la inceputul celei de-a doua oscilatii, la momentul in care resortul este deformat cu valoarea amplitudinii x₂.

Energia la debutul ciclului =

Energia la finele ciclului =

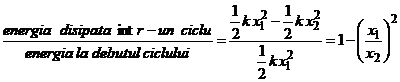
Raportul amplitudinilor se poate evalua prin intermediul decrementului logaritmic:

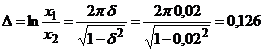
Raportul amplitudinilor va fi:

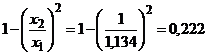
Rezultatul indica faptul ca in cursul unei oscilatii se disipa 22,2% din energia existenta in sistemul oscilant la incepului acelei oscialtii. Trebuie remarcat ca acest raport este independent de timp, adica in curcsul oricarei oscilatii se va disipa un procent egal cu din energia oscilatiei precedente.