Integrale definite

Integrale definite

IV.1. Definitia integrabilitătii (integrale Riemann)

Notatii: f:[a,b] R, D = (a = x₀, x₁, x₂, ., x_n = n) diviziune, x_i-1 x_i x_i , x_i - puncte intermediare, s_D(f, x) - suma Riemann:

Definitia VI.1.1. f se numeste integrabilă dacă există numărul real I_f cu proprietatea: "e > 0, h_e >0 astfel încâtr pentru orice divizune D a lui [a,b] cu si orice puncte intermediare x_i are loc unde

Se notează:

Proprietăti ale integralei definite:

;

;

;

.

Formula lui Leibniz-Newton:

(F - primitivă a lui f)

Teorema de medie:

Dacă f continuă pe [a,b], atunci x [a,b] astfel încât:

Formula de integrare prin părti:

Formula de schimbare de variabilă:

Dacă j :[a,b] J, f:J R, f continuă pe J, j derivabilă cu derivata continuă pe [a,b], atunci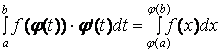

Proprietăti de paritate:

Dacă f:[-a,a] R continuă atunci: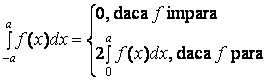

VI.2. Aplicatii ale integralei definite

Aria subgraficului G_f, f:[a,b] R₊, f continuă:

y

aria G_f

y

0 a b x

Aria subgraficului G_f,g, f,g:[a,b] R si

f(x) g(x) " x [a,b]

0 a G_f,g b x

aria

Volumul corpurilor de rotatie, f:[a,b] R₊, f continuă:

y

a b x

z

3. Lungimea graficului f:[a,b] R₊, f derivabilă cu derivata continuă:

B

A

a b

4. Aria suprafetelor de rotatie:
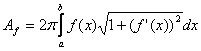