MULTIMI, ELEMENTE DE LOGICA

MULTIMI ,ELEMENTE DE LOGICA

Multimea numerelor reale: operatii algebrice cu numere reale, ordonarea numerelor reale, modulul unui numar real, aproximari prin lipsa sau prin adaos , partea intreaga, partea fractionara a unui numar real; operatii cu intervale de numere reale. 454e47e

Tipuri de rationamente logice: inductia matematica. Probleme de numarare.

NZQR

Modulul unui numar real

Ecuatii cu modul

exemple :1) sa se rezolve ecuatia

explicitatrea modului se poate face folosind semnul expresiei din modul

cazul I daca ec devine -(x+3)=2x-1 cu sol x=dar

cazul II daca ecuatia devine x+3=2x-1 cu sol x=4

deci singura solutie este 4

exemplu 2:sa se rezolve ecuatia

explicitatrea modului se poate face folosind semnul expresiei din modul

cazul I daca ec devine cu sol x=1dar

cazul II daca ecuatia devine

rezulta cu sol doar

cazul III daca ec devine cu sol x=1dar

cazul IV daca ec devine cu sol x=-2dar

deci singura solutie este x=1

Inecuatii cu modul

eplicitam modulele din tabelul cu semne

cazul 1 daca inec devine rezulta cu sol deci solutia cazului 1 este deci

cazul 2 daca inecuatia devine

rezulta cu sol deci solutia cazului 2 este deci

cazul 3 daca ec devine rezulta

cu sol deci solutia cazului 2 este deci

solutia finala este

Aproximarea prin lipsa si prin adaos

Numarul rational rezultat prin eliminarea tuturor zecimalelor unui numar real pozitiv,incepand de la o zecimala zecimala oarecare spre dreapta se numeste aproximare prin lipsa a numarului

Numarul rational rezultat dintr-o aproximare prin lipsa ,caruia i se mareste cu 1 ultima cifra se numeste aproximarea prin adaos a numarului

exemplu:a=10,2387 aproximari prin lipsa 10 ; 10,2 ;10,23 ;10,238

aproximari prin adaos 11 ; 10,3 ;10,24 ;10,239

Partea intreaga, partea fractionara a unui numar real

partea intreaga a unui numar real ,notata [a] este cel mai mare numar intreg mai mic sau egal cu a

deci daca si

Observatii:1)Inegalitatea mai poate fi scisa

2)daca oricare

3) daca si atunci

parte fractionara a unui numar real x notata este =x-[x]

Obsevatii 1) oricare x real

2) daca si atunci

Ecuatii cu parte intraga

pentru rezolvarea ecuatiilor de forma [f(x)]=g(x) procedam astfel:

-notez partea intreaga cu n

-inlocuim in ecuatie partea intraga in ecuatie cu n si scot pe x in functie de n

- scriu inegalitatea partii intregi: (inlocuind pe a cu expresia ce o avem in parte intreaga)

-in inegalitatea partii intregi inlocuim totul infunctie de n

- rezolv sistemul obtinut cu necunoscuta n, iese nunui interval dar n este intreg deci luam doar intregii apartinand acelui interval

-aflu pe n dupa care inlocuind il aflu si pe x

Exemplu:

notez deci

inegalitate dubla de mai sus devine echivalenta cu sistemul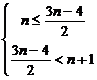

devine iese dar n e intreg deci n ar puta fi 5 sau 4

daca n=5 x=12 daca n=4 x=9

Inductie

Notam cu P(n) afirmatia ce trebuie demonstrata

Dc zice n a verific P(a) (de obicei este P(1) sau P(0) )

P(n) P(n+1) presupun P(n) adevarat si demonstrez P(n+1)

Exemplu: fie A= sa se calculeze Aⁿ

Calculez A²= A³= A⁴= observ Aⁿ=

Tot ceea ce observam trebuie dem prin inductie

P(n): Aⁿ= P(1): A¹= adevarat

P(n) P(n+1) presupun P(n) adevarat si demonstrez P(n+1)

P(n): Aⁿ⁺¹= Aⁿ⁺¹=Aⁿ A== ceea ce trebuia demT Aⁿ=