MULTIMI PARTIAL ORDONATE

MULŢIMI PARŢIAL ORDONATE

Introducerea......

I.1. Generalitati despre multimi partial ordonate.

O ordine partiala este o relatie binara R peste o multime D care este reflexiva, antisimetrica si tranzitiva, adica oricare ar fi avem :

- (reflexivitate)

- daca si atunci (antisimetrie)

- daca si atunci (tranzitivitate)

O multime D cu o ordine partiala, notata , se numeste multime partial ordonata; se noteaza cu . Relatia R aici se introduce prin , adica este notat cu .

Exemple de multimi partial ordonate :

a)     (N, )

b)    (N, | )

c)     Fie A o multime, P A multimea partilor lui A si incluziunea atunci (P A), ) este multime partial ordonata.

d)    Daca este o multime partial ordonata si atunci restrictia relatiei la B îi confera acesteia o structura de multime partial ordonata.

Fie D o multime partial ordonata , A submultime a lui D.

Definim

A se numeste multime superioara daca .

Definim

A se numeste multime inferioara daca .

Exemple I.1.1

Daca se considera P A), ) si multimile A P A), atunci A formata din toate supramultimile multimilor din A inclusive aceasta; A este formata din toate submultimile multimilor din A inclusive aceasta.

Fie cu ordonarea produs a ordonarilor naturale din cele doua intervale: daca si . Aceasta este o relatie de ordine partiala.

Daca este o functie, atunci , graficul functiei este o submultime a multimii D.

Aici , iar

ultima multime fiind numita si subgraficul lui f.

În aceasta multime se pot evidentia si alte multimi, sa fixam si .

Primele doua multimi sunt multimi superioare iar celelalte doua sunt multimi inferioare.

Consideram o multime partial ordonata D, cum este descrisa în figura alaturata. Ea este formata din puncte din , ordonarea fiind si aici ordonarea produs, mai precis restrictia ordonarii la aceasta multime.

Fig. 1.1

Multimea A din figura 1.2, deci ramura din dreapta începând de la punctul , dar fara acesta este o multime superioara.

Fig. 1.2

Daca îi adaugam însa punctual si notam cu multimea obtinuta, atunci nu mai este multime superioara. Presupunem ca contine si partea din stânga, simetrica cu cea din împreuna cu punctul , adica este multimea din figura 1.3, care nu mai coincide cu .

Fig. 1.3

Fie multime partial ordonata.este multime dirijata (la dreapta) daca oricare ar fi exista astfel încât si .

Fie multime partial ordonata,submultime a acesteia. Supremul lui S este un element astfel încât

a) , oricare ar fi

b) oricare ar fi astfel încât , oricare ar fi avem

Supremul este unic. Într-adevar, daca îndeplinesc cele doua conditii pentru S atunci , si este antisimetrica obtinem .

O multime partial ordonata D se numeste complet dirijata, prescurtat POCD, daca in ea fiecare submultime dirijata , are supremum, notat sau .

I.2. Relatia "mult mai jos" în multimi partial ordonate

Fie , va însemna ca pentru orice multime dirijata cu , atunci exista astfel încât .

Pentru orice notam

Pentru o multime

Fie D multime partial ordonata. D este continua daca este multime dirijata si , oricare ar fi .

Daca D este simultan latice completa si multime POCD continua atunci se numeste latice continua.

Un element este compact daca , adica, daca unde E este multime dirijata, atunci pentru un .

Propozitie I.2.1  Daca rezulta .

Demonstratie: Daca si consideram , atunci E este dirijata si rezulta . ■

Propozitie I.2.2 Fie D o multime POCD, elemente cu proprietatile , si atunci .

Demonstratie: Fie E o multime dirijata cu atunci si rezulta ca exista un astfel încât deci si atunci rezulta ca . ■

Propozitie I.2.3 Fie D o multime POCD continua, elemente din D astfel încât , . Atunci exista , astfel încât si .

Demonstratie Fie , este multime continua. Atunci este multime dirijata si

Din , rezulta ca , cum este multime dirijata rezulta ca exista un astfel încât , . Cum obtinem . ■

Propozitie I.2.4 (Proprietatea de interpolare) Fie o multime POCD continua, elemente din cu . Atunci exista astfel încât .

Demonstratie Fie , este multime continua. Atunci este multime dirijata si

Din si rezulta ca exista astfel încât (1). Cum si este multime dirijata rezulta .

Fie , si este multime dirijata exista rezulta , deci obtinem (2). Din (1),(2) obtinem . ■

Propozitie I.2.5. Fie o multime POCD si elment din . Atunci notam cu cel mai mic element, daca exista, si .

Demonstratie Presupunem ca exista cel mai mic element , atunci si exista astfel încât , conform definitiei obtinem . ■

Propozitie I.2.6 Fie o multime POCD si elemente din . Daca si atunci rezulta .

Demonstratie: Fie D multime dirijata, atunci exista astfel încât de unde rezulta ca atunci exista astfel încât , obtinem . ■

Fie L o multime nevida si o relatie binara. o numim structura relationala.

Daca R este reflexiva, adica oricare ar fi , notat de obicei , atunci vorbim de o structura relationala reflexiva. Corespunzator vorbim de o structura relationala antisimetrica, daca relatia R este antisimetrica, adica si implica , respectiv structura relationala tranzitiva daca relatia R este tranzitiva, adica si implica .

Propozitie I.2.7 Fie o structura relationala reflexiva si elemente din . Atunci daca si numai daca .

Propozitie I.2.8 Fie o structura relationala reflexiva si antisimetrica, element din . Atunci oricare ar fi avem .

Demonstratie Daca atunci conform definitiei rezulta de unde obtinem . ■

Propozitie I.2.9 Fie o structura relationala reflexiva si antisimetrica, element din . Atunci si .

Propozitie I.2.10 Fie o structura relationala reflexiva si tranzitiva, elemente din . Daca , atunci si .

Demonstratie Daca rezulta si cum atunci de unde obtinem , deci .

Daca atunci , rezulta ca si , deci rezulta . ■

Fie o structura relationala reflexiva, antisimetrca si marginita inferior, un element din . Atunci se poate observa ca multimea nu este vida.

Daca este structura relationala tranzitiva si un element din .

Atunci

este multime inferioara

si

este multime superioara.

Propozitie I.2.11 Fie L un lant sup-complet si elemente din . Daca nu este compact si atunci .

Demonstratie Daca nu este compact atunci .

Presupunem atunci , contradictie cu nu este compact, deci . ■

Propozitie I.2.12 Fie o structura relationala reflexiva, antisimetrica si marginita inferior atunci este compact.

Demonstratie: Fie . atunci exista astfel încât , dar de unde rezulta ca deci este compact.

Fie o structura relationala si un element din . Elementele din multimea formeaza o submultime a lui definita astfel

Elementele din multimea formeaza o submultime a lui definita astfel

Propozitie I.2.13 Fie o structura relationala si ,elemente din . Atunci daca si numai daca .

Demonstratie Daca , atunci conform definitiei rezulta .

Reciproc, daca atunci rezulta . ■

Propozitie I.2.14 Fie o structura relationala si elemente din . Atunci daca si numai daca .

Demonstratie: Daca rezulta . Reciproc, daca atunci rezulta . ■

Propozitie I.2.15 Fie o structura relationala reflexiva si antisimetrica si elemente din . Daca atunci .

Demonstratie Daca atunci de unde rezulta ca . ■

Propozitie I.2.16 Fie o structura relationala reflexiva si antisimetrica, elemente din . Daca atunci .

Demonstratie Daca atunci de unde obtinem ca . ■

Propozitie I.2.17 Fie o structura relationala tranzitiva si elemente din . Daca atunci .

Demonstratie Fie atunci rezulta si cum rezulta , deci . ■

Propozitie I.2.18 Fie o structura relationala tranzitiva si elemente din . Daca atunci .

Demonstratie Daca rezulta si cum obtinem de unde rezulta ca . ■

Un POCD este algebric daca fiecare element este supremumul unei multimi dirijate de elemente compacte. Pentru simplitatea exprimarii se va spune ca fiecare element este un supremum dirijat de elemente compacte.

Alternativ, POCD-urile algebrice sunt numite domenii.

Daca un domeniu ( adica un POCD algebric ) este latice completa atunci se numeste latice algebrica.

Teorema I.2.1 Fie domeniu echivalent cu este POCD algebric adica oricare ar fi , , elemente compacte, multime dirijata. Atunci este POCD continu.

Demonstratie Fie atunci , elemente compacte, multime dirijata rezulta ca , si de unde rezulta ca , deci atunci rezulta adica este POCD continu. ■

Teorema I.2.2 Într-un POCD algebric relatia este caracterizata de daca si numai daca exista un element compact astfel încât .

Demonstratie Presupunem ca atunci unde este compact, multime dirijata. rezulta ca exista compact astfel încât .

Reciproc, presupunem , compact rezulta, si atunci . ■

este baza numarabila pentru un POCD continu sau se poate spune ca POCD este cu baza numarabila daca exista o submultime a lui , unde este cel mult numarabila, astfel încât pentru elemente din avem rezulta atunci ca exista astfel încât .

Teorema I.2.3 Un POCD algebric are baza numarabila daca si numai daca multimea elementelor compacte este numarabila.

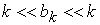Demonstratie Daca presupunem ca POCD este algebric cu baza numarabila de elemente compacte, cum pentru orice element compact , are loc , prin ipoteza ar exista astfel încât . Pentru elemente compacte rezulta atunci (daca avem rezulta (1) ; dar rezulta (2). Din (1) si (2) rezulta contradictie cu ipoteza )

Reciproc, presupunem ca exista o infinitate numarabila de elemente compacte.

este algebric rezulta ca oricare ar fi , exista compact astfel încât , dar rezulta rezulta ca . Din rezulta . Prin urmare atunci multimea elementelor compacte este baza numarabila. ■

I.3. Relatia " mult mai jos " în spatii topologice.

Fie spatiu topologic, familia multimilor deschise atunci este latice în raport cu incluziunea , si fie . Atunci înseamna ca pentru oricare acoperire deschisa a lui exista o subfamilie finita a acestei acoperiri care acopera . În aceasta situatie este potrivit sa spunem ca este compact în .

Fie , si fie o acoperire cu multimi deschise a lui . Proprietatiile relatiei nu pot fi aplicate direct lui deoarece nu este dirijata. Aceasta familie poate fi transformata usor într-o famile dirijata.

Mai precis fie familia tuturor reuniunilor finite de multimi din . Atunci este evident dirijata în raport cu incluyiunea , deoarece pentru doua reuniuni finite arbitrare de multimi din reuniunea acestora este tot o reuniune finita de elemente din care include fiecare din reuniunile din care este formata.

În plus se observa rezulta ca si este o acoperire cu multimi deschise a multimii si în plus este dirijata.

Din definitia relatiei rezulta atunci ca exista un element din care contine , adica exista o subacoperire finita a lui a multimii .

Reciproc, presupunem ca în orice acoperire deschisa a lui exista un numar finit de elemente a caror reuniune contine (acopera) .

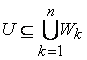Fie o acoperire deschisa a lui care este si dirijata. Conform ipotezei exista un numar finit de multimi în astfel încât , dar este si dirijata de aici rezulta ca exista astfel încât , dar atunci si rezulta .

Se spune ca este nucleu compact daca pentru si exista o multime deschisa cu si compact in .

este nucleu compact daca si numai daca oricare ar fi exista un sistem fundamental de vecinatati deschise si compacte.

Teorema I.3.1 este nucleu compact daca si numai daca este o latice continua.

Demonstratie Presupunem ca X este nucleu compact.

Fie G deschis atunci

Aratam ca .

Evident

Fie . Pentru ca este nucleu compact rezulta ca exista deschisa cu si .

rezulta deci .

Reciproc, presupunem latice continua adica oricare ar fi

Daca rezulta ca exista deschis cu si atunci rezulta este nucleu compact. ■

înseamna ca exista o multime compacta astfel încât . Daca este o acoperire deschisa pentru , atunci este o acoperire deschisa pentru , deci contine o subacoperire finita a acesteia, care va fi acoperire finita si pentru , deci .

Teorema I.3.2 Topologia unui spatiu local compact este o latice distributiva continua in care daca si numai daca .

Demonstratie Într-un spatiu local compact are loc si relatia deoarece compactitatea locala înseamna aici ca orice punct are un sistem fundamental de vecinatati compacte.

Ultima reuniune este dirijata care poate fi deci folosita in definitia lui care ne da 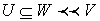pentru un W, atunci . Prin urmare daca si numai daca . ■

Un spatiu este local compact daca pentru orice multime deschisa si orice cu exista o multime deschisa si o multime compacta , astfel încât . Aceasta se exprima echivalent prin a spune ca orice vecinatate compacta a acestui punct, adica orice punct al spatiului poseda un sistem fundamental de vecinatati .

În aceasta proprietate se poate înlocuii punctul cu o multime compacta. Mai precis, daca este local compact, este o multime compacta si o multime deschisa cu , atunci exista o multime deschisa si una compacta astfel încât .

Într-adevar, sa pornim de la . Pentru fiecare exista o multime deschisa si una compacta , astfel încât si .

Rezulta este o acoperire deschisa a lui . Din ea se poate extrage o subacoperire finita a lui .

Fie atunci 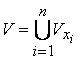si . Rezulta ca este multime deschisa si este multime compacta (o reuniune finita de multimi compacte este evident compacta

În concluzie rezulta .