PRINCIPIUL INCLUDERII SI AL EXCLUDERII

PRINCIPIUL INCLUDERII SI AL EXCLUDERII

Teorema (Principiul includerii si al excluderii)

Fiind date n multimi finite 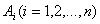si, notand cu numarul de elemente din multimea atunci:

(1 .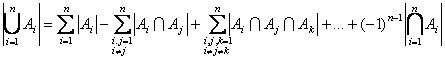

Demonstratie .Vom demonstra formula (1) prin inductie matematica dupa n.

Pentru , avem de demonstrat ca : .

Intr-adevar numarul elementelor reuniunii multimilor si , din care se scade numarul elementelor commune multimilor si care au fost numarate de doua ori .

Sa prsupunem formula (1) adevarata pentru n si s-o demonstram pentru avem:

, deci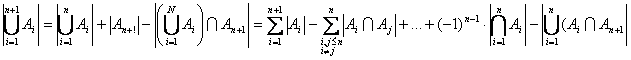

Aplicand formula (1) pentru , tinand seama ca , etc. obtinem:

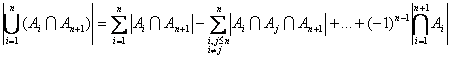de unde tinand seama de relatia de mai sus rezulta

.

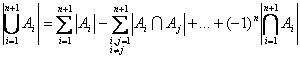Aplicatii :

1.Cate numere naturale mai mici sau egale cu 1000 sunt divizibile cu 2 sau cu 3 sau cu 5 .

Solutie. Fie ;

si .

Se observa ca .

Evident numarul cautat este Aplicand principiul includerii si excluderii

1.

2. Fie E o multime cu elemente ,iar F o multime cu elemente .Cate elemente are

multimea

Solutie . Putem considera prin aceasta notatie pastram numai indicii elementelor din cele doua multimi fara a intelege de exemplu ca elementul 1 este comun multimilor si .

Se stie ca: are elemente .

Daca functia este injectiva atunci si numarul fuctiilor injective de la la

Este egal cu . Daca este bijectiva atunci si numarul functiilor bijective de la la ,cu ,este egal cu .

Pentru a calcula numarul functiilor surjective definite pe cu valori in (in care caz ),

vom aplica principiul includerii si excluderii.

Numarul functiilor surjective de la la este egal cu diferenta dintre numarul al tuturor functiilor definite pe cu valori in si numarul s al functiilor nesurjective de la la .

Pentru fiecare sa notam

.

Avem , unde .

Aplicand formula (1) obtinem :

Dar este multimea functiilor definite pe cu valori in , deci in

Este multimea functiilor definite pe cu valori in , deci si in general unde si pentru orice

2.

Observam ca 0/.

Deci termenii apar in suma respectiva de ori deci :
.

Deci numarul al functiilor surjective de la pe este egal cu :

(2)

Observatie. Cu un caz particular al egalitatii (2) obtinem identitatea :

(3)

PROBLEME

Cate numere naturale mai mici sau egale cu 1000 nu se divid nici cu 2 nici cu 3 nici cu 5

Cum 734 de numere se divid fie cu 2 fie cu 3 fie cu 5 (conf. aplicatiei 1) 1000- 734=266

nu se divid nici cu 2 nici cu 3 nici cu 5.

Sa se afle in cate moduri se pot imparti 5 abiecte distincte la 3 persoane cu conditia ca fiecare persoana sa primeasca cel putin un obiect

Numarul cautat este egal cu numarul functiilor surjective pe o multime cu 5 elemente intr o multime cu 3 elemente , deci este egala cu :

3.fiind date n puncte in plan care se unesc itre ele prin segmente sa se demonstreze ca daca nu exista nici un triunghi cu varfurile in cele n puncte , atunci exista cel putin un punct care este extremitatea a cel mult .

Intr-adevar , pentru un punct notat fie multimea punctelor legate cu printr-un segment si sa presupunem prin absurd ca pentru orice unde cu am notat multimea celor n puncte din plan .

Sa alegem un punct si in multimea sa alegem un punct

3.

Avem , deoarece

Dar deci exista aceasta multime continand cel putin un element .

Am ajuns insa la o contradictie deoarece sunt virfurile unui triunghi si noi am presupus ca nu exista cu virfurile in puctele X

Deci exista un punct asa ca .

4.Sa se demonstreze ca puncte situate in plan pot fi unite prin cel mult segmente de dreapta , astfel incat sa nu formeze nici un triunghi cu varfurile in aceste puncte .

Vom demonstra problema prin inductie dupa .

Pentru n=1 sau n=2 rezultatul este imediat deoarece in primul caz numarul segmentelor este egal cu zero , iar in al doilea caz el este egal cu 1 .

Sa presupunem problema adevarata pentru puncte si s o demonstram pentru

Am vazut ca exista un punct cu care este extremitate a cel mult segmente .

Dar multimea de puncte poate fi uita prin cel mult segmente astfel incat san u formeze nici un triunghi cu varfurile in aceste puncte deci numarul total de segmente care

unesc punctele din multimea (cu n+1 puncte ) este majorat de 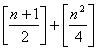Vom demonstra ca acest numar este egal cu : .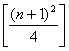

Intr-adevar fie ,cu

Atunci 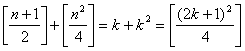, deoarece evident

4.

Daca cu atunci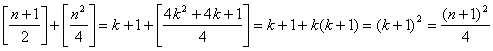

Deci aratam ca :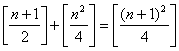 si cu aceasta demonstratia este gata.

Observatie. Pentru a obtine exact segmente de dreapta intre cele puncte asfel incat sa

nu se formeze nici un triuhnghi cu varfurile in aceste puncte , se poate proceda astfel : se grupeaza cele puncte in doua clase care contin respectiv si puncte si uneste fiecare punct cu toate punctele care nu apartin undei aceleasi clase cu el .

5. Fie numar natural .Sa se gaseasca o formula pentru determinarea lui .

Sa scriem descompunerea lui in factori primi si sa notam cu multimea

numerelor naturale mai mici sau egale cu care sint multipli de

Obtinem .

Pentru a obtine numaul numerelor naturale mai mici sau egale cu care sint prime cu , trebuie sa scadem din numarul numerelor naturale mai mici sau egale cu numarul numerelor mai mici sau egale cu care nu sunt prime nu , adica apartin multimii .

Deci

Dind factor comun pe , observam ca ceea ce ramine este tocmai

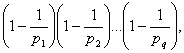deci

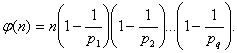
5.

6. Fie un numar natural iar o permutare a multimii . Spunem ca permutarea admite o coincidenta in daca . Sa se gaseasca numarul al permutarilor de

Obiecte fara coincidente.

Sa notam cu multimea celor permutari care admit o coincidenta in si sa aplicam

Principiul includerii si al excluderii pentru a gasi numarul permutarilor care admit cel putin o coincidenta .

Acest numar este egal cu

Dar

Pe de alta parte pozitii pot fi alese din multimea celor pozitii in moduri

Deci

Numarul permutarilor de obiecte fara coincidente se obtine acum scazind din numarul tuturor permutarilor care este egal cu numarul permutarilor care admit macar o coincidenta .

Deci .

6.

Bibliografie

1.Dumitru Busneag , Jian Maftei Teme pentru cercurile si concursurile de matematica ale eleviilor , Suisul Romanesc , Craiova 1983

2.T.Albu , I. Ionescu Principiul includerii si al excluderii (G.M nr.6 1969)

3. Seria Gazeta Matematica.

7.

Rezumat

Primcipiul includerii si al excluderii este o tema deosebit de utila in rezolvarea unor probleme 

de divizibilitate, de teoria multimilor , de geometrie si altele .

La inceputul materialului am enuntat teorema generalizata pentru n multimi finite 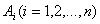demonstrand apoi acest rezultat .

Cu ajutorul acestui principiu am prezentat doua aplicatii in care am demonstrat ca sunt , de exemplu ,734 de numere naturale mai mici sau egale cu 1000 ,divizibile sau cu 2 , sau cu 3 sau cu 5 , teorema aplicandu se pentru trei multimi finite , urmand ca in cea de a doua aplicatie sa determinam numarul de functii surjective , cu

Lucrarea prezinta si alte probleme interesante de la concursuri matematice sau propuse pentru acestea ,abordand si alte teme ca de exemplu : daca avem n puncte in plan care se unesc intre ele prin segmente , si daca nu exista niciun triunghi cu varfurile in cele n puncte , atunci exista cel putin un punct care este extremitatea a cel mult segmente .