Serii Taylor
Fie functia ![]() si
si
![]() , oarecare, dar fixat. Presupunem ca functia
, oarecare, dar fixat. Presupunem ca functia ![]() este indefinit
derivabila intr-o vecinatate
este indefinit
derivabila intr-o vecinatate ![]() (functia
(functia ![]() admite derivate de 737d35h
orice ordin intr-o vecinatatea a
punctului
admite derivate de 737d35h
orice ordin intr-o vecinatatea a
punctului ![]() ). Atunci putem scrie formal seria
). Atunci putem scrie formal seria ![]() in punctul
in punctul ![]()
![]() ,
, ![]() . (1)
. (1)
sau seria de puteri a lui ![]() dupa puterile lui
dupa puterile lui
![]() . Pentru valori fixate ale lui
. Pentru valori fixate ale lui ![]() si
si ![]() seria poate fi
convergenta sau divergenta In cazul cand
seria
seria poate fi
convergenta sau divergenta In cazul cand
seria ![]() este convergenta
atunci suma seriei este egala cu
este convergenta
atunci suma seriei este egala cu ![]() .
.
Seria Taylor este
convergenta catre functia ![]() daca si
numai daca restul formulei lui
daca si
numai daca restul formulei lui
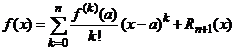 ,
, ![]() (2)
(2)
tinde la zero cand ![]() . Altfel spus, daca
. Altfel spus, daca ![]() atunci, sirul sumelor
partiale
atunci, sirul sumelor
partiale
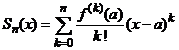 (3)
(3)
converge catre ![]() pentru orice
pentru orice![]() si reciproc.
si reciproc.
In acest caz vom spune ca seria Taylor este convergenta avand suma ![]() si vom scrie
si vom scrie
![]() . (4)
. (4)
Toate functiile analizate in exemplele ![]() sunt dezvoltabile in
serie
sunt dezvoltabile in
serie ![]() (dezvoltabile in serie
in jurul punctului
(dezvoltabile in serie
in jurul punctului ![]() ) si avem
) si avem
![]() . (5)
. (5)
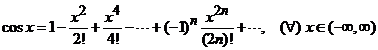 . (6)
. (6)
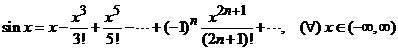 . (7)
. (7)
![]() . (8)
. (8)
![]() , (9)
, (9)
unde ![]() .
.
|