ACŢIONĂRI ELECTRICE
Definitie, structura SAE
Un SAE reprezinta un sistem de conversie a energiei electrice în energie mecanica care asigura controlul pe calea electrica a energiei mecanice obtinute si a parametrilor sai.
Se disting 3 structuri de baza:
I. elementare sau clasice;
II. automatizate;
III. complex automatizate.
(def. sistemului prin sistem se întelege un ansamblu de elemente fizice interconectate, servind unui scop functional comun si în care fenomenele ce se petrec respecta principiul cauzalitatii)
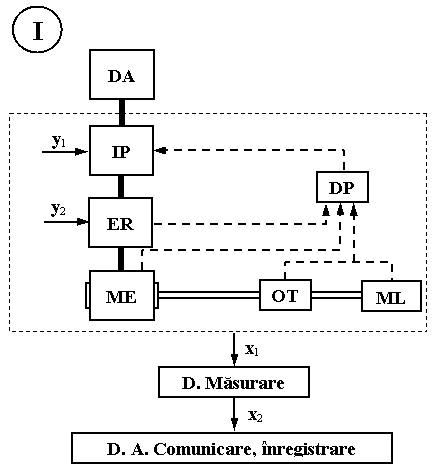 DA
- dispozitiv de alimentare cu energie electrica
DA
- dispozitiv de alimentare cu energie electrica
IP - întrerupator de putere
ER - element de reglare
MR - Motor electric
OT (TM) - organ de transmisie (transmisie mecanica)
ML - mas. de lucru
DP - dispozitiv de protectie
y , y - marimi de comanda
x , x - marimi de masurat, afisat ...
actionarile electrice individuale fara pretentii deosebite cu privire la pornire, reglarea turatiei si frânarea MEA.
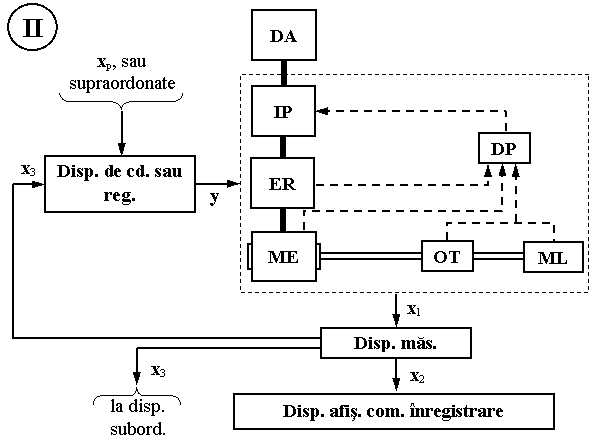
x , x , x - marimi masurate
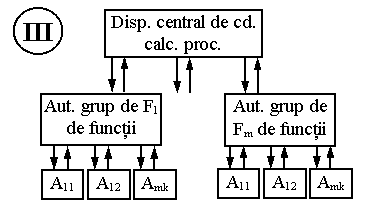 o
unitate de prelucrare a informatiei
algoritm de comanda sau reglare
o
unitate de prelucrare a informatiei
algoritm de comanda sau reglare
D k - S.A.E. II
F ...Fm - automatica grupului de functii
mP.
S.A.E.
 - alegerea
motorului el. cu com.
- alegerea
motorului el. cu com.
- determ. puterii
- verificarea
- stabilirea vitezei
- stabilirea iopt.
- stabilirea sistemelor optime de frânare
- stabilirea metodelor celor mai potrivite de reglare a vitezei
- stabilirea schemei de comanda a SAE
- C. m a ML se întelege Mr (util si de frecari) f(r, a, x....)
Prin regim de funct. a ML se întelege modul de variatie în timp a lui Mr
C. m. si r de functionare ale MEA.
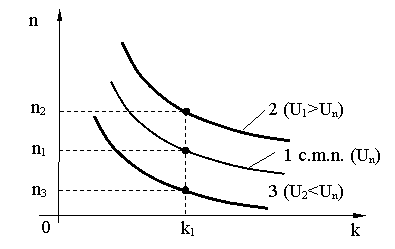
Prin c. m. a MEA n = f(M)
C. m. clasificate: - dupa parametrii electrici ai motorului;
- dupa modul de variatie a turatiei mot. functie de cuplul de pe arborele sau
- c. m. naturala
- c. m. artificiala
Dupa modul de variatie a vitezei: - suprarigide sau sincron
rigide
semirigide (semimoi)
moi
gradul de rigiditate: 
d suprarigide
d rigide
10 < d semirigide
d > 20% moi
Orice MEA motor sau generator
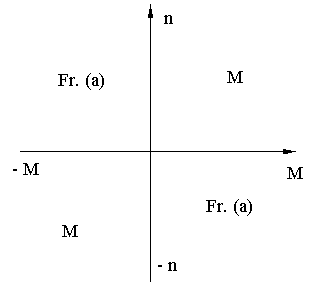
Fr.:
fr. reostatica (dinamica);
fr. c. i. sau contra curent;
fr. cu recuperare de energie.
C. M. si R. F. ale M. E. de c.c. cu excitatie derivatie
C. M. naturala
 U = E + IRa
U = E + IRa
unde:
E t.c.e.m. în indusul motorului
Ra rezistenta proprie a circ. ind. mot.
I curentul de sarcina a motorului
![]()
unde ke si Ce constante ale motorului
p - nr. de perechi de poli
a - nr. de perechi de cai de curent
N - nr. de conductoare active ale indusului mot.
f - flux ct.
![]() sau
sau 
Ţinând cont ca:
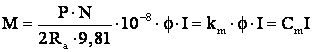
rezulta,
în final 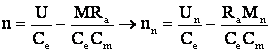 c.m. naturala
c.m. naturala
Obs.: în SI flux Wb (weberi), iar în
MkfSA Mx (maxwell)
dar: ![]() si,
si,
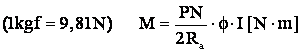
pt.
M = 0 (si frecari, si util) 
n - viteza de mers în gol ideal
Pt.
n = 0 - la pornire: 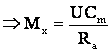
Mp - cuplul de pornire al mot. pe c.m.n.
![]() (mare)
(mare)

n = f(M) - dependenta liniara c.m.n. dreapta
Trasarea expr. c.m. din datele nominale

2 pct. ![]() si
si ![]()
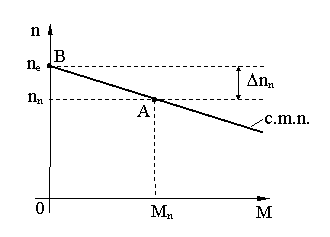 Pt.
Pt.
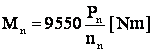
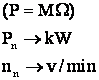
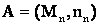
Pt.
B M = 0
si 
din datele nominale:

Revenind la expr. c.m.n.
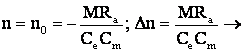 caderea de
viteza
M
caderea de
viteza
M
![]()
 Obs.:
Obs.:
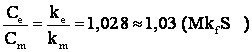
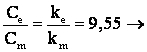 si
si
C.M. artificiala
Din
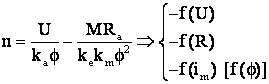
. C.m.a. f(U)
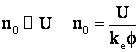
Apar doua aspecte: - separata
- derivatie
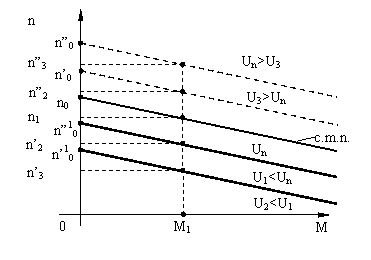 (
~ ) la excit. separata U modifica direct proportional "n
(
~ ) la excit. separata U modifica direct proportional "n
în cazul excit. derivatie U alim. influenteaza atât "n " la numarator cât si f la numitor
la excit. derivatie:
U
![]() n
n
![]() ; iex
; iex
![]() dar nu
influenteaza f
(curba de magnetizare)
dar nu
influenteaza f
(curba de magnetizare)

daca U ![]()
![]() n , iar iex
n , iar iex ![]() f
f![]() c.m. artificiale mai moi la U
c.m. artificiale mai moi la U ![]() fata de cele
de la excit. sep.
fata de cele
de la excit. sep.
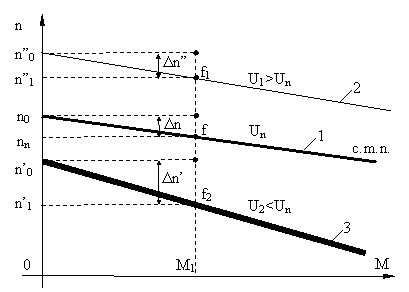
![]()
C.m.a. f(R)
R
Dn - familii de caracteristici care trec toate
prin n
si panta din ce în ce mai cazatoare cu ![]() lui R
lui R
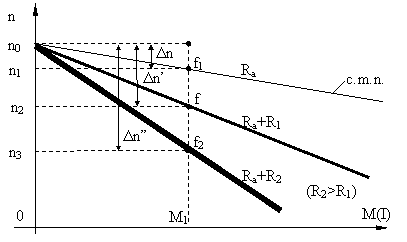
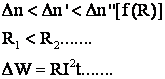
3. C.m.a. obtinute prin modificarea fluxului inductor.
Din
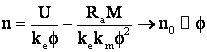
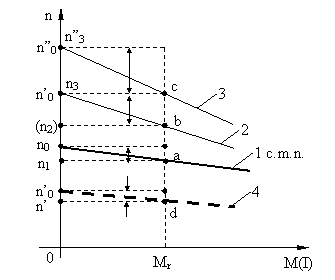
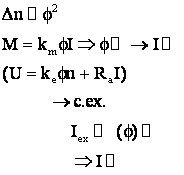
REGIMURILE DE FRÂNARE ALE MEA DE c.c. CU EXCITAŢIE DERIVAŢIE (SEPARATĂ)
regimul de frânare cu recuperare;
regimul de frânare dinamica (reostatica);
regimul de frânare prin c. i. (cu contracurent).
Regimul de frânare cu recuperare.
Pt.
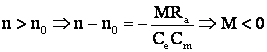 deci cuplu de frânare.
deci cuplu de frânare.
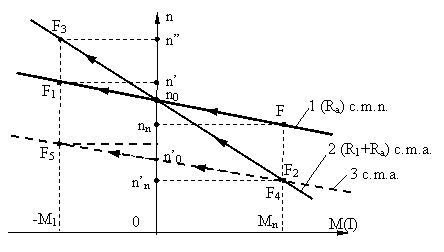
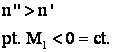
la U'<Ual "3" c.m.a.
Regimul de frânare dinamica
 Din expr. analitica
Din expr. analitica
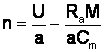
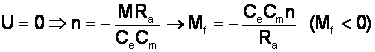
![]()

![]()
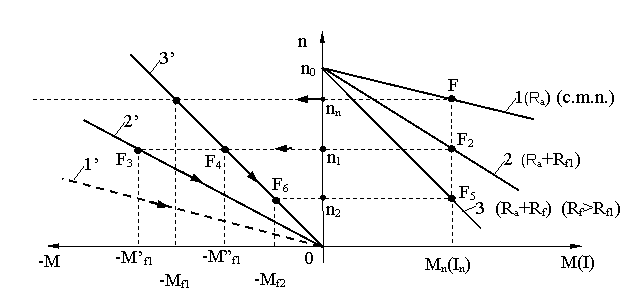
![]()
Cu
cât ![]() cu atât
cu atât ![]() .
.
Regimul de frânare prin c.i.
cu inv. polaritatii tens. de alimentare;
fara inv.
polaritatii tens. de alimentare si introducerea în circ. rotoric
a unei ![]() (suficient de mari).
(suficient de mari).
a) fara inv. polaritatii
![]()
 Din:
Din:

pentru n < 0 (n')
este necesar ca
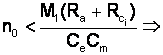
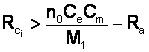
Din:
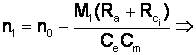
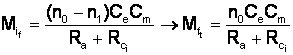
pt. n = 0
Iar:
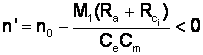 (am pus
conditia )
(am pus
conditia )
b) fr. prin c.i. prin inv. polaritatii
Expresia
analitica devine: 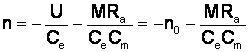 .
.
Deci
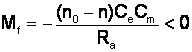 dar
dar 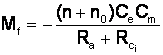

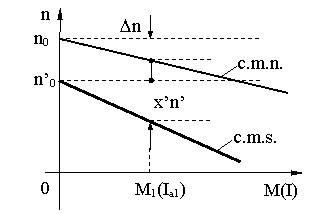
C. m. speciale ale m. d. de c.c. obt. prin suntarea ind.
- rigiditate buna si la viteze mici
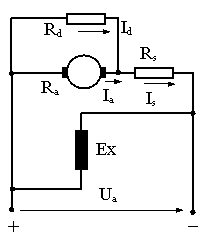
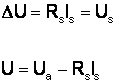
Id - independent de sarcina motorului
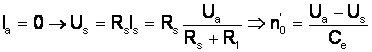
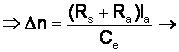 caract. mec. de
rigiditate < decât c.m.n.
caract. mec. de
rigiditate < decât c.m.n.
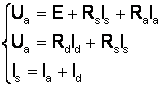
Din Kirchhoff:
Ex. = ct. E = Cen. Pt. expr. c.m.s., n = f(Ia vom elimina din ec. de mai sus Ia si Id. In final
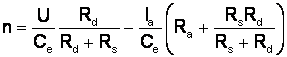 .
.
Notam 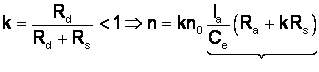
cadere de viteza
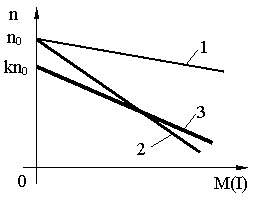
c.m.s. sunt caracterizate prin:
- viteza de mers în gol ideal kn < fata de c.m.n.;
- rigiditate mai mica fata de c.m.n.
însa rigiditatea c.m.s. obt. prin suntarea ind. este mai buna decât a c.m.a f(R)
 Ra Dn
~ Ra
Ra Dn
~ Ra
Ra + Rs Dn ~ Ra + Rs
Ra + kRs Dn ~ Ra + kRs
Pt. o aceeasi încarcare cu cât
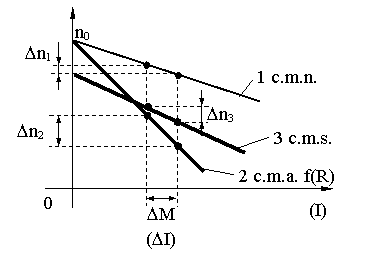
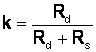 va fi < 1 turatia ideala (la gol) a motorului de
c.c. va fi mai mica, iar rigiditatea c.m.s. va fi mai buna.
va fi < 1 turatia ideala (la gol) a motorului de
c.c. va fi mai mica, iar rigiditatea c.m.s. va fi mai buna.
![]() stabilitate buna pe 1, 3, 2
stabilitate buna pe 1, 3, 2
s-a mentionat ca atât viteza de mers în gol, cât si rigiditatea c.m.s. depind de valoarea lui "k" pt. diverse valori ale lui Rs si Rd c.m.s. de pante si viteze de mers în gol ideal definite.
vom analiza pe rând influenta lui Rs si Rd familii de caracteristici m. s. obt prin suntarea ind.
Din examinarea relatiei:
2 familii de c.m.s. 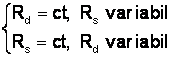
Astfel, pentru Rd = ct. si dând diferite valori rezistentei Rs o familie de c.m.s. concurente într-un singur punct.

pt. Rs c.m.n. punct de intersectie a familiilor de c.m.s. se va gasi pe c.m.n.
intersectând c.m.n.:
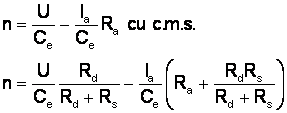
în
care Rs
= ct. si Rs
variabil
coordonatele punctului de intersectie
"Ai" 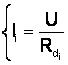 si
si 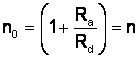 oricare ar fi Rs pct. de intersectie ramâne
neschimbat, deoarece coordonatele lui "Ai" va depinde de "Rs". La limita pentru
Rs
c.m.s. trece prin "0" si "Ai
oricare ar fi Rs pct. de intersectie ramâne
neschimbat, deoarece coordonatele lui "Ai" va depinde de "Rs". La limita pentru
Rs
c.m.s. trece prin "0" si "Ai
c.m.s. pt. Rs = variabil si Rd = ct. sunt cuprinse
între cele 2 limite: Rs
= 0 si
Rs
pt. un alt Rd un alt punct "Ai". Cu cât Rd este mai mare rigiditatea mai mica.
Pt. Rs = ct. si Rd = varibil, la limita, când Rd = 0 expresia c.m.s. devine:
c.m. cu c.m.n. si care trece prin origine.
- Pt. Rs = ct. si Rd variabil, coordonatele acestui punct rezulta din rezolvarea sistemului de ecuatii format din: (ec. anterioara)
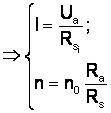
nu depind de Rd deci oricare ar fi valoarea lui Rd, punctul de intersectie "Bi" ramâne acelasi, dar depinde de valoarea lui Rs. Cu cât Rs >> "Bi" mai apropiat de ordonata, rigiditate <.
Din
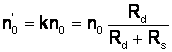 valoarea maxima a acestei viteze nu poate
depasi "U "
pe c.m.n. si tinde spre ea când Rd
familii de c.m.s. între Rd la
c.m.n. prin "0" si Rd , prin
"n " pe
c.m.n. si prin "Bi
valoarea maxima a acestei viteze nu poate
depasi "U "
pe c.m.n. si tinde spre ea când Rd
familii de c.m.s. între Rd la
c.m.n. prin "0" si Rd , prin
"n " pe
c.m.n. si prin "Bi
Cu cât Rs este mai mic "Bi" departe de ordonata si c.m.s. mai rigide.
Variind simultan Rs si Rd o infinitate de caracteristici si deci un reglaj al vitezei motorului.
Gama de reglare comparabil cu cea obtinuta cu R în indus
un reglaj fie de viteza, fie din Rd, fie cu Rs
sensul reglarii vitezei este descrescator;
functionare stabila;
performante energetice <<.
C.M. si R.F. ale motoarelor de c.c. cu excitatie în serie
C.m. naturala

f aI - pe portiunea liniara a caracteristici de magnetizare
(valabil doar pentru M << Mn) pt. M > Mn erori mari
Din:
![]() cu Ra, rezist. totala,
ind. si ex.
cu Ra, rezist. totala,
ind. si ex.
![]() .
.
Dar:
![]() adica
adica 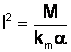 .
.
Deci
 , de unde:
, de unde:
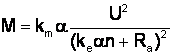 .
.
|
M |
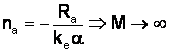
pt. M = 0 n
Din n = 0
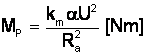
I f. mare.
- productivitate
- autoregulator de viteza
- securitate
I%
n
m
C.M. univ.
din caracteristicile grafice sau tabelar, date nominale ale mot. plus relatia:
 c.m.n.
c.m.n.
imposibila dat. lui a
De
ex.: ![]() si nn = 1000 r/min
si nn = 1000 r/min
Deci pt. c.m.n.: mai întâi din
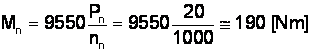
|
I[A] |
|
|
|
|
n[r/min] |
|
|
|
|
M[Nm] |
|
|
|
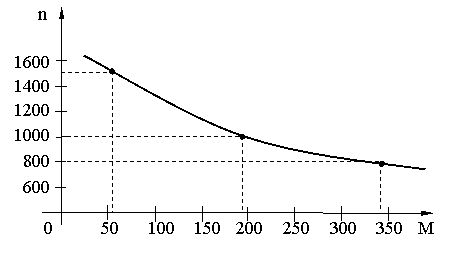 cu
datele de mai sus
c.m.n.
cu
datele de mai sus
c.m.n.
c.m.n. a mot. cu excit. mixta se traseaza de asemenea plecând de la c.m. univ. + date nom.
Caract. mec. limita a mot. de c.c. cu excitatie serie
Din analiza lui "a" din f aI, se defineste c.m. lim. ca fiind c.m. tot. pentru cazul teoretic când Ra = 0, caz fictiv ipotetic, imposibil de realizat.
Din:
![]() cu Ra
cu Ra ![]()
sau
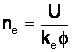 si la fel, cazul
real
si la fel, cazul
real
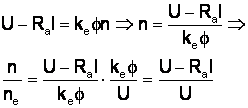
deci: ![]() sau
sau 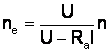 .
.
Din
relatiile ant. 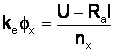 .
.
Din: 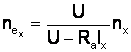 si c.m.n.
si c.m.n.
c.m.l. este situata deasupra c.m.n.
c.m.l. mai apropiata de c.m.n. la sarcini mici
c.m.l. mai departata de c.m.n. pt. cupluri mari
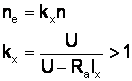

Din
c.m.l. si cu relatia ![]() , se poate trasa c.m.n. si de asemenea c.m.a. obt.
fie prin modificarea tens. de alimentare "U" fie prin introd. unei "Rsupl " în circ. mot.
, se poate trasa c.m.n. si de asemenea c.m.a. obt.
fie prin modificarea tens. de alimentare "U" fie prin introd. unei "Rsupl " în circ. mot.
C.M. ARTIFICIALE
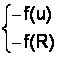 si a f(f
si a f(f
a). C.m.a. obt. f(U)
- pt. Mr = ct. n ~ U
- din ecuatia echilibrului de tensiune
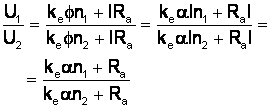
dar Ra << kean
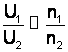
c.m.a. sunt paralele cu c.m.n. situate deasupra sau dedesubtul c.m.n.
 -
trasarea c.m.a. obt prin modificarea tens. de alimentare pot fi trasate
plecând tot de la c.m.l.
-
trasarea c.m.a. obt prin modificarea tens. de alimentare pot fi trasate
plecând tot de la c.m.l.
b) C.m.a. obt. f(R)
- la fel ca la mcc cu excit derivatie, rigiditatea lor cu Rsupl introdusa.
![]()

c) C.m.a. obt. prin modificarea fluxului inductor
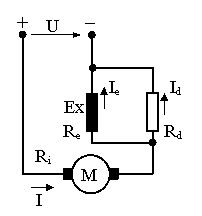
suntarea circuitului inductor
din legile lui Kirchoff:
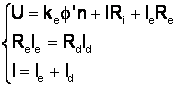 ,
,
unde Ri + Re = Ra
eliminând pe Ie si Id din aceste relatii:
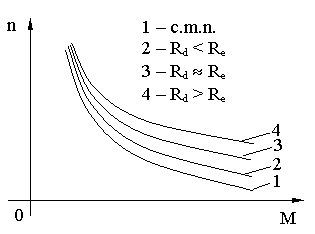
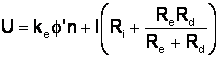
de unde:
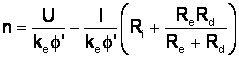
dar
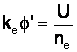

c.m.a. se departeaza de c.m.n. cu cât Rd în comparatie cu Re
Reg. de frânare ale mcc cu excit. serie
nu este posibil obt. reg. de frânare cu recuperare (doar în conditii speciale). Vom discuta:
o reg. de frânare dinamica;
o reg. de frânare prin c.i.
a) Reg. de frânare dinamica
decuplarea motorului de la retea si cuplarea pe Rf
decuplarea ind. si cuplarea pe Rf, ex. ramânând cuplata
din:
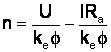 , dar
, dar
f
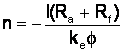
dar
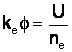
![]()
cu datele anterioare si calculele pt. c.m.l.
n = f(M) la frânare;
cu cât Rf la acelasi cuplu Mf n
n f Mf , deci la viteze mici, Mf
inversarea polaritatii circ. inductor
fr. dinamica putin folosita
este folosita a 2-a metoda
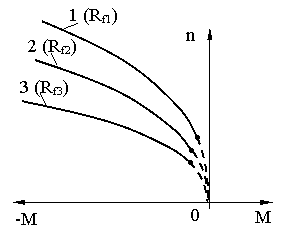
![]()
la f - ct. Mcc cu excitatie derivatie
b) Reg. de frânare prin c.i.
cu introducerea de Rci suficient de mari
a 2-a metoda nu este folosita
pt. oprire:
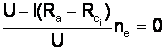
![]()
![]()
pt. I = In
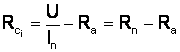
- Rg. de fr. c.i. prin inv. polaritatii nu se foloseste: complicatii nejustificate de avantaje deosebite.
|