![]()
Calculul termic al unui motor cu aprindere prin scinteie.
Pentru exemplificarea metodei se va efectua calculul termic a unui MAS capabil sa furnizeze la turatia n=5400 rot/min o putere nominala Pn=72KW. Motorul are un numar i=4 cilindri.
Alegerea parametrilor initiali. Pe baza recomandarilor existente in literatura de specialitate ti a rezultatelor obtinute pe motoare experimetale se adopta urmatoarele valori:
temperatura initiala: T0=293K;
![]() presiunea initiala: P0=1,02 x 105 N/m2;
presiunea initiala: P0=1,02 x 105 N/m2;
coeficientul de exces de aer: ![]() =0,85;
=0,85;
temperatura gazelor reziduale: Tr= 10002
raportul de comprimare: ![]() =8
=8
Parametrii procesului de schimbare a gazelor. Se adopta
urmatoarele marimi: ![]()
presiunea la sfirsitul admisiei Pa=0,8 x 105 N/m2;
preincalzirea amestecului ![]() T=25 0C
T=25 0C
coeficientul de post umplere vp
Se calculeaza in continuare coeficientul gazelor reziduale:
![]() r =
r =![]()
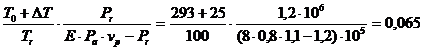
![]()
![]()
Temperatura la sfirsitul admisiei va fi:
![]() K
K![]()
Coeficientul de umplere rezulta:
![]()
Parametri procesului de comprimare. Se adopta pentru coeficientul politropic de comprimare ca valoarea n1=1,34.
Presiunea la sfirsitul comprimarii rezulta:
![]()
Temperatura la sfirsitul comprimarii va fi:
![]() =
=![]()
Parametri procesului de ardere. Conform tabelului 7 se adopta urmatoarea compozitie a benzinei:
c=0,654kg; h=0,142kg; o=0,004kg; si avind puterea calorica inferioara Q1=43500kj/kg.
Se mai adopta conform recomandarilor din tabelul 4:
coeficientul de utilizare a caldurii E=0,9;
masa molara a combustibilului:M0=1/114;
Aerul minim necesar arderii a 1kg de combustibil se calculeaza cu relatia:
Lmin=![]()
Cantitatea de aer necesara arderii:
L=![]()
Cantitatea de incarcatura proaspata, raportata la 1 kg combustibil va fi:
![]()
Coeficientul teoretic de variatie molara a incarcaturii
proaspete pentru![]() <1 este:
<1 este:
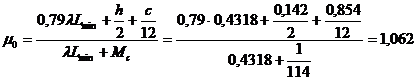
Coeficientul real de variatie molara a incarcaturii proaspete rezulta
![]()
Caldura specifica molara medie a amestecului initial este:
![]()
Caldura specifica molara medie a gazelor de ardere pentru ![]() <1este :
<1este :
![]()
![]()
Caldura specifica degajata de arderea incompleta va fi :
![]()
![]()
Temperatura la sfirsitul arderii rezulta din urmatoarea ecuatie :
![]()
![]()
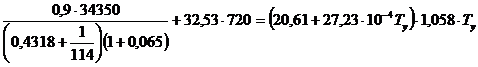
![]()
Presiunea la sfirsitul arderii se calculeaza cu relatia :
![]()
Tinind cont de rotunjirea diagramei:
![]()
Coeficientul ![]() se alege din tabelul 4.
se alege din tabelul 4.
Gradul de crestere a presiunii va fi:
![]()
![]()
Valorile calculate se compara cu cele existente in tabelele 4 si 5.
Destinderea. Se adopta coeficientul politropic al destinderii n2 = 1,25
Presiunea la sfirsitul destinderii rezulta:
![]()
Temperatura la sfirsitul destinderii va fi:
![]()
Valorile calculate trebuie sa se compare cu cele din tabelul 8.
Parametri principali ai motorului. Se adopta urmatoarele valori pentru:
- coeficientul de rotunjire a
diagramei : ![]()
- randamentul mecanic:![]()
Presiunea medie a ciclului teoretic se obtine din relatia:
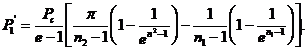
![]()
![]()
Randamentul indicat al motorului este:
![]()
Presiunea medie efectiva rezulta:
![]()
Randamentul efectiv al motorului va fi :
![]()
Consumul specific efectiv de combustibil se calculeaza cu relatia:
![]() ui.
ui.
Dimensiuni
fundamentale ale motorului. Se adopta raportul cursa- alezaj:
![]()
Capacitatea cilindrica necesara va fi :
![]()
![]()
![]()
Se determina alezajul si cursa:
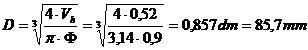
![]()
Viteza medie a pistonului este :
![]()
Cilindreeia totala a motorului rezulta :
![]()
Puterea litrica a motorului rezulta:
![]()
Capitolul 2
Caracteristica externa
|
Puterea nominala |
|
72 |
|
|
|
Turatia nominala |
|
5400 |
|
|
|
Coef. de adaptabilitate |
1,3 |
|
||
|
Coef. de elasticitate |
|
0,5 |
|
|
|
Coeficientii puterii |
ß1 |
1 |
|
|
|
|
|
ß2 |
1,2 |
|
|
|
|
ß3 |
-1,2 |
|
|
Consum specific la reg. nom. |
250 |
|
||
|
Coef. consum specific |
a1 |
1,55 |
|
|
|
|
|
a2 |
-1,55 |
|
|
|
|
a3 |
1 |
|
|
Turatia minima |
|
800 |
|
|
|
Turatia maxima |
|
5940 |
|
|
|
|
|
|
|
|
|
n |
Pe |
Me*10 |
ce |
C |
|
rot/min |
kW |
Nm |
g/kWh |
kg/h |
|
800 |
12,28 |
1466,17 |
335,58 |
4,12 |
|
1000 |
15,75 |
1503,90 |
324,31 |
5,11 |
|
1200 |
19,32 |
1537,43 |
313,73 |
6,06 |
|
1400 |
22,97 |
1566,78 |
303,84 |
6,98 |
|
1600 |
26,67 |
1591,93 |
294,63 |
7,86 |
|
1800 |
30,40 |
1612,89 |
286,11 |
8,70 |
|
2000 |
34,13 |
1629,66 |
278,28 |
9,50 |
|
2200 |
37,83 |
1642,23 |
271,12 |
10,26 |
|
2400 |
41,48 |
1650,62 |
264,66 |
10,98 |
|
2600 |
45,05 |
1654,81 |
258,88 |
11,66 |
|
2800 |
48,52 |
1654,81 |
253,79 |
12,31 |
|
3000 |
51,85 |
1650,62 |
249,38 |
12,93 |
|
3200 |
55,03 |
1642,23 |
245,66 |
13,52 |
|
3400 |
58,02 |
1629,66 |
242,63 |
14,08 |
|
3600 |
60,80 |
1612,89 |
240,28 |
14,61 |
|
3800 |
63,34 |
1591,93 |
238,61 |
15,11 |
|
4000 |
65,62 |
1566,78 |
237,64 |
15,59 |
|
4200 |
67,61 |
1537,43 |
237,35 |
16,05 |
|
4400 |
69,29 |
1503,90 |
237,74 |
16,47 |
|
4600 |
70,62 |
1466,17 |
238,82 |
16,87 |
|
4800 |
71,59 |
1424,25 |
240,59 |
17,22 |
|
5000 |
72,15 |
1378,13 |
243,04 |
17,54 |
|
5200 |
72,30 |
1327,83 |
246,18 |
17,80 |
|
5400 |
72,00 |
1273,33 |
250,00 |
18,00 |
|
5500 |
71,67 |
1244,51 |
252,17 |
18,07 |
|
5700 |
70,65 |
1183,73 |
257,02 |
18,16 |
|
5900 |
69,12 |
1118,75 |
262,56 |
18,15 |
|
|
|
|
|
|
In figura 3.1. este prezentata schema mecanismului biela manivela axat, unde s-au facut urmatoarele notatii:
- unghiul de rotatie a arborelui cotit, se masoara in sensul de rotatie a arborelui cotit;
![]() - viteza unghiulara de
rotatie a arborelui cotit, in s-1;
- viteza unghiulara de
rotatie a arborelui cotit, in s-1;
n - turatia arborelui cotit, in rot/min;
R - raza manivelei (distanta dintre axa arborelui cotit si axa fusului maneton), in m;
S = 2R - cursa pistonului (distanta dintre p.m.s. si p.m.i.) in m;
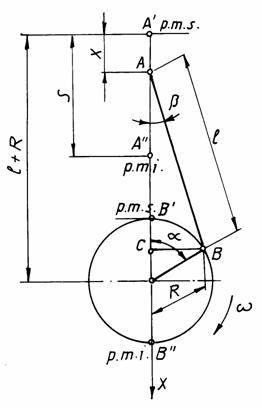
l -
lungimea bielei, in [m].
Se defineste raportul =R/l - raportul dintre raza manivelei si lungimea bielei;
Pentru motoare de autovehicule = l/3,2…l/4,2.
Deplasarea pistonului. Legea de variatie a deplasarii pistonului in functie de unghiul s-a determinat pe cale analitica:
![]() (3.1)
(3.1)
Viteza pistonului. Derivand relatia (3.1) in raport cu timpul se obtine expresia analitica a vitezei pistonului:
![]() (3.3)
(3.3)
Acceleratia pistonului. Derivand in raport cu timpul expresia vitezei pistonului (3.3) se obtine:
![]()
|
|
|
|
|
|
raza manivelei[mm] |
|
40,58816 |
|
|
b=r/l |
|
|
0,277778 |
|
viteza unghiulara |
|
565,4867 |
|
|
|
|
|
|
|
|
xp |
vp |
ap |
|
[°RAC] |
[mm] |
[m/s] |
[m/s^2] |
|
0 |
0,00 |
0,00 |
16584,39 |
|
10 |
0,79 |
5,08 |
16169,78 |
|
20 |
3,11 |
9,90 |
14958,17 |
|
30 |
6,85 |
14,24 |
13042,87 |
|
40 |
11,82 |
17,89 |
10568,61 |
|
50 |
17,81 |
20,72 |
7716,74 |
|
60 |
24,52 |
22,64 |
4686,89 |
|
70 |
31,68 |
23,62 |
1677,29 |
|
80 |
39,01 |
23,69 |
-1134,08 |
|
90 |
46,23 |
22,95 |
-3605,30 |
|
100 |
53,10 |
21,51 |
-5641,67 |
|
110 |
59,45 |
19,52 |
-7200,93 |
|
120 |
65,11 |
17,12 |
-8292,19 |
|
130 |
69,99 |
14,44 |
-8968,85 |
|
140 |
74,01 |
11,61 |
-9316,50 |
|
150 |
77,15 |
8,72 |
-9437,57 |
|
160 |
79,39 |
5,80 |
-9434,53 |
|
170 |
80,73 |
2,90 |
-9394,03 |
|
180 |
81,18 |
0,00 |
-9373,78 |
|
190 |
80,73 |
-2,90 |
-9394,03 |
|
200 |
79,39 |
-5,80 |
-9434,53 |
|
210 |
77,15 |
-8,72 |
-9437,57 |
|
220 |
74,01 |
-11,61 |
-9316,50 |
|
230 |
69,99 |
-14,44 |
-8968,85 |
|
240 |
65,11 |
-17,12 |
-8292,19 |
|
250 |
59,45 |
-19,52 |
-7200,93 |
|
260 |
53,10 |
-21,51 |
-5641,67 |
|
270 |
46,23 |
-22,95 |
-3605,30 |
|
280 |
39,01 |
-23,69 |
-1134,08 |
|
290 |
31,68 |
-23,62 |
1677,29 |
|
300 |
24,52 |
-22,64 |
4686,89 |
|
310 |
17,81 |
-20,72 |
7716,74 |
|
320 |
11,82 |
-17,89 |
10568,61 |
|
330 |
6,85 |
-14,24 |
13042,87 |
|
340 |
3,11 |
-9,90 |
14958,17 |
|
350 |
0,79 |
-5,08 |
16169,78 |
|
360 |
0,00 |
0,00 |
16584,39 |
Prin calculul dinamic al mecanismului biela-manivela se urmareste determinarea marimii si caracterului variatiei sarcinilor care actioneaza asupra pieselor motorului. Cercetarile in detaliu sunt foarte complexe din cauza regimului variabil de functionare. De aceea se folosesc relatii simplificate, obtinute in ipoteza unei viteze unghiulare constante a arborelui cotit si la regim stabilizat.
Asupra mecanismului biela-manivela, actioneaza fortele date de presiunea gazelor din cilindru si fortele de inertie ale maselor mecanismului aflate in miscare. Fortele de frecare vor fi considerate neglijabile. Fortele de inertie sunt constituite din fortele de inertie ale maselor aflate in miscare alternativa de translatie (indice j) si forte de inertie ale maselor aflate in miscare de rotatie (indice r).
Pentru calculul organelor mecanismului biela-manivela, al sarcinilor in lagare, pentru cercetarea oscilatiilor de torsiune, etc., trebuie determinate valorile maxime, minime si medii ale acestor forte. De aceea marimile fortelor se vor determina pentru o serie de pozitii succesive ale mecanismului, functie de unghiul de rotatie al arborelui cotit.
Forta data de presiunea gazelor pe piston se determina cu relatia:
![]() (4.1.)
(4.1.)
in care:
pg - presiunea de lucru sau suprapresiunea, in [N/m2];
pind - presiunea indicata in cilindru dupa diagrama indicata in [N/m2];
po - presiunea mediului ambiant(po=105[N/m2];
![]() - aria capului
pistonului, in [m2];
- aria capului
pistonului, in [m2];
D - diametrul pistonului, in [m].
Variatia presiunii indicate a gazelor din cilindru in functie de unghiul de rotatie a arborelui cotit s-a determinat la calculul termic, prin trasarea diagramei indicate desfasurate (cronomanogramei).
Forta de presiune a gazelor este indreptata dupa axa cilindrului si poate fi considerata in axa boltului de piston. Aceasta forta este considerata pozitiva cand este orientata spre axa arborelui cotit (pind > po) si negativa cand este orientata invers (pind < po).
Calculul valorilor fortei de presiune a gazelor se face tabelar. Se construieste curba Fg = f().
Fortele de inertie sunt produse de masele aflate in miscare accelerata si anume: piston asamblat (piston, bolt, segmenti, sigurantele boltului), biela si arbore cotit.
Aceste forte sunt produse de masele pistonului asamblat (piston, segmenti, bolt de biela si sigurantele acestuia) si o parte din masa bielei si sunt considerate concentrate in axa boltului.
Determinarea fortelor de inertie ale maselor aflate in miscare de translatie se face cu relatia:
![]() (4.2)
(4.2)
unde: mj - masele pieselor in miscare de translatie, in [kg];
ap- acceleratia pistonului, in [m/s2].
Masele aflate in miscare de translatie se determina cu relatia urmatoare:
![]() (4.3)
(4.3)
unde: mp - masa pistonului asamblat, in [kg];
m1b - masa bielei concentrata in axa boltului si care se considera ca executa miscare de translatie, in [kg].
Fortele de inertie Fj se pot exprima, tinand seama de expresia acceleratiei pistonului pentru mecanismul biela-manivela axat:
![]() (4.4)
(4.4)
Calculul valorilor fortelor Fj se face tabelar si se construieste curba Fj = f().
Aceste forte sunt produse de o parte din masa bilei si masa neechilibrata a unui cot al arborelui cotit (masa manetonului si masele reduse ale celor doua brate).
Fortele de inertie ale maselor in miscare de rotatie se determina cu relatiile:
![]() forta centrifuga (4.5)
forta centrifuga (4.5)
unde: mr - masa in miscare de rotatie, in [kg];
R - raza manivelei, in [m];
- viteza unghiulara a arborelui.
In consecinta, fortele de inertie ale maselor in miscare de rotatie sunt fortele centrifuge ce actioneaza pe directia razei manivelei si raman constante ca marime.
Recomandari privind determinarea maselor in miscare de rotatie se prezinta in paragraful 4.1.2.3.
Pentru simplificarea calculelor, masele pieselor in miscare pot fi inlocuite cu mase reduse concentrate in articulaliile mecanismului biela-manivela.
Masa bielei este considerata ca fiind concentrata in cele doua axe in care este articulata, respectiv in axa ochiului bielei (m1b) si in axa capului bielei (m2b).
Componenta m1b a masei bilei se considera ca executa miscare de translatie si este luata in calculul fortei de inertie Fj. A doua componenta m2b se adauga maselor rotitoare ale mecanismului.
Pentru majoritatea motoarelor de autovehicule, repartizarea masei bielei pe cele doua componente este:
![]() (4.6)
(4.6)
![]()
sau, cu suficienta aproximatie:
![]() (4.7)
(4.7)
![]()
In aceste conditii, masa elementelor aflate in miscare de translatie alternativa se poate determina cu relatia:
![]() (4.8)
(4.8)
unde: mp - masa pistonului asamblat, in [kg];
mb - masa bielei , in [kg].
Masele rotitoare mr, sunt constituite din masa fusului maneton mm, masa bratului de manivela redusa la raza R a manivelei si componenta m2b a bielei, adica:
![]()
Masa bratelor manivelei avand centrul de masa la raza r fata de axa arborelui cotit, se poate reduce la raza R a manivelei pornind de la egalitatea:
![]()
de unde se obtine:
![]() (4.9)
(4.9)
unde reprezinta distanta de la axa arborelui cotit la centrul de greutate al bratului.
In cazul existentei unor contragreutati pe bratele manivelei, trebuie sa se tina seama de masa acestora reducand-o la raza R si scazand-o din masa bratelor manivelei.
Prin insumarea algebrica a fortelor de presiune a gazelor Fg si fortelor de inertie Fj, determinate pentru diferite pozitii ale manivelei, se obtin valorile fortei sumare care actioneaza in lungul axei cilindrului.
![]() (4.10)
(4.10)
Calculul valorilor fortei F se face tabelar si se construieste curba F=f().
|
Fig.4.1. Fig.4.2. Fortele care actioneaza Sensurile fortelor care in motorul monocilindric actioneaza in motor |
In figura 4.1. se prezinta schema de descompunere a fortelor sumare F, iar in fig.4.2. sensurile pozitive, respectiv negative ale fortelor.
Forta F aplicata in axa boltului se descompune in doua componente, una de sprijin, normala pe axa cilindrului (N) si una dupa axa bielei (B):
![]() (4.11)
(4.11)
![]() (4.12)
(4.12)
Calculul fortelor N si B se face tabelar si se reprezinta grafic curbele N=f() si B=f().
In axa fusului maneton, forta B se descompune in doua componente, una radiala (Z) si una tangentiala (T), expresiile lor fiind urmatoarele:
![]() (4.13)
(4.13)
![]() (4.14)
(4.14)
Pe baza calculului tabelar al valorilor fortelor T si Z se traseaza curbele T=f() si Z=f().
Forta tangentiala T este singura forta care produce momentul motor. Expresia momentului motor este:
![]() (4.18)
(4.18)
Raza manivelei R, in [m], fiind constanta, curba de variatie a momentului motor functie de unghiul de rotatie al manivelei este identica cu cea a fortei tangentiale T, evident la o scara adecvata.
Momentul motor total se obtine prin insumarea momentelor obtinute pentru fiecare cilindru al motorului tinand cont de ordinea de functionare a acestora si de configuratia arborelui cotit. De asemenea, se poate obtine suma momentelor ce actioneaza asupra fiecarui fus palier al arborelui cotit.
Se stabileste variatia momentului motor total functie de unghiul de rotatie a arborelui cotit, precum si valoarea momentului mediu. Cu valoarea momentului mediu se calculeaza puterea dezvoltata de motor care se compara cu puterea obtinuta la calculul termic.
Ca pozitie de pornire (=0) se considera pozitia corespunzatoare p.m.s. a primului cilindru, aflat la admisie.
Pentru motorul de fata, cu 4 cilindri in linie, se considera ordinea de functionare a cilindrilor 1 - 3 – 4 – 2 – 1. Unghiul dintre manivele si dintre doua aprinderi succesive este de 180 °RAC.
|