Electromagnetismul

Electromagnetismul

d)      Cea de-a patra ecuatie Maxwell se numeste "legea lui Ampčre completata de Maxwell". Sub forma integrala ea este:

unde este intensitatea curentului (fluxul vectorului densitate de curent) iar fluxul câmpului electric printr-o suprafata (deschisa) sprijinita pe conturul indus . Aceasta lege semnifica faptul ca se poate produce un câmp magnetic cu linii de câmp închise cu ajutorul unui curent electric sau/si cu ajutorul unui câmp electric variabil în timp. Termenul a fost numit

curent de deplasare (prin analogie cu un dielectric plasat într-un crescator, ale carui unde se deformeaza continuu, sarcinile lor formând un curent de deplasare) si legea se poate scrie:

Daca transformam circulatia lui de-a lungul conturului închis în integrala de suprafata (teorema lui Stokes):

se obtine legea lui Ampčre completata de Maxwell sub forma diferentiala:

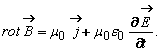
Acestor patru ecuatii li se adauga legile de material:

1) unde este vectorul de deplasare sau inductia câmpului electric, este polarizatia, este susceptibilitatea electrica, este permitivitatea electrica absoluta a mediului. În medii omogene, liniare si izotope (nefero-electrice) si sunt marimi scalare.

2) unde este vectorul intensitate a câmpului magnetic, este magnetiztia, este susceptibilitatea magnetica a mediului, este permeabilitatea magnetica relativa a mediului iar este permeabilitatea magnetica absoluta a mediului. În medii omogene liniare si izotrope, (nefero-magnetice) si sunt marimi scalare.

3) Legea fortei: exprima forta exercitata asupra unui purtator de sarcina în câmpuri electrice si magnetice.

4) unde este densitatea de curent iar este conductivitatea mediului, reprezinta legea lui Ohm sub forma locala.

Ecuatiile lui Maxwell împreuna cu relatiile de material în mediile liniare si izotope nu determina uniunea decât daca, alaturi de conditiile initiale se cunosc conditiile de la frontiera domeniului considerat.

Conditii la limita:

Consideram suprafata continua de separatie între doua medii liniare si izotope, notate 1 si 2, normala la elementul de arie, fiind orientata conventional de la mediul 1 spre mediul 2. La aceasta suprafata, câmpurile sufera o discontinuitate, descrisa de conditiile la limita sau ecuatiile de trecere. Se considera o suprafata închisa de forma cilindrica cu "capacele" infinitezimale, de arie , paralele cu suprafata de separatie si situate unul în mediul 1 si celalalt în mediul 2.

a)      Fluxul lui prin cutie trebuie sa fie nul. Deoarece fluxul prin aria laterala este neglijabil, ramâne fluxul prin cele doua "capace": unde sunt câmpurile magnetice din cele doua medii, în vecinatatea suprafetei. Ultima ecuatie exprima faptul ca adica egalitatea componentelor normale la suprafata, ale câmpului magnetic.

Un rationament asemanator se poate aplica vectorului deplasare sau inductiei electrice Plecam de la legea lui Gauss pentru câmpul electric:

Sarcina din interiorul cilindrului este:

unde este înaltimea cilindrului. Când tindem cu cilindrul se reduce la elementul de arie si sarcina devine o sarcina superficiala caracterizata de densitatea superficiala:

astfel obtinem:

legea lui Gauss devine:

Neglijând fluxul prin aria laterala a cilindrului obtinem:

Deoarece relatia devine:

unde este o eventuala sarcina superficiala libera localizata pe suprafata. Componenta normala a deplasarii electrice se conserva daca si prezinta o discontinuitate când

Pentru celelalte doua ecuatii ale lui Maxwell vom considera un contur dreptunghiular având doua laturi paralele cu suprafata, una în mediul 1 si cealalta în mediul al 2-lea. Ele au lungimi egale si au ca versor vectorul . Laturile perpendiculare pe suprafata sunt infinitezimale în comparatie cu

Circulatia câmpului electric de-a lungul acestui contur va fi:

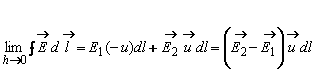
Cantitatea 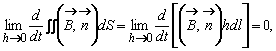este nula deoarece 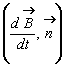pastreaza o valoare finita pentru . Altfel spus, chiar daca este discontinuu, câmpul magnetic este finit în vecinatatea suprafetei de discontinuitate si atunci fluxul derivatei sale temporale printr-o arie care tinde la zero este nul. Obtine:

unde este tangenta la suprafata de separatie. Rezulta continuitatea componentei tangentiale a câmpului electric:

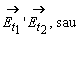
Legea lui Ampčre completata de Maxwell:

se trateaza într-un mod asemanator. fiind o marime finita, chiar daca sufera o discontinuitate, fluxul prin aria care tinde la zero a conturului dreptunghiular este zero. Curentul de conductie al sarcinilor libere poate fi diferit de zero, daca avem un curent superficial. Fluxul sau este: unde este versorul normalei la suprafata dreptunghiulara a conturului, tangenta la suprafata de discontinuitate, este densitatea de curent superficial. Obtinem:

Grupând cele patru conditii la limita:

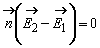
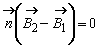
unde este orientat de la mediul 1 catre mediul 2, ele ne indica modul în care se schimba, sau nu, componentele vectorului care caracterizeaza câmpul electromagnetic, la trecerea prin suprafata de discontinuitate.

6) Câmpul electric în substanta

6.1 Introducere

Daca plasam un atom în câmp electric exterior, asupra nucleului încarcat pozitiv se va exercita forta iar asupra norului electronic se va exercita o forta de sens contrar . Putem considera un nor electronic având densitatea volumica

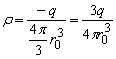
În acord cu teorema lui gauss putem afla intensitatea câmpului electric în interiorul norului electronic uniform încarcat:

unde este distanta de la centrul norului electronic. Daca în prezenta unui câmp exterior nucleul si centrul norului electronic sunt separati prin distanta , asupra nucleului se exercita din partea norului o forta egala cu:

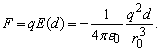
Aceasta forta trebuie sa fie compensata de catre câmpul electric exterior pentru ca nucleul sa fie în echilibru: 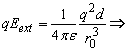distanta de echilibru este:

Astfel, câmpul electric exterior a transformat atomul într-un dipol electric al carui moment dipolar este:

proportional cu câmpul aplicat. Constanta de proportionalitate se numeste polarizabilitatea atomica:

.

În afara de a polariza atomii unei substante, câmpul electric exterior poate alinia moleculele, cum ar fi cele de apa, care poseda deja un moment electric dipolar.

În absenta câmpului extern, aceste molecule sunt orientate, datorita agitatiei termice, haotic si suma momentelor electrice dipolare din unitatea de volum, polarizatia este nula. Aplicând un câmp extern, diferit de zero, asupra dipolului se exercita un cuplu de forte al carui moment este care tinde sa aduca dipolul paralel cu câmpul extern, situatie în care energia potentiala devine minima .

6.2 Polarizarea electrica a dielectricului cu molecule nepolare

Vom considera un gaz monoatomic (un gaz mobil), ai carui atomi nu poseda un moment electric în absenta unui câmp exterior. Asa cum am vorbit în introducere, prin aplicarea unui câmp electric exterior atomii se polarizeaza:

fiind momentul electric dipolar indus. Acest tip de polarizare, în care norul electronic se deplaseaza, se numeste polarizare electronica. Daca ne imaginam un câmp electric exterior oscilant, ecuatia de miscare a centrului de sarcina se mai scrie:

unde este forta de revenire de tip elastic si este forta din partea câmpului electric exterior. Expresia complexa a câmpului oscilant este , cu frecventa unghiulara de oscilatie si solutia ecuatiei de miscare va fi: Introducând în ecuatie aceasta solutie obtinem:

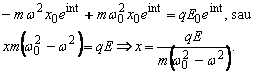
În aceasta expresie reprezinta frecventa unghiulara la care este absorbita lumina. În câmpuri neoscilante si deplasarea norului electronic este:

Momentul electric indus de atom este:

.

Comparând cu expresia: gasim expresia polarizabilitatii atomului:

Vectorul de polarizare, suma vectoriala a momentelor electrice dipolare din unitatea de volum se va calcula:

unde este concentratia gazului si este susceptibilitatea electrica a gazului. Din relatia

obtinem: Rezulta ca permitivitatea electrica a gazului este direct proportionala cu concentratia gazului si invers proportionala cu patratul frecventei optice a atomului. Acest rezultat constituie o aproximatie relativ buna în ciuda faptului ca am evitat complicatiile unei tratari cuantice exacte a problemei.

6.3 Polarizarea de orientare a dielectricului cu molecule polare

Sistemul analizat este alcatuit din molecule cu moment electric dipolar permanent (H₂O, NH₃,.). Datorita agitatiei termice momentele electrice sunt orientate practic si rezultanta lor este nula. Prin aplicarea unui câmp electric extern apare un moment electric indus datorat fortelor exercitate asupra electronilor (polarizare electronica) pe care îl vom neglija acum si un cuplu de forte care trebuie sa orienteze fiecare dipol paralel cu câmpul. Exista un bilant al celor doua tendinte opuse: de aliniere sub influenta câmpului aplicat si de dezaliniere datorita ciocnirilor termice ale moleculelor. Mecanica statistica afirma ca la echilibru termic numarul relativ de molecule care poseda energia potentiala este proportional cu factorul lui Boltzman:

Astfel numarul de molecule al caror moment electric dipolar formeaza unghiul cu câmpul electric raportat la unghiul solid este:

În conditii obisnuite exponentul este mic si facem aproximatia obtinând: . Integrând:

unde reprezinta numarul de molecule din unitatea de volum, concentratia gazului.

Înlocuind în integrala:

obtinem: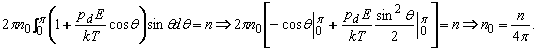

Polarizatia se calculeaza însumând vectorial momentele electrice din unitatea de volum. Rezultanta este orientata pe directia câmpului extern (componentele perpendiculare se compenseaza):

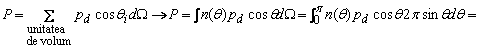
Polarizatia este direct proportionala cu E si invers proportionala cu T (legea lui Curie).

Avem deci: Putem extrage: relatie de asemenea verificata experimental. Daca se aplica un câmp electric oscilant momentele electrice dipolare vor tinde sa oscileze cu aceiasi frecventa. La frecvente înalte inertia moleculelor face ca acestea sa nu mai poata urma oscilatiile câmpului. În acest caz contributia momentului electric dipolar la înceteaza si ramâne doar cea datorata polarizabilitatii electrice, care se pastreaza datorita faptului ca electronii au inertia mica.