FENOMENE ELECTROMAGNETICE CU APLICATII IN TEORIA TRANSFORMATOARELOR SI MASINILOR ELECTRICE

S de a fi īntotdeauna nul; forma integrala este:

Forma locala a legii pentru domenii de continuitate a permeabilitatii magnetice este:

,

Īn puncte situate pe suprafete ce separa doua medii 1 si 2 cu permeabilitati magnetice diferite, forma locala a legii exprima conservarea componentei normale a inductiei magnetice ,

c. Legea conductiei electrice are formele locale:

, respectiv

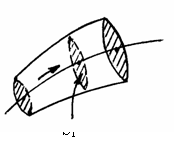
Prin integrarea formei locale īntre doua sectiuni transversale ale unui conductor, 1 si 2, parcurs de curentul , fig. 1.1, rezulta:

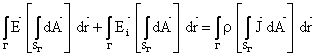
respectiv:

Īn cazul unui motor de curent continuu,

fig. 1.2 b), ; rezulta

relatia:

a) b) , sau

Fig. 1.2

d. Legea inductiei electromagnetice este asociata fenomenului generarii cāmpurilor electrice īn prezenta unor cāmpuri magnetice. Tensiunea electromotoare instantanee de-a lungul unei curbe īnchise G, u_eG , este egala cu viteza de scadere a fluxului magnetic F_SG printr-o suprafata deschisa oarecare S_G ce se sprijina pe curba G, antrenata de corpuri atunci cānd acestea se afla īn miscare. Forma integrala a legii este:

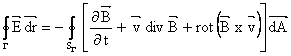
Componenta

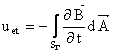
este denumita tensiune electromotoare de transformare, sau de pulsatie, iar

este tensiunea electromotoare de miscare. Valorile fiecarei din aceste doua componente depinde de referentialul īn raport cu care se studiaza fenomenul, īn schimb suma lor este independenta de sistemul de referinta.

Forma locala ale legii pentru domenii de continuitate a proprietatilor este: respectiv sunt:

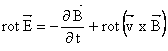
Pentru puncte situate pe suprafete ce separa doua domenii 1 si 2 cu proprietati diferite forma locala a legii are expresia:

a_i fiind denumita factor de acoperire polara. Valoarea medie a tensiunii electromotoare are expresia:

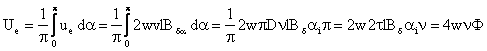
Daca masina are p poli, si .

e. Legea circuitului magnetic, care caracterizeaza generarea cāmpurilor magnetice, exprima faptul ca tensiunea magnetomotoare instantanee u_mG de-a lungul unei curbe īnchise G este egala cu suma dintre solenatia curentului de conductie q_SG si curentul de deplasare i_SGD , relative la o suprafata deschisa oarecare S_G ce se sprijina pe curba G. Forma integrala a legii este:

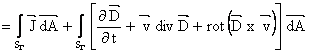
Legea circuitului magnetic are forma locala:

Īn regimul cvasistationar al cāmpului electromagnetic curentul de deplasare i_SGD este nul īn afara condensatoarelor, forma locala a legii īn domenii de continuitate a proprietatilor fiind:

respectiv

īn puncte situate pe supraete de separatie a doua domenii1si 2 cu proprietati diferite; este valoarea locala a paturii de curent electric de conductie.

Cāmpurile magnetice invariabile īn timp pot fi generate atāt cu ajutorul bobinelor parcurse de curent continuu, este cazul regimului de cāmp magnetic stationar, cāt si cu ajutorul magnetilor permanenti, īn cazul regimului de cāmp magnetostatic. Regimul de cāmp magnetic stationar este caracterizat prin ecuatiile:

Īn cazul regimului magnetostatic, cāmpul magnetic īn subdomeniile sursa - magneti permanenti este caracterizat prin ecuatiile:

Īn primul caz sursa cāmpului este reprezentata de valoarea locala a densitatii curentului electric de conductie, iar īn cel de-al doilea de dependenta locala , īn general neliniara, dintre magnetizatia si intensitatea a cāmpului magnetic.

Aplicatii

* Cāmpul magnetic produs de curentul continuu ce strabate un conductor cilindric circular, fig. 1.6, are expresiile:

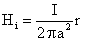, īn interiorul conductorului, si

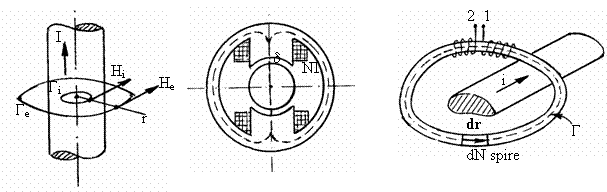
, īn exteriorul acestuia.

Fig. 1.6 Fig. 1.7 Fig. 1.8

** Inductia magnetica īn īntrefierul unei masini de curent continuu, fig. 1.7, rezulta din urmatoarea succesiune de relatii:

,

.

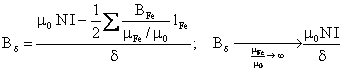*** Masurarea curentului cu ajutorul cordonului Rogowski, fig. 1.8. Cordonul Rogowski este un dispozitiv realizat prin īnfasurarea uniforma, spira lānga spira, a unui conductor izolat pe un tub flexibil nemagnetic. Cordonul īnconjoara conductorul al carui curent se masoara dupa un contur G arbitrar. Elementul de contur Gdr contine numarul de spire dN = N_sdr, unde N_s este numarul de spire pe unitatea de lungime a cordonului. Fluxul prin aceasta bobina elementara este . Fluxul total prin bobina - cordon Rogowski este:

Daca curentul i este continuu, masurarea fluxului F cu ajutorul unui fluxmetru conectat la bornele bobinei permite determinarea curentului . Daca curentul i este alternativ sinusoidal, , atunci fluxul variabil īn timp induce īn cordon tensiunea electromotoare:

Valoarea efectiva a acestei tensiuni, , este proportionala cu valoarea efectiva I a curentului.

f. Transformarea energiei īn conductoare aflate īn stare electrocinetica. Densitatea de volum a puterii instantanee, respectiv energia transformata īn unitatea de timp, are expresia:

unde p_J este energia transformata ireversibil īn caldura. Atunci cānd p_g > 0, energia interna se transforma īn energie electrica, iar cānd p_g < 0, energia electromagnetica se transforma īn energie interna.

Forma integrala a legii transformarii energiei īntre doua sectiuni ale unui conductor parcurs de curentul I este:

Pentru trei conductoare, reprezentānd un rezistor R, fig. 1.9 a), circuitul indusului unui generator de c.c., fig. 1.9 b), si circuitul indusului unui motor de c.c., fig. 1.9c), sunt prezentate alaturat relatiile care rezulta prin aplicarea legii.

g. Energia cāmpului electromagnetic si forte de natura electromagnetica. Energia cāmpului magnetic dintr-un volum dat este acea parte a energiei interne care se exprima numai īn functie de parametri electromagnetici de stare, respectiv de inductiile electrica si magnetica si de intensitatile cāmpurilor electric si magnetic .

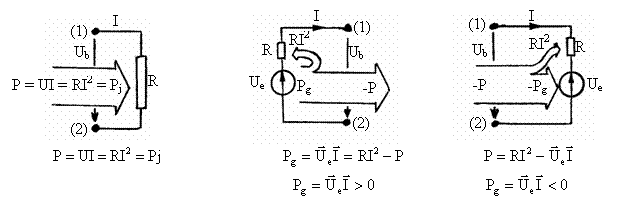
a) b) c)

Fig. 1.9

Scaderea - dW_em a energiei electromagnetice din volumul V_S īn timpul elementar dt este rezultatul urmatoarelor actiuni si efecte:

- lucrul mecanic efectuat de fortele si cuplurile de natura electromagnetica, dL_em = P_m dt , unde P_m este puterea mecanica dezvoltata īn V_S

- transformarea ireversibila a energiei electromagnetice īn caldura prin efect electrotermic, ;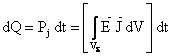

- transformarea ireversibila a energiei electromagnetice īn caldura prin efecte de histerezis electric si magnetic, dW_h = P_h dt;

- radiatia electromagnetica prin suprafata S a domeniului, 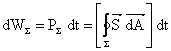, unde puterea radiata P_S a fost exprimata ca integrala pe S a unui vector .

Ecuatia bilantului energetic al volumului V_S are expresia:

Īn ipoteza ca īn V_S sunt corpuri imobile, P_m = 0, si nu prezinta fenomene de histerezis P_h = 0, rezulta:

Prin multiplicarea cu a formei locale a legii inductiei electromagnetice , si cu a legii circuitului magnetic, , rezulta prin sumare: .

Integrānd pe volumul V_S se obtine:

;

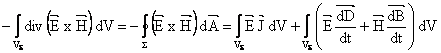prin identificare, rezulta:

si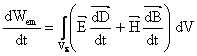