FIABILITATEA ECHIPAMENTELOR INDUSTRIALE

FIABILITATEA ECHIPAMENTELOR INDUSTRIALE

1. Introducere

Intrucat se lucreaza cu instalatii, echipamente si utilaje moderne si complexe, asigurarea unei uti­lizari eficiente si cit mai complete a acestora pe intreaga lor durata de functionare, reprezinta o conditie principala.

Daca prin calitatea unui produs intelegem gradul sau nivelul prin care acesta corespunde necesitatilor la un moment dat, atunci prin fiabilitate se intelege utilizarea produsului la parametrii proiectati, exploa­tarea lui sigura si continua, in conditii determinate, pe parcursul unei du­rate de timp date.

Conform definitiei Comisiei Electrotehnice Internationale (C.E.I.), fiabilitatea constituie caracteristica unui dispozitiv sau aparat, ex­primata prin probabilitatea cu care el indeplineste o functie necesara, in conditii date, pe o perioada de timp data.

Fiabilitatea se exprima printr-o functie care reprezinta probabilitatea evenimentului ca timpul T de functionare fara defectiuni sa depaseasca timpul t prescris, respectiv:

R(t)=P(T>t).

Aceasta functie are valoarea cuprinsa intre 0 si 1.

Fiabilitatea reprezinta totodata sinteza a patru notiuni:

probabilitate;

performanta si misiune de indeplinit;

conditii de functionare si exploa­tare;

timp de functionare prescris.

Notiunea de fiabilitate este strins le­gata si de notiunea de mentenabililate adica de acea proprietate a unui produs, exprimata prin proprietatea ca acesta sa poata fi int 515g68f retinut intr-o anumita perioada de timp.

Fiabilitatea constituie un parametru de sinteza a carui apreciere, in contextul cheltuielilor si termenelor de realizare se poate repre­zenta grafic printr-un triunghi FCT (fiabilitate, costuri, termene de rea­lizare), asa cum se arata in figura 1.

Fig.1. Triunghiul FCT

F-fiabilitate,

C-costuri,

T-termene de realizare

O notiune des intilnita in fiabilitate este notiunea de cadere, care constituie acel defect (avarie, deranjament, iesire din functiune, in­cident) care impiedica produsul sa-si indeplineasca una, mai multe sau toate functiunile de baza prevazute. Adica, nu orice defect al unui produs constituie o cadere.

Caderile se pot clasifica in:

caderi partiale care determina incetarea indeplinirii uneia sau mai multor functiuni de baza ale produsului fara a duce la scoaterea com­pleta din functiune a acestuia;

caderi totale care determina paralizarea tu­turor functiunilor de baza ale produsului si au ca efect scoaterea lui din functiune.

Dupa modul lor de aparitie caderile se mai pot clasifica in:

caderi instantanee, care apar intimplator si au la baza defecte ascunse ale produsului,

caderi progresive determinate de uzura, care apar treptat prin deplasarea parametrilor produ­sului de la limitele admise.

Evaluarea fiabilitatii se realizeaza in trei faze dis­tincte:

I. In faza de proiectare, pe baza considerentelor fiabilitate privind conceptia si proiectarea produsului precum si pe baza fiabilitatii componentelor sale in conditii de exploatare determinate; in aceasta faza avem in vedere fiabili­tatea preliminata (previzionala sau proiectata).

II. In faza de productie, pe baza incercarilor experimentale a produse­lor in laboratoare, statii de incercari, standuri de proba; in aceasta faza avem in vedere fiabilitatea experimentala sau tehnologica.

III. In faza de utilizare, pe baza informatiilor referitoare la comporta­rea produselor in exploatare, o anumita perioada de timp; in aceasta faza avem in vedere fiabilitatea operationala (efectiva la beneficiar).

Se mentioneaza si fiabilitatea nominala, care reprezinta fiabili­tatea unui produs prescrisa in specificatii (standarde, norme interne, ca­iete de sarcini etc).

2. Indicatorii statistici ai fiabilitatii

Acestia sunt:

timpul mediu de buna functionare (t);

abaterea medie patratica a timpilor de buna functionare ( _t

statistica caderilor;

functia experimanetala a fiabilitatii [R_N(t_i)];

rata experimentala a caderi­lor [λ_N(t_i)].

Timpul mediu de buna functionare

Timpul de buna functionare al produselor (masini, utilaje, instalatii aparate, componente etc.) este o variabila aleatoare care poseda o anumita lege de repartitie specifica fiecarui element. Stabilirea legii de repartitie se face pe baza unor cercetari si observatii statistice a timpului de functionare a produsului.

Consideram ca se studiaza modul de functionare a N elemente fa­bricate si utilizate in conditii identice. Vom nota cu t_i(i=;l, 2,,, N timpul de buna functionare a fiecarui produs pina la momentul caderii lui.

Rezultatul observarii se va concretiza printr-un sir de valori de forma: t_l, t₂,t_N, care reprezinta timpii de functionare ai elementelor observate.

Familia t(i=l, 2, N,) este finita si marginita, intrucat dupa o anumita perioada de timp T, toate elementele supuse observarii ies din functiune.

Numarul initial de elemente in functiune N, se micsoreaza dupa fiecare cadere cu o unitate.

Cu ajutorul timpilor de buna functio­nare se calculeaza timpul mediu de buna functionare (indicator statistic) (MTBF), cu relatia:

2.

In aceasta relatie numaratorul reprezinta suma timpilor de buna fuctionare a celor N elemente.

In cazul in care nu se poate inregistra timpul de buna functionare al fiecarui element supus cercetarii, datorita numarului mare de elemente, inregistrarea caderilor se face la anumite intervale de timp, Δt.

Daca presupunem ca observatia incepe la momentul t₀, in intervalul (t₀ , t₁) unde t₁ - t₀ Δt, cad K₁ elemente si ramin in functiune K*_t=N – K₁ . In intervalul (t_i—1, t_i), cad K_i elemente, iar in cursul intervalului (t_c-i , t_c) cad ultimele K_c elemente, astfel incat la momentul t_c al terminarii obser­vatiei cad toate cele N elemente

Rezulta:

Deci:   

Unde:

k_i - reprezinta elementele cazute.

Daca Δt reprezinta lungimea in­tervalului de observare, timpul mediu de buna functionare se de­termina cu relatia:

Daca timpul de buna functionare a celor N elemente observate se noteaza cu:

timpul mediu de buna functionare (MTBF) se mai poate calcula cu relatia:

MTBF se exprima in ore si se foloseste pentru realizarea de comparatii privind fiabilitatea intre produse similare.

Abaterea medie patratica a timpilor de buna functionare

Abaterea exprima gradul de imprastiere a timpilor de buna func­tionare si se calculeaza cu relatia:

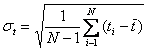
Acest indicator caracterizeaza uniformitatea nivelului de fiabilitate pentru o grupa de produse de acelasi fel.

Statistica caderilor

Repartitia statistica a caderilor, se realizeaza prin prelucrarea datelor observate, grupind aceste date pe inter­vale. In tabelul urmator se prezinta statistica caerilor.

Tabelul 1 Intervale de observare, frecvente absolute si relative ale caderilor

Histograma frecventelor ab­solute se traseaza trecandu-se pe axa absciselor intervalele de timp egale, iar pe axa ordonatelor numarul elementelor cazute.

Pe baza datelor din coloanele 1 si 2 ale tabelului se determina urmatorii indicatori statistici:

a) Frecventa absoluta cumulata a caderilor

Reprezinta numarul K_i de elemente defecte la momentul t_i. Numarul K_i se calculeaza cu relatia:

Reprezentarea grafica a acestui indicator se poate observa in fig. 3.

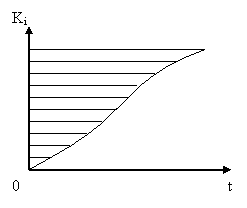Fig. 3. Frecventa absoluta cumulata a caderilor

b) Frecventa absoluta a elementelor in functiune

Cum la momentul de timp t_i suma dintre numarul de elemente cazute si numarul elementelor ramase in functiune (K*_i) este egala cu numarul total de elemente (N) supuse observarii, se calculeaza frecventa absoluta a elementelor in functiune cu expresia:

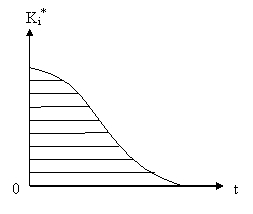Reprezentarea grafica se poate observa in figura 4.

Fig.4. Frecventa absoluta cumulata a elementelor ramase in functiune

c) Frecventa medie a caderilor

Indicatorul se determina cu relatia:

11

Acesta exprima intensitatea caderilor in unitatea de timp si reprezinta inversul indicatorului timpului mediu de buna functionare.

12

d) Frecventa relativa a caderilor

Inicatorul se calculeaza pentru fiecare interval de timp de observare cu expresia:

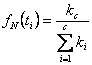13

e) Frecventa relativa cumulata a caderilor

Indicatorul exprima ponderea produselor cazute pina la momentul t_i din totalul celor N produse supuse observarii. Acesta se determina cu expresia:

14

Acest indicator este o functie crescatoare in scara, a carei valoare tinde catre 1, fiind egala cu 1, in momentul caderii ultimului element.

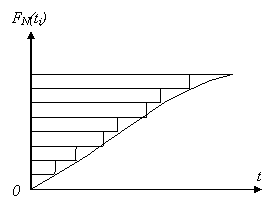
Fig.5. Frecventa relativa cumulata a caderilor

Functia experimentala a fiabilitatii

Functia experimentala a fiabilitatii R_N(t_i) se determina ca fiind raportul dintre frecventa absoluta a elementelor ramase in functiune la momentul t si numarul total de elemente N, respectiv

15

unde:

-reprezinta numarul produselor sau elementelor ramase in functiune la momentul t_i;

N -totalul produselor supuse observarii;

K_i -exemplare cazute pina la momentul t_i.

Cum , expresia (15) devine:

16

sau

17

La momentul t₀ cand incepe observarea, valoarea R_N(t_i) este egala cu unitatea intrucat:

18

Valoarea fiabilitatii scade, pe masura ce apar caderile, in urma scurgerii timpului, devenind egala cu zero, la momentul t_c, cind toate cele N elemente observate au cazut, adica:

19

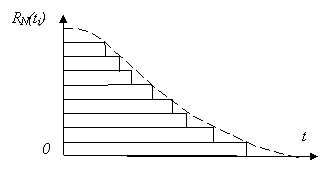
Fig.6. Graficul functiei experimentale de fiabilitate

Rata experimentala a caderilor

Acest indicator ne furnizeaza informatii in lega­tura cu fiabilitatea produsului la un moment dat si se de­termina cu relatia:

20

unde:

K_i - numarul elementelor cazute in intervalul de timp

(t_i+1 - t_i);

K^*_i-1 - numarul elementelor care nu au cazut pina la

momen­tul t_i-1.

In figura 7 este reprezentata rata experimentala a caderilor denumita si „curba cada de baie' ce se caracterizeaza prin existenta a trei perioade bine evidentiate:

I. Perioada initiala sau perioada de rodaj unde se evidentiaza caderile premature care au o frecventa ridicata (in aceasta perioada cad elementele cele mai slabe, cu defecte ascunse ce apar dupa un timp scurt de functionare)

II. Perioada normala sau perioada de viata utila, cu durata cea mai lunga (maturitate). In aceasta perioada caderile au un caracter aleator cu o rata scazuta si relativ constanta.

III. Perioda finala sau de uzura sau batrinete caracterizata printr-o cres­tere brusca a ratei caderilor datorita uzurii. In practica, s-a constatat ca, pentru unele utilaje si agregate tehnologice perioada finala nu se atinge datorita in special uzurii morale care duce la scoaterea lor din folosinta inainte de aceasta perioada.

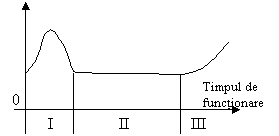
Fig.7. Rata experimentala a caderilor

3. Defectele instalatiilor electromecanice navale, dispozitivelor si componentelor acestora

Problema principala a functionarii instalatiilor electromecanice navale, utilizate si obtinerea unor indicatori de fiabilitate ridicati depinde in final de evitarea defectarii lor, precum si de reducerea la minimum a caderilor acestora.

Defectele sau iesirile din functiune se pot clasifica dupa mai multe categorii si anume:

caracterul remedierii defectiunii,

usurinta de depistare,

modul de aparitie,

cauze etc.

Dupa caracterul remedierii se evidentiaza:

defecte definitive care necesita repararea echipamentelor (elementelor) pentru restabilirea capa­citatii de functionare;

defecte intermitente, care apar ca urmare a mo­dificarilor accidentale si reversibile ale regimurilor de functionare.

Dupa dependenta dintre defecte se disting:

defecte primare;

de­fecte secundare, care apar ca rezultat a altor defecte.

Dupa usurinta de depistare avem:

defecte evidente,

defecte ascunse.

Dupa modul de aparitie se disting:

defecte bruste, care provoaca modi­ficarea brusca a caracteristicilor instalatiilor si utilajelor,

defecte treptate, care apar in urma deprecierii treptate a starii instalatiilor si utilajelor.

Dupa cauzele de producere, defectele pot fi:

accidentale,

dato­rate uzurii,

imbatrinirii etc.

Defectele provoaca scaderea productivitatii si randamentului instalatiilor si utilajelor industriale si se manifesta prin:

cresterea zgomotului si vibratiilor la toate tipurile de echipamente si utilaje;

deformatii plastice (alungire, comprimare, deformare) la organele de masini care functioneaza cu prestringeri mari supuse la sarcini mari;

fisuri si ruperi la oboseala la arbori, dintii rotilor dintate, rulmenti;

distrugeri datorita socurilor la organele de masini care functioneaza eu socuri;

distrugerea etansarilor la etansari hidraulice si pneumatice;

striviri datorita deformatiilor termice la rulmenti, angrenaje melcate, si suruburi cu bile;

uzura discurilor ambreiajelor, ghidaje si dantura rotilor dintate;

griparea ghidajelor si lagarelor de alunecare;

scaderea preciziei la masinile-unelte, motoare electrice, linii auto­mate;

scurtcircuite la masini, aparate si echipamente electrice.

4. Legile de repartitie a defectelor

4.1. Repartitii probabilistice clasice

Repartitiile probabilistice clasice pot fi:

repartitii discrete,

repartitii continue.

a. Repartitii discrete

Printre repartitiile discrete se evidentiaza:

repartitia binominala (Bernoulli),

repartitia polinominala,

repartitia binominala cu exponent negativ,

repartitia hipergeometrica,

repartitia Poisson.

Repartitia binominala (Bernoulli) denumita de multe ori schema urnei lui Bernoulli. Aceasta repartitie presupune n extrageri independente una de alta a unei bile dintr-o urna ce contine un numar de bile de doua culori. Independenta extragerilor se asigura, punindu-se de fiecare data din nou in urna bila extrasa.

Functia repartitiei binominale este de forma:

21

In aceasta relatie X este variabila aleatoare a repartitiei binominale.

Probabilitatea ca in n experiente independente, A sa apara de k ori iar (non A) de n - k ori este data de relatia:

22

Repartitia variabilei aleatoare X„ este data de relatia:

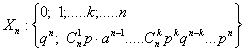
Probabilitatile reprezinta termenii dezvoltarii bi­nomului (p+p)ⁿ (de unde si denumirea de repartitie binomiala), respectiv:

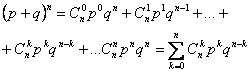24

Media si dispersia repartitiei binominale se determina cu expresiile:

in care:

n - reprezinta numarul de experiente sau elemente din

proba.

Calculul probabilitatilor repartitiei binominale se poate realiza si cu formula de recurenta:

26

Repartitia binominala este simetrica numai in cazul p=0,5, iar pentru alte valori este asimetrica, respectiv:

pentru p>0,5 asimetria este po­zitiva,

pentru p<0,5, asimetria este negativa.

Pe masura ce n creste repartitia binominala se simetri-zeaza.

Repartitia polinominala reprezinta o extindere a repartitiei binomi­nale. In urma a n incercari independente poate aparea unul din evenimentele:

A₁ de k₁ ori,

A₂ de k₂ ori,

A_n de k_n ori

Cu probabilitatile p₁, p₂,,p_n, constante la fiecare incercare.

Probabilitatea P_n(k₁, k₂, , k_m) ca evenimentul A₁ sa apara de k₁ ori, evenimentul A₂ de k₂ ori si asa mai departe pana la evenimentul A_m, care urmeaza sa aiba loc de k_m ori este data de expresia:

27

Media si dispersia repartitiei polinominale se determina cu expresiile:

cu 28

Repartitia binominala cu exponent negativ. La aceasta repartitie, evenimentelor de aparitie a defectelor li se atribuie probabilitatile:

Repartitia hipergeometrica. Aceasta este denumita si „schema bilei nere­venite'. Daca consideram ca intr-un lot de marime N se gasesc D rebuturi si N-D produse corespunzatoare cu D+(N-D)=N. Din lot se fac n ex­tractii succesive fara sa se introduca exemplarul verificat inapoi. Proba­bilitatea ca in n extractii succesive sa se obtina d rebuturi si n-d produse corespunzatoare cu d + (n—d)=n_, este data de expresia repartitiei hipergeometrice:

Functia de repartitie a variabilei X care urmeaza legea hipergeometrica este

Media si dispersia repartitiei se determina cu expresiile:

respectiv    32

Repartitia Poisson care mai este denumita si legea evenimentelor rare va fi studiata la un capitol ulterior.

b. Repartitii continue

Ca repartitii continue enumeram:

repartitia uni­forma,

repartitia normala,

repartitia lognormala,

repartitia Γ (gamma),

repartitia β (beta),

repartitia exponentiala negativa,

repartitia Weibull,

re­partitia Erlang,

repartitia χ² (hi patrat),

repartitia Student,

repartitia Snedecor,

repartitia Fischer,

repartitia Cauchy.

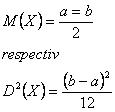
Repartitia uniforma. Aceasta are urmatoarea densitate de repartitie:

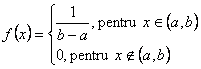
si functia de repartitie:

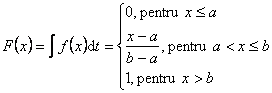34

Valoarea medie si dispersia variabilei aleatoare se determina cu expresiile:

35

in care: X este variabila aleatoare.

Repartitia normala. Prezentarea acestei repartitii se va face la capitol urmator.

Repartitia lognormala. Are urmatoarea densitate de repartitie

Valoarea medie si dispersia acestei repartitii sint date de expresiile:

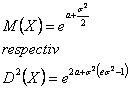37

in care este abaterea medie patratica.

Repartitia Γ (gamma). Aceasta repartitie are urmatoarea densitate de repartitie:

in care simbolul Γ(p), reprezinta functia GAMMA sau functia lui Euler de speta doua, definita cu ajutorul integralei improprii a lui Euler:

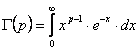
Valoarea medie si dispersia se determina cu expresiile:

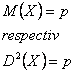
Repartitia β (beta). Aceasta are urmatoarea densitate de repartitie:

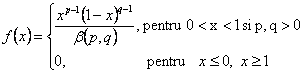
in care β (p,q) reprezinta functia lui Euler de prima speta, de variabile complexe p si q respectiv expresia.

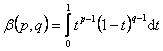
Intre functiile lui β(p,q) si Γ(p) exista relatia:

Tinind cont de expresia 43, realatia 41 se poate scrie sub forma:

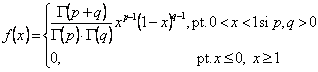
Valoarea medie si dispersia se determina cu expresiile:

Repartitia exponentiala negativa. Aceastaare densitatea de repartitie de forma:

46

Functia de repartitie are expresia:

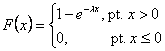
Valoarea medie si dispersia se determina cu expresiile:

48

Repartitia Erlang. Are urmatoarea densitate de repartitie:

49

Valoarea medie si dispersia se pot determina cu expresiile:

Repartitia Snedecor. Daca si sint doua variabile aleatoare indepen­dente repartizate χ², cu m grade de libertate, respectiv n grade de liber­tate, ambele cu parametrul , atunci variabila aleatoare, repartizata Sne­decor, va fi data de expresia:

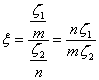51

Densitatea de repartitie se determina cu relatia:

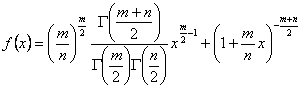
unde

Valoarea medie si dispersia se determina cu expresiile:

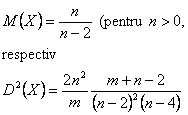53

Repartitia Fischer. Daca η este variabila aleatoare, avand repartitia Snedecor cu m, n grade de libertate, atunci variabila aleatoare

este repartizata Fischer cu m, n grade de libertate, cu densitatea de re­partitie urmatoare:

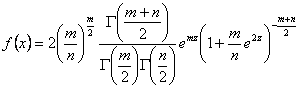
unde

Repartitia Cauchy. Aceasta are urmatoarea densitate de repartitie:

56

Aceasta repartitie este unimodala si simetrica fata de dreapta

4.2, Legi uzuale de repartitie a defectelor

Legile cel mai des intalnite sunt:

legea de repartitie Poisson;

legea de repartitie exponentiala;

legea de repartitie normala;

legea de repartitie Weibull;

legea de repartitie χ² (hi-patrat);

legea de repartitie Student.

Alegerea legii de repartitie a defectelor se face pe baza infor­matiilor obtinute cu privire la modificarile avute in interiorul elemen­telor si sistemelor inainte de aparitia defectiunilor.

Pentru descrierea legilor de repartitie este nece­sar sa se precizeze urmatoarele simboluri si definitii:

F(t) este functia de repartitie a timpului de functionare si respectiv probabilitatea ca un produs sa se defecteze in intervalul . Se estimeaza prin frecventa relativa cumulata F_N(t);

f(t) reprezinta probabilitatea ca variabila aleatoare X sa ia valoa­rea t, daca variabila este discreta, sau densitatea de repartitie daca va­riabila este continua. Se estimeaza prin frecventa relativa f_N(t);

R(t), este functie de fiabilitate adica probabilitatea ca un produs sa functioneze fara defectare in intervalul (0, t), in conditii determinate: R(t)=P(T>t);

λ(t) reprezinta rata sau intensitatea de defectare si se expri­ma prin limita raportului dintre probabilitatea de defectare in intervalul (t, t+ Δt) si marimea intervalului Δt, cind Δt→0, adica

57

Se estimeaza prin rata experimentala de defectare λ_N(t).

Legea de repartitie Poisson

Aceasta lege are un caracter discret (legea evenimentelor rare) si se caracterizeaza prin aceea ca probabilitatea p a aparitiei caracteristicii observate este rara.

Probabilitatea aparitiei a k defecte in timpul t se exprima prin densi­tatea de probabilitate

unde: este o constanta care exprima cit de rare sunt defectele.

Media si dispersia repartitiei Poisson se determina cu expresiile:

M(X)=X, respectiv D²(X)=A

Functia de repartitie a variabilei aleatoare X, care urmeaza legea Poisson, se scrie:

60

Legea de repartitie exponentiala

In aceasta lege probabilitatea de defectare in orice interval Δt este proportionala cu lungimea intervalului, nedepinzand de timpul scurs de la punerea in functiune ci doar de buna functionare pina in acel moment, respectiv:

Densitatea de repartitie a legii exponentiale este dat[ de relatia:

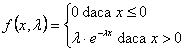
Functia de repartitie a timpului de functionare se obtine cu expresia:

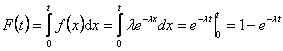
Functia de fiabilitate se determina cu ajutorul expresiei:

intrucat R(t)+F(t) = l.

Rata de defectare , va rezulta din expresia:

Media si dispersia repartitiei exponentiale se pot determina cu expresiile:

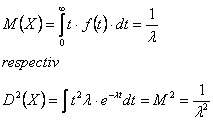
Timpul mediu de buna functionare se determina cu expresia:

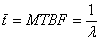
Aceasta conduce la o noua relatie a functiei fiabilitatii, respectiv:

Legile de repartitie Poisson si exponentiala sunt caracteristice pentru perioada de viata utila.

Legea de repartitie normala

Atit teoria cit si practica au pus in evi­denta ca pentru perioada finala sau de uzura a unui produs, pentru caracterizarea fiabilitatii se poate utiliza legea normala. Repartizarea tim­pilor de defectare in ambele sensuri, in jurul unei valori mediane se realizeaza datorita influentelor exterioare, a conditiilor de productie diferite in care sunt exploatate instalatiile aceluiasi lot.

Densitatea de probabilitate in cazul legii normale se calculeaza cu expresia:

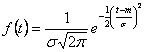
in care:

m -reprezinta media;

-dispersia repartitiei normale.

Functia de repartitie sau probabilitatea caderii produsului

pina la mo­mentul t, se determina cu expresia:

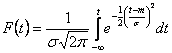70

iar functia de fiabilitate se determina cu expresia:

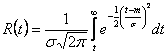71

Rata caderilor se obtine cu expresia:

72

Legea de repartitie Weibull

Cand defectele care apar nu pot fi caracterizate cu legea exponentiala sau cu legea normala, intrucat ele sunt rezultatul unor repartitii de amestec, corespunzatoare faptului ca unele din elemente sunt uzate, in timp ce altele nu si-au inceput inca viata utila.

Pentru a caracteriza astfel de situatii matematicianul Weibull a propus, pentru timpul pina la prima defectare repartitia cu densitatea, respectiv expresia:

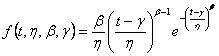73

in care:

β -este un parametru de forma numit panta, care

determina forma repartitiei;

-este un parametru de scara;

γ - reprezinta un parametru de pozitie.

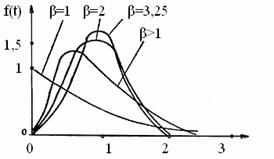
Fig Graficul functiei de repartitie Weibull pen­tru diferite valori ale parametru­lui β

pentru β=l, legea Weibull din (73) coincide cu legea exponen­tiala.

pentru β>l, curba de repartitie este concava, luind alura unui clo­pot cu cit β creste.

pentru β=3,25 legea Weibull coincide cu legea normala.

Functia de repartitie, pentru legea Weibull, se determina cu expresia:

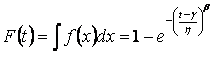74

Daca tinem cont de expresia 74 probabilitatea ca evenimentul (defectul) sa se produca in intervalul de timp (γ, t), respectiv probabilitatea functionarii fara caderi a unui echipament, pina la momentul t este data de expresia:

75

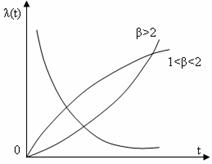
Fig Rata defectiunilor pentru diferite valori ale parametrului de forma β.

In figura .. se reprezinta rata defectiunilor pentru diferite valori ale parametrului de forma β.

Media si dispersia repartitiei Weibull se calculeaza cu expresiile:

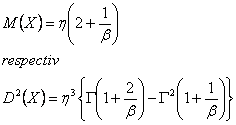76

In tabele se gasesc valorile functiei Γ (x).

In situatia in care la un echipament se descopera defectiuni ascunse, iar apoi un timp indelungat nu sufera de „imbatrinire', probabilitatea caderii la inceput este foarte ridicata, dupa care se stabilizeaza in jurul unui nivel relativ constant. In aceste conditii, functia de fiabilitate R(t) a echipamentului se aproximeaza bine cu legea Weibull ce are parametrul β<t.

Cand echipamentele observate se caracterizeaza prin absenta defectelor ascunse, insa manifesta pe masura scurgerii timpului un proces intens de imbatrinire, intensitatea defectarilor creste monoton, iar functia fiabilitatii se aproximeaza prin legea Weibull avand parametrul β>l.

Determinarea parametrilor pentru o lege Weibull se face pe baza ob­servarii timpului de functionare pentru un lot de N elemente.

Estimarea parametrilor se face cu ajutorul metodei celor mai mici pa­trate sau pe cale grafica, cu ajutorul diagramei Allan Plait. Aceasta diagrama este intocmita prin efectuarea unor logaritmari repetate asupra functiei de fiabilitate.

Legea de repartitie χ² (hi patrat)

Cand in controlul defectelor produselor intervin sume de patrate ale variabilelor aleatoare X_l, X₂, ,X_i independente, ce urmeaza fiecare o lege normala cu media „O' si dispersia , respec­tiv N(0, ), atunci repartitia unei astfel de sume se noteaza astfel:

77

Aceasta expresie este denumita repartitia „hi patrat' cu l grade de libertate.

Valoarea medie si dispersia variabilei χ² este calculata cu expresiile:

78

Legea de repartitie Student

O variabila aleatoare (defect in cazul nostru) urmeaza o repartitie Student (notata t), cu l grade de libertate daca densitatea de repartitie este data de functia urmatoare:

79

Parametrul repartitiei t este numarul gradelor de liber­tate l

Functia de repartitie, corespunzatoare legii Student este:

80

daca inlocuim x cu t se obtine:

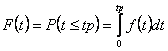
Denumirea de Student vine de la pseudonimul matematicianului englez Gosset.

Estimarea parametrilor de fiabilitate

Controlul fiabilitatii echipamen­telor si instalatiilor precum si a elementelor com­ponente a acestora consta in verificarea conformitatii cu normele si standar­dele de produs. Pentru aceasta se folosesc metode de in­cercari prin sondaj si anume:

incercari cenzurate (k), la care experimentul se opreste in momentul cind din cele n produse care alcatuiesc esantionul au cazut k produse (k este un numar prealabil stabilit);

incercari limitate sau trunchiate (T), la care experimentul se opreste la un moment de timp T stabilit in prealabil.

Ambele tipuri de incercari se pot efectua cu:

inlocuirea componentelor cazute (C),

fara inlocuirea componentelor cazute (F).

Tinind cont de modul de organizare al incercarilor susmentio­nate rezulta tipurile de planuri de incercari prin sondaj urmatoare:

planuri cenzurate de incercari fara inlocuire (n, F, k);

planuri cenzurate de incercari cu inlocuire (n, C, k);

planuri trunchiate de incercari fara inlocuire (n, F, T);

planuri trunchiate de incercari cu inlocuire (n, C, T).

Cu ajutorul informatiilor obtinute din incercarile de fiabilitate prin sondaj efectuate pentru un anumit element si cunoscindu-se legea de repartitie, se trece la etapa estimarii fiabilitatii si a testarii ipotezelor teoretice cu datele rezultate din experimentari.

Legea de repartitie cel mai des aplicata in modelarea fenomenelor de fiabilitate este legea exponentiala. Aceasta are ca explicatie faptul ca in perioada utila de functionare a echipamentelor si instalatiilor electromecanice, pentru care se fac studiile de fiabilitate, intensitatea cade­rilor se poate considera constanta.