Geometria danturilor evolventice interioare

Geometria danturilor evolventice interioare

♦ o evolventa interioara γ₂ fata de cercul cu convexitate în punctul de contact C - polul angrenarii.

♦ o evolventa interioara γ₁ fata de cercul cu concavitate în punctul de contact C - figura 10.38.

Forma geometrica a danturii plane interioare corespunde cu copia negativă 929e42j ; a danturii plane exterioare cu acelati modul, numar de dinti si marime a deplasarii fig. 10.39. Diferenta consta în pozitia racordarii, care tin în acest caz este la baza dintelui. Dimensiunile danturii evolventice interioare se exprima prin relatiile:

În general raza de curbura a unei curbe

Daca dantura nu este deplasata

sau

gradul de acoperire total fig. 10.41

a)      pentru z₁≥30 x_n1= x_n2=0

b)      z₁<30 si z₁+ z₁≥60

c)      z₁>10 si 30<z₁+ z₁<60

d)      z₁+ z₁<30

Coeficientul axial Ψ_a, diametral Ψ_d sau modular Ψ_mn, al latimii danturii

Tabelul10.13

Latimea danturii

Arcul frontal de divizare al dintelui

VERIFICAREA SUBTĂIERII DINŢILOR

Numarul de dinti echivalent

Numarul minim de dinti

pentru

Coeficientul deplasarii minime de profil

pentru

VERIFICAREA INTERFERENŢEI DINŢILOR

Diametrul începutului evolventic

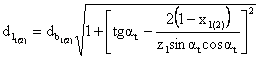
Diametrul începutului angrenarii

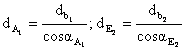
unde

Pentru a nu aparea interferenta este necesar ca:

VERIFICAREA CONTINUITĂŢII ANGRENĂRII

Gradul de acoperire al profilului

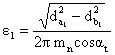
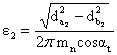
Se recomanda

Gradul de acoperire datorat înclinarii dintilor

Gradul de acoperire total

VERIFICAREA JOCULUI LA CAP

Jocul la cap la functionare

Este necesar ca

Coeficientul scurtarii capului dintelui

Pentru a se realiza jocul de referinta

Pentru a se realiza un joc

unde

VERIFICAREA GROSIMII DINŢILOR PE CERCUL DE CAP

Arcul normal de cap al dintelui

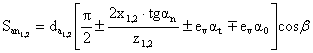
unde

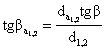este necesar ca

la danturi îmbunatatite

la danturi durificate