MULTIMI CLARE SI MULTIMI VAGI

Obiectiile filosofice pot fi crescute de implicatiile logice ale formarii unei structuri matematice pe premiza neclaritatii, de aceea pare (cel putin superficial) necesar sa ceara daca un obiect este sau nu este element al unei multimi date. Din punct de vedere estetic, aceasta poate fi cea mai satisfacatoare situatie a problemelor, dar inlr-o masura incat structurile matematice sunt folosite la modelarea realitatilor fizice, este de obicei o cerinta ireala... Multimile vagi au o baza filosofica plauzibila prin intuitie. O data ce aceasta este acceptata, consideratiile analitice si practice despre multimile vagi sunt in majoritatea privintelor total ortodoxe.

James Bezdek Profesor, Computer Science, 1981

Avand in vedere Capitolul 1, universul prelegerii este universul informatiei disponibile la o problema data. O data ce acest univers este definit, suntem capabili sa definim anumite evenimente la aceasta informatie spatiu. Vom descrie multimile ca abstractiuni matematice ale acestor evenimente si ale universului insusi. Figura 2.1a arata o abstractiune a prelegerii, se spune X, si o multime clara A undeva in acest univers. O multime clara este definita de limite precise; de exemplu nu este nici o incertitudine in prescriptia si localizarea limitelor multimii, dupa cum se vede in figura 2.1a unde limita multimii clare A este o linie clara. O multime vaga, pe de alta parte, este fixata de proprietati vagi sau ambigue; pornind de aici limitele ei sunt specificate ambiguu, dupa cum sunt aratate de limita vaga pentru multimea A in figura 2. 1b.

In Capitolul 1 am introdus notiunea de multime de apartenenta, din punct de vedere unidimensional. Din nou figura 2.1 ne ajuta sa explicam aceasta idee, dar dintr-o perspectiva bidimensionala. Punctul a in figura 2. 1a este clar un membru al multimii clare A; punctul b este clar ca nu este un membru al multimii A. Figura 2.1b arata limita vaga, ambigua a multimii vagi A in acelasi univers X; limita inchisa reprezinta regiunea limita a lui A. In regiunea centrala (neinchisa) a multimii vagi, punctul a este clar un membru complet al multimii. In afara regiunii limita a multimii vagi, punctul b este clar nu un membru al multimii vagi. Oricurn apartenenta punctului c, care este pe regiunea limita, este ambigua. Daca apartenenta completa intr-o multime (precum la punctul a in figura 2.1b) este reprezentata de numarul 1 si non-apartenenta intr-o multime (precum punctul b in figura 2. 1b) este reprezentata de 0, atunci punctul c in figura 2.1b trebuie sa aiba o valoare intermediara a apartenentei (apartenenta partiala in multimea vaga A) pe intervalul [0,1]. Probabil apartenenta punctului c in A se apropie de valoarea lui 1 cand se muta mai aproape de regiunea centrala (neinchisa) in figura 2. 1b a lui A si apartenenta punctului c in A se apropie de valoarea lui 0 cand se muta mai aproape de parasirea regiunii limita a lui A.

In acest capitol, principiile si operatiile multimilor vagi sunt comparate cu acelea ale multimilor clare. Mai multe carti bune sunt disponibile pentru revederea acestui material de baza [vezi de exemplu Dubois si Prade, 1980; Klir si Folger, 1988; Zimmerman, 1991]. Multimile vagi accepta virtual toate (cu o exceptie cum se va vedea) definitiile, principiile si axiomele care definesc multimile clare. Cum s-a indicat in Capitolul 1, multimile clare sunt o forma speciala a multimilor vagi; ele sunt multimi fara ambiguitate in apartenenta lor (de exemplu ele sunt multimi cu linii clare). Se va arata ca teoria fuzzy este o teorie matematic riguroasa si comprehensiva folositoare in caracterizarea conceptelor (multimi) cu ambiguitate naturala. Este instructiva

introducerea multimilor vagi la prima revedere a elementelor teoriei multime clara.

MULTIMI CLARE

Se defineste universul prelegerii, X, ca o colectie de obiecte avand toate aceleasi caracteristici. Elementele individuale in universul X pot fi indicate cu x.Trasaturile elementelor din X pot fi discrete, intregi numarabile sau cantitati continue apreciate pe linia reala. Exemple de elemente ale universurilor variate pot fi dupa cum urmeaza:

Viteza ceasului computer-ului

Curentii de comanda ai unui motor electronic

Temperatura de comanda a masinii termice (in grade Celsius)

Magnitudinea Richter a unui cutremur

Intregii de 1 la 10

Cele mai multe procese tehnologice din realitate contin elemente reale si nenegative (pozitive). Primele patru elemente abia numite sunt exemple de astfel de elemente. Oricum, pentru scopuri de modelare, majoritatea problemelor tehnologice sunt simplificate la considerarea doar a valorilor intregi a elementelor intr-un univers al prelegerii. Asa, de exemplu, viteza ceasului computer-ului poate fi masurata cu valori intregi in megaHertz si temperaturile masinii termice pot fi masurate cu valori intregi in grade Celsius. Mai departe, majoritatea proceselor tehnologice sunt simplificate sa se considere doar dimensiunile finite. Cu toate ca magnitudinile Richter nu pot avea o limita teoretica, noi nu am masurat istoric magnitudinile cutremurelor mult deasupra lui 9; aceasta valoare poate fi limita superioara intr-o problema de desen (plan) structural tehnologic. Ca un alt exemplu, presupuneti ca sunteti interesati de forta de sub un picior al scaunului pe care stati. Puteti argumenta ca este posibil sa primiti o forta infinita pe un picior al scaunului, stand pe scaun intr-o asa pozitie incat doar un picior al scaunului va sustine si lasand suprafata capatului acelui scaun sa se apropie de zero. Cu toate ca e teoretic posibil, in realitate piciorul scaunului ori se va indoi elastic cand extremitatea suprafetei devine foarte mica ori nu va rezista plastic si va esua deoarece materialele care au putere infinita nu au fost inca extinse. Asadar, alegand un univers care este abstract si finit sau unul care este continuu si infinit este o alegere de modelare; alegerea nu modifica caracterizarea multimilor definite pe univers. Daca elementele unui univers sunt continue, atunci multimile definite pe univers vor fi compuse din elemente continue. De exemplu, daca universul prelegerii este definit ca toate magnitudinile Richter pana la valoarea 9, atunci putem defini o multime de "magnitudini distinctive", care pot fi compuse (i) din toate magnitudinile mai mari sau egale cu 6 in cazul clar sau (ii) din toate magnitudinile "aproximativ 6 si mai inalte" in cazul vag.

O calitate folositoare a multimilor si universurilor pe care ele sunt definite este un versificator cunoscut sub numele de putere sau numar cardinal. Numarul total al elementelor dintr-un univers X se numeste numarul sau cardinal, notat cu n_x unde din nou x este o inscriptie pentru elementele individuale din univers. Universurile diferite care sunt compuse dintr-o colectie finita de elemente vor avea un numar cardinal finit; universurile continue care includ o colectie infinita de elemente vor avea un numar cardinal infinit. Colectiile de elemente in interiorul unui univers sunt numite multimi si colectiile de elemente din interiorul unor multimi sunt numite submultimi. Multimile si submultimile sunt termeni folositi de obicei ca sinonime, de cand orice multime este de asemenea o submultime a multimii universale X. Colectia tuturor elementelor din univers mai este numita si multime intreaga.

Pentru multimile clare A si B alcatuite din colectii de cateva elemente din X, urmatoarea notatie este definita:

x X x apartine lui X

x A => x apartine lui A

x A x nu apartine lui A

Pentru multimile A si B din X avem de asemenea:

A B => A este inclusa strict in B (daca x A, atunci x B )

A B A este inclusa in sau egala cu B

A=B A B si B A

Definim multimea vida, , ca fiind multimea ce nu contine nici un element si intreaga multime, X, ca fiind multimea tuturor elementelor din univers. Multimea vida este asemanatoare cu un eveniment imposibil si intreaga multime este asemanatoare cu un anumit eveniment. Toate multimile posibile ale lui X constituie o multime speciala numita multimea putere, P(X). Pentru un univers X, multimea putere P(X) este enumerata in exemplul urmator.

Exemplul 2.1. Avem un univers ce cuprinde 3 elemente, X = deci numarul cardinal este n_X = 3. P(X) = , , , , } Numarul cardinal al multimii putere, notat n_P(X) , este gasit ca fiind:

n_P(X) = 2 ⁿ_x = 2³ = 8

ATENTIE!

Daca numarul cardinal al universului este infinit, atunci numarul cardinal al multimii putere este de asemenea infinit; de exemplu n_x = => n_P(x) =

OPERATII CU MULTIMI CLARE

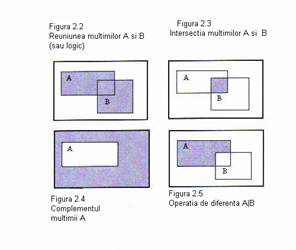
Fie A si B doua multimi din universul X. Reuniunea dintre doua multimi, notata A B, reprezinta totalitatea elementelor din univers care se afla (sau apartin) multimii A, multimii B sau multimilor A si B. (Aceasta operatie se mai numeste si sau logic; o alta forma de reuniune este si operatia sau exclusiv. Operatia sau exclusiv va fi descrisa in capitolul 7). Intersectia celor doua multimi, notata A B, reprezinta totalitatea elementelor universului X care simultan se afla (sau apartin) atat multimii A, cat si multimii B. Complementul multimii A, notat Ā, se defineste ca totalitatea elementelor din univers care nu se afla in multimea A. Diferenta dintre multimea A si multimea B, notata A | B, se defineste ca suma elementelor universului care se afla in A, dar nu se afla in B. Aceste operatii sunt prezentate mai jos sub forma de multimi teoretice:

Reuniune A B=     (2.1)

Intersectie         A B = (2.2)

Complement Ā = (2.3)

Diferenta A B =                         (2.4)

Aceste patru operatii sunt prezentate sub forma de diagrame Venn, in figurile 2.2 -2.5.

PROPRIETATILE MULTIMILOR CLARE

Anumite proprietati ale multimilor sunt importante datorita influentei lor asupra folosirii multimilor in matematica. Cele mai reprezentative proprietati pentru definirea multimilor clare si care arata asemanarea lor cu multimile vagi, sunt urmatoarele:

Comutativitatea A B = B A                                                    (2.5)

A B = B A
Asociativitatea       A (B C) = (A B) C                     (2.6)

A (B C) = (A B) C

Distributivitatea A (B C) = (A B) (A C)            (2.7)

A (B C) = (A B) (A C)

Idempotenta         A A = A                                                    (2.8)

A A = A

Identitate             A = A (2.9)

A X = A

A X = X

A

Tranzitivitate       Daca A B C, atunci A C          (2.10)

Simbolul " " inseamna inclus in sau echivalent cu; simbolul " inseamna doar inclus in.

Stagnare A = A                   

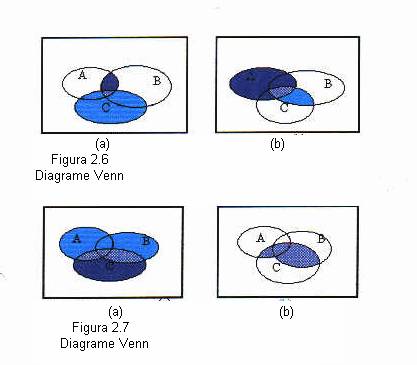
Suprafata dublu hasurata in figura 2.6 este un exemplu de diagrama Venn a proprietatii de asociativitate pentru intersectie si suprafetele dublu hasurate in figurile 2.7 si 2.8 sunt exemple de diagrama Venn a proprietatii de distributivitate pentru combinatii variate ale proprietatilor de intersectie reuniune.

Doua proprietati speciale ale operatiilor cu multimi sunt cunoscute ca legile tertului exclus si legile lui De Morgan. Aceste legi sunt enumerate aici pentru doua multimi A si B. Legile tertului exclus sunt foarte importante deoarece acestea sunt singurele operatii cu multimi descrise aici care nu sunt valabile pentru ambele multimi: multimi clare si multimi vagi (fuzzy). Exista doua legi ale tertului exclus (date in ecuatiile [2.12]). Prima, numita legea tertului exclus, are de a face cu reuniunea dintre o multime A si complementul ei ; a doua, numita legea contradictiei, reprezinta intersectia unei multimi A cu complementul ei.

Legea tertului exclus          A Ā =X                            (2.12a)

Legea contradictiei       A (2.12b)

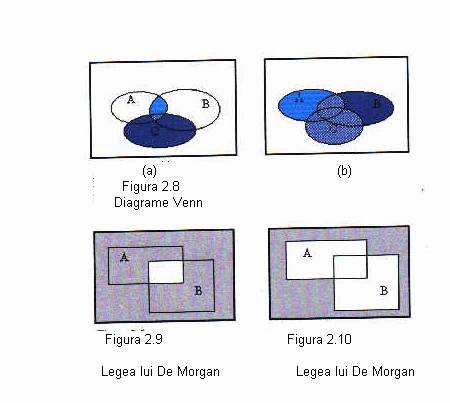
Legile lui De Morgan sunt importante din cauza utilitatii lor in demonstrarea tautologiilor si contradictiilor in logica, ca o gazda a operatiilor cu alte multimi si probe. Legile lui De Morgan sunt prezentate in suprafetele inchise ale diagramelor Venn in figurile 2.9 si si sunt descrise matematic in ecuatiile 2.13.

_____ _ _

A B = A B         (2.13a)

_____ _ _

A B = A B      (2.13b)

In general, legile lui De Morgan pot fi stabilite pentru n multimi cum sunt asigurate aici pentru evenimente, E_n:

E₁ E ₂ E₃.. E_n = E, E₂ E₃... E_n                        (2.14a)

E₁ E₂ E₃... E_n = E, E₂ E₃... E_n (2.14b)

Din ecuatiile generale, ecuatiile 2.14, pentru legile lui De Morgan obtinem o relatie de dualitate: complementul unei reuniuni sau intersectii este egal cu intersectia sau respectiv reuniunea complementilor respectivi. Acest rezultat este foarte puternic in legatura cu structurile multimii deoarece avem de obicei informatii despre complementul unei multimi (sau unui eveniment) ori complementul unor combinatii a multimilor (evenimentelor), decat informatiile despre multimile insele.

Exemplul

Un arc fara adancime consta in doi membri ascutiti asa cum se vede in figura 2.1. Daca vreun membru esueaza, atunci arcul se va prabusi. Daca E₁ = supravietuirea membrului 1 si E ₂ = supravietuirea membrului 2, atunci supravietuirea arcului = E₁

E₂ si invers prabusirea arcului = E, E₂. Logic, ca prabusirea arcului se va

petrece daca oricare dintre membrii esueaza, de exemplu cand E, E₂ . Prin urmare,

E, E₂ = E, E₂ , care este o ilustratie a legii lui De Morgan .

Asa cum sugereaza ecuatia 2.14, legile lui De Morgan sunt foarte folositoare pentru evenimente compuse, asa cum este ilustrat in exemplul urmator.

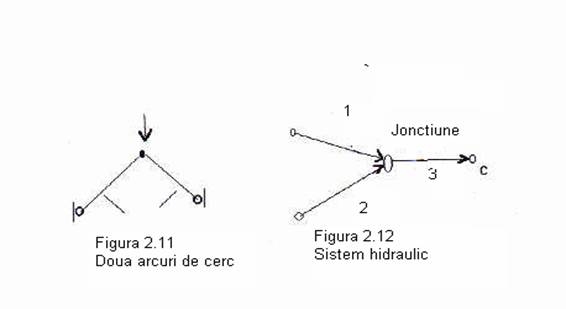
Exemplul 2.3

Din scopuri de siguranta, fluidul livrat de o pompa hidraulica C intr-un avion vine din doua linii sursa redundante, A si B. Fluidul este transportat de tuburi cu presiune ridicata constand din bratele 1, 2 si 3 dupa cum se arata in figura 2.12. Listele de manipulare ale pompei arata ca fiecare linie sursa singura este capabila sa livreze presiunea fluidului necesara pompei. Notand cu E₁= esecul bratutui 1, E₂=esecul bratului 2 si E₃=esecul bratului 3. Atunci presiunea insuficienta pentru a manipula pompa va fi produsa de(E, E₂) E₃ si presiunea suficienta va fi complementul acestui eveniment.

Folosind legile lui De Morgan, putem calcula conditia presiunii suficiente ca fiind

(E, E₂) E₃ = (E₁ E ₂ ) E₃

unde (E₁ E₂] inseamna disponibilitatea presiunii la jonctiune si E₃ inseamna absenta esecului in bratul 3.

Aplicatiile multimilor clare la functii

Aplicatia este un concept important in relationarea formelor multimii teoretice la reprezentarea functiei teoretice a informatiei. In forma sa generala poate fi folosita la aplicarea elementelor sau submultimilor dintr-un univers al prelegerii la elementele sau submultimile dintr-un alt univers. Se presupune ca X si Y sunt doua universuri ale prelegerii (informatiei) diferite. Daca un element x este continut in X si corespunde unui element y continut in Y, este numita general o aplicatie de la X la Y sau f : X Y. Ca o aplicatie, functia (indicator) caracteristica c_A este definita

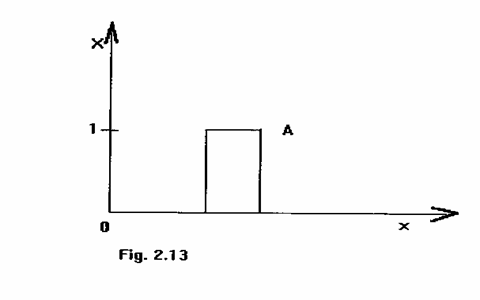
unde c_a exprima "apartenenta" pentru un element x din univers. Aceasta idee de aparteneta este o aplicatie de la un element x din universul X la unul din cele doua elemente din universul Y; de exemplu la elementele 0 sau 1, dupa cum se arata in figura 2.13.

Pentru orice multime A definita pe universul X, exista o multime functie teoretica, numita multime valoare, notata V(A), sub aplicatia functiei caracteristice, c . Conventional, multimii vide ii este atribuita apartenenta valorii 0 si multimii intregi ii este atribuita apartenenta valorii 1. 14414y2421o

Exemplul 2.4

Continuand cu exemplul (exemplul universului cu trei elemente X = dorim sa aplicam elementele multimii putere a lui X, de exemplu P(X),

unui univers, Y, ce contine doar doua elemente (functia caracteristica),

Y=

Ca mai inainte, elementele multimii putere sunt enumerate. P(X)=,,,,,,}

In acest fel, elementele in multimea valoare V(A) determinate din aplicatie sunt:

V=,,,,,,,}

De exemplu, a treia submultime in multimea putere P(X) este elementul b. Pentru aceasta submultime, nu este un a, deci valoarea lui 0 merge in prima pozitie a retelei de trei informatii; este un b, deci valoarea lui 1 merge in pozitia a doua a retelei de trei informatii; si nu este nici un c, deci valoarea lui 0 merge in pozitia a treia a retelei de trei informatii. Mai departe, a treia submultime a multimii valoare este reteaua de trei informatii, dupa cum s-a vazut deja. Multimea valoare are un grafic analog care este descris la sfarsitul capitolului in sectiunea "Multimi ca puncte in spatii cu mai multe dimensiuni."

Acum se definesc doua multimi A si B din universul X. Reuniunea acestor doua elemente in termenii functiei teoretice este data dupa cum urmeaza (simbolul v este operatorul maxim si este operatorul minim):

Reuniunea

a b->c_{A B}(x) = c_A (x) c_b(x) = max(c_A(x),c_B(x))

Intersectia acestor doua multimi in termenii functiei teoretice data de:

Intersectia

Complementul unei singure multimi in universul X, sa spunem A, este dat
de:
Complementul A - > c _A (x) = 1 - c_a (x)           (2.18)

Pentru doua multimi ale aceluiasi univers, sa le numim A si B, daca o multime (A) este continuta in alta multime (B), atunci:

Incluziune A B c_A(x) c_B(x)

Operatorii functiei teoretice pentru reuniune si intersectie (altii decat maximul si respectiv, minimul) sunt discutati in literatura [Gupta si Qi, 1991].

In multimile clare sau precise, trecerea unui element din universul dintre apartenenta si non-apartenenta intr-o multime data este abrupta si bine definita (spusa a fi "clara"). Pentru un element dintr-un univers care contine multimi vagi aceasta trecere poate fi gradata. Aceasta trecere printre gradele (valori) variate ale apartenentei poate fi gandita conform faptului ca limitele multimilor neclare (vagi) sunt vagi si ambigue. De aici incolo, apartenenta unui element din univers in aceasta multime este masurata de o functie care incearca sa descrie ambiguitatea si neclaritatea.

O multime vaga, atunci, este o multime ce contine elemente care au grade (valori) variabile ale apartenentei in multime. Aceasta idee este in contrast cu multimile clare sau precise, deoarece membrii unei multimi precise nu vor fi membrii decat daca apartenenta lor era plina sau completa, in acea multime(de exemplu apartenentei lor ii este atribuita valoarea 1). Elementele dintr-o multime vaga, deoarece apartenenta lor nu este neaparat nevoie sa fie completa, pot fi de asemenea membrii unei alte multimi vagi din acelasi univers.

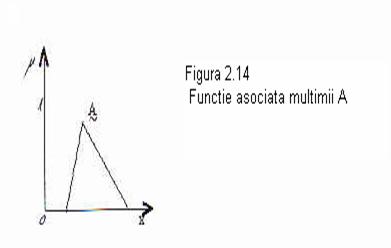
Elementele unei multimi vagi sunt aplicate unui univers al valorilor de apartenenta folosind o forma a functiei teoretice. Asa cum a fost mentionat in Capitolul 1 (ecuatia 1.2), multimile vagi sunt notate cu un simbol multime cu imprimare (subliniere) tilda; deci, de exemplu A va fi multimea vaga A. Aceasta functie aplica elementele unei multimi vagi A unei valori reale din intervalul (0,1). Daca un element din univers, x, este un membru al multimii vagi A, atunci aceasta aplicatie este data de ecuatia 1.2 sau m_a (x) E[0,l]. Aceasta aplicatie este aratata in figura 2.14 pentru o multime vaga tipica.

O conventie de notatie pentru multimile vagi cand universul prelegerii, X, este diferit si finit, este dupa cum urmeaza pentru multimea vaga A:

Cand universul, X, este continuu si finit, multimea vaga A este notata:

In ambele notatii, bara orizontala nu este un coeficient ci mai degraba un delimitator. Numaratorul in fiecare termen este valoarea (grad) de apartenenta in multimea A asociata elementului universului indicat in numitor. In prima notatie, simbolul suma nu este pentru suma algebrica ci mai degraba denota colectia sau acumularea fiecarui element , de aici incolo, semnele "+" in prima notatie nu sunt adunarile algebrice ci reprezinta reuniunea functiei teoretice. In a doua notatie semnul integrala nu este integrala algebrica ci o notatie a reuniunii continue a functiei teoretice pentru variabile continue.

OPERATII CU MULTIMI VAGI

Se definesc trei multimi vagi A, B si C in universul X. Pentru un element dat x al universului, urmatoarele operatii ale functiei teoretice pentru operatiile multimii teoretice ale reuniunii, intersectiei si complementului sunt definite pentru A, B si C in X:

Reuniune         m_{A B} (x) = m _A (x) m_B (x)      (2.22)

Intersectie          m_{A B} (x) = m_A (x) m_B (x)     (2.23)

Complement    m _A (x) = 1 - m _A (x) (2.24)

Diagramele Venn pentru aceste operatii, extinse la considerarea multimilor vagi, sunt aratate in figurile 2.15-2.17.

Orice multime vaga A definita pe universul X este o submultime a acelui univers. De asemenea prin definitie, precum si cu multimile clare, valoarea (grad) de apartenenta a unui element x in multimea vida este 0 si valoare (grad) de apartenenta a unui element x in multimea intreaga X este 1.

Atentie!

Multimea vida si multimea intreaga nu sunt multimi vagi in acest context( fara imprimare tilda). Notatia potrivita pentru aceste idei este:

Colectia tuturor multimilor si submultimilor vagi din X este denumita multime putere vaga P(X). Ar trebui sa fie evident, bazat pe faptul ca toate multimile vagi se pot suprapune, ca numarul cardinal, n_P(x), al multimilor putere vaga este infinit:

Legile lui De Morgan pentru multimile clare sunt folosite si pentru multimile vagi asa cum indica aceste expresii:

A B = A B                         (2.26a)

A B = A B                          (2.26b)

Asa cum s-a enumerat mai inainte, toate celelalte operatii cu multimi clare sunt folosite si pentru multimile vagi, exceptie fac legile tertului exclus. Aceste doua legi nu sunt folosite pentru multimile vagi; de cand multimile vagi se pot suprapune, o multime si complementul sau pot de asemenea sa se suprapuna. Legile tertului exclus, extinse pentru multimile vagi, sunt exprimate de:

PROPRIETATI ALE MULTIMILOR VAGI

Multimile vagi urmeaza aceleasi proprietati ca si multimile clare. Din aceasta cauza si din cauza ca valorile de apartenenta ale unei multimi clare sunt submultimi ale intervalului [0,1], multimile clare pot fi gandite ca un caz special al multimilor vagi. Frecvent se folosesc proprietatile multimilor vagi care sunt prezentate mai jos.

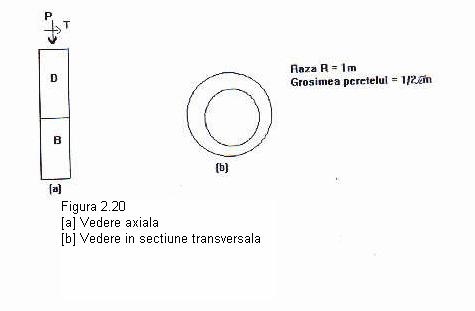
Exemplul 2.5. Se considera o raza simpla concava de aproximativ 1-m radius si grosimea peretelui (l/2p)m. Raza este construita prin asezarea unei

sectiuni elastice (ductile), D, a sectiunii transversale adecvate peste o sectiune fragila, B, dupa cum este aratat in figura 2.20. O forta de coborare P si un moment T sunt aplicate razei simultan . Din cauza dimensiunilor alese, presiunea nominala de marginire pe fiecare element de pe raza este T (pascali) si componenta verticala a presiunii pe raza este P (pascali ). De asemenea presupunem ca proprietatile esec ale ambelor B si D sunt necunoscute cu siguranta.

Definim multimea vaga A ca fiind regiunea in spatiul (P,T) pentru care

materialul D este "sigur", folosit ca un metric al functiei esec

m_A = f ([P² + 4 T ²]^1/2)

Similar, definim multimea B ca fiind regiunea in spatiul(P,T) pentru care materialul B este "sigur", folosit ca un metric al functiei esec

m_B = g (P - b T

unde b este un parametru presupus material.Functiile f si g vor fi,desigur, functii de apartenenta pe intervalul [0,1]. Specificarea lor exacta nu este importanta in acest punct. Ce este folositor, oricum prioritatea de a specifica functiile f si g, este discutarea operatiilor multime fundamentala in contextul acestei probleme. Aceasta discutie este rezumata mai jos:

aub este multumea incarcaturilor pentru care cineva se asteapta ca materialul B sau materialul D vor fi "sigure".

A B este multimea incarcaturilor pentru care cineva se asteapta ca ambele materiale B si D sunt "sigure".

_ _

3. A si B sunt multimi ale incarcaturilor pentru care materialul D si materialul B sunt nesigure.

4. A B este multimea incarcaturilor pentru care materialul ductil este sigur, dar materialul fragil este in pericol.

5. B | A este multimea incarcaturilor pentru care materialul fragil este sigur, dar materialul ductil este in pericol.

______ _ _

6. Legea lui De Morgan A B=A B- afirma ca incarcaturile care nu sunt sigure cu privire la ambele materiale reprezinta reuniunea acelora care sunt nesigure cu privire la materialul fragil cu acelea care sunt nesigure cu privire la materialul ductil.

7. Legea lui De Morgan A B A B- afirma ca incarcaturile care nu sunt sigure nici pentru materialul D nici pentru materialul B reprezinta intersectia acelora care nu sunt sigure pentru materialul D cu acelea care nu sunt sigure pentru materialul B.

8. Legea tertului exclus pentru multimi clare afirma ca incarcaturile care nu sunt evident "nesigure" sunt de aceea "sigure", dar cand exista neclaritate in nesiguranta lui A sau B exista incarcaturi care pot fi sigure si nesigure. Aceasta situatie este data realist de faptul ca esecul structural nu este binar in lumea reala.

Pentru a ilustra aceste idei numeric, sa luam doua multimi vagi:

Acum putem calcula mai multe din operatiile abia discutate (valoarea de apartenenta pentru elementul 1 in ambele multimi A si B este in mod implicit 0):

Exemplul 2.6

Una dintre operatiile de fabricatie cruciale asociate cu construirea tancului alimentat exterior cu combustibil pentru spatiul pendulator implica procesul de izolare prin pulverizare cu spuma (the spray-on foam insulation -SOFI), care combina doua preparate chimice critice intr-o arma pulverizatoare sub presiune ridicata, temperatura precisa si curs usor. Verificarea acestor parametrii in apropierea valorilor de punctul fixat este crucial pentru satisfacerea unui numar de liste cu nevoi importante. Listele cu nevoi constau din proprietati aerodinamice, mecanice, chimice si termodinamice.

Optimizarea procesului SOFI pentru a asigura un produs puternic in ciuda caracterelor variabile ale parametrilor din proces este o sarcina ce foloseste metodele proiectarii experimentului (design of experiment - DOE). Aceste metode constau in structurarea variabilelor procesului cheie intr-o multime de experimente conduse in laborator. Fiecarui element cheie ii sunt atribuite doua sau trei niveluri fixate si combinatii variate de elemente si niveluri sunt aranjate de obicei in concordanta cu o matrice definita in ordine. De exemplu fiecare linie a matricii defineste o combinatie utila a elementelor si nivelurilor. Procesul cheie si rezultatele (numite functie raspuns) sunt analizate statistic pentru a determina sensibilitatile relative ale elementelor procesului respectiv.

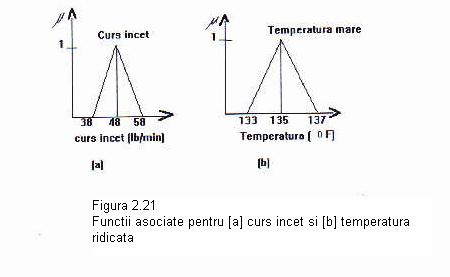
Unirea DOE-ului clar cu tehnicile caracterizarii vagi poate fi folosita la marirea experimentelor initiale. De exemplu in SOFI DOE ambele cursul si temperatura sunt critice. Nivelurile definite de matrice pot fi doar aproximate in realitate. Daca tintim o temperatura ridicata de 135°F, poate fi de la 133°F la 137°F.

Felul in care imprecizia sistemelor experimentale influenteaza variabilitatile functiei raspuns poate fi modelat prin folosirea metodelor multime vaga; de exemplu curs rapid (inalt) cu temperatura ridicata, curs incet cu temperatura mica. Exemplele sunt prezentate in figura 2.21 pentru un curs usor scazut si temperatura ridicata.

Sensibilitatea functiei raspuns la multimile vagi ale cursului si temperaturii pot fi evaluate folosind reuniunea, intersectia, complementul, diferenta, legile lui De Morgan si legile mijlocului exclus asa cum sunt legate de operatiile matematice asociate cu matricea definita al lui DOE. Sa dezvoltam reprezentarile grafice ale reuniunii si intersectiei.

Sa luam doua multimi pentru curs si respectiv temperatura:

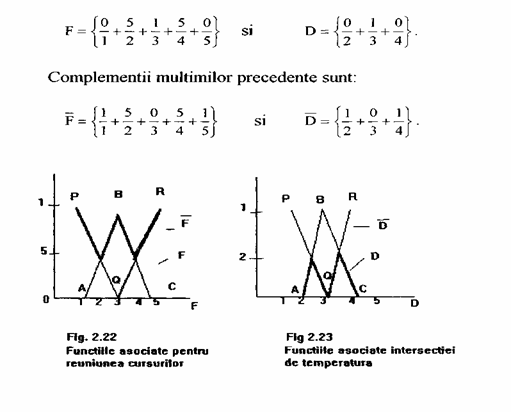
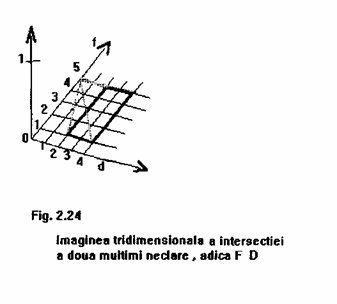
Reuniunea lui F si F este prezentata in figura 2.22 cu linii abrupte, unde functia de apartenenta a lui F este reprezentata de liniile AB si BC si functia de apartenenta a lui F este reprezentata de liniile PQ si QR. Intersectia lui D si D este aratata in figura 2.23 cu linii abrupte, unde functia de apartenenta a lui D este reprezentata de liniile AB si BC, functia de apartenenta a lui D este reprezentata de liniile PQ si QR. O imagine tridimensionala ar trebui sa fie construita cand luam reuniunea sau intersectia a doua multimi din doua universuri diferite. De exemplu, intersectia lui F si D este data in figura 2.24. Ideea de a combina functii de apartenenta din doua universuri diferite intr-o forma ortogonala, prezentata in figura 2.24 va fi aratata in capitolul 3 ca fiind asociata cu ceea ce sunt numite multimi vagi neintercalate.

MULTIMI CA PUNCTE IN SPATII CU MAI MULTE DIMENSIUNI

Este un analog geometric interesant pentru a ilustra ideea de multime de apartenenta [Kosko, 1992]. Pana acum a descris o multime vaga A pe un univers. Pentru un univers cu doar un element, functia de apartenenta este definita pe intervalul unitate [0,1]; pentru un univers cu doua elemente, functia de apartenenta este definita pe unitatea patrat, si pentru un univers cu trei elemente, functia de apartenenta este definita pe unitatea cub. Toate aceste situatii sunt prezentate in figura 2.25. Pentru un univers cu n elemente definim apartenenta pe o unitate cu spatii cu mai multe dimensiuni Iⁿ=[0,l]".

Punctele extreme pe intervalul unitate in figura 2.25a si varfurile unitatii patrat si varfurile unitatii cub in figurile 2.25b si 2.25c reprezinta posibilele submultimi clare sau colectii de elemente din univers in fiecare figura. Aceasta colectie de submultimi posibile clare de elemente dintr-un univers constituie multimea putere a universului. De exemplu in figura 2.25c universul cuprinde trei elemente, X = . Punctul (0,0,1) reprezinta submultimea clara in 3-spatiu, unde x₁ si x₂ nu au apartenenta si elementul x₃ are apartenenta plina, de exemplu submultimea punctul (1,1,0)este submultimea clara unde x₁ si x₂ au apartenenta plina si elementul x₃ nu are apartenenta, de exemplu submultimea ; si asa mai departe pentru celelalte sase varfuri in figura 2.25c. In general sunt 2ⁿ submultimi in multimea putere a unui univers cu n elemente; geometric acest univers este reprezentat de un cub in n-spatiu, unde varfurile 2ⁿ reprezinta colectia multimilor ce constitute multimea putere. Doua puncte in diagrame poarta simboluri speciale, asa cum este ilustrat in figura 2.25c. In aceasta figura punctul (1,1,1) unde toate elementele din univers au apartenenta plina, este numit multimea intreaga X si punctul (0,0,0) unde toate elementele din univers nu au apartenenta este numit multimea vida 0.

Centrii de greutate ai fiecaror diagrame in Figura 2.25 reprezinta punctele singure unde valoarea de apartenenta pentru fiecare element din univers este egala cu 1. De exemplu, punctul (1/2,1/2) in figura 2.25 b este punctul din mijlocul patratului. Acest punct de mijloc in fiecare din cele trei figuri este un punct special - este multimea "fuzzitatii" maxime. O valoare de apartenenta a lui 1/2 arata ca elementul apartine multimii vagi in aceeasi masura in care nu apartine - ceea ce inseamna ca ocupa apatenenta in multimea vaga si in complementul ei. In sens geometric, acest punct este locatia in spatiul care este cel mai indepartat de oricare dintre varfuri si inca echidistant de fiecare din ele. De fapt, toate punctele interioare varfurilor spatiilor reprezentate in figura 2.25 reprezinta multimi vagi unde valoarea de apartenenta a fiecarei variabile este un numar cuprins intre 0 si 1. De exemplu in figura 2.25b punctul (1/4,3/4) reprezinta o multime vaga unde variabila x₁ are un grad de apartenenta de 0,25 in multime si variabila x₂ are un grad de apartenenta de 0,75 in multime. Este evident din cercetarea diagramelor ca, desi numarul submultimilor in multimea putere este enumerat de 2ⁿ varfuri, numarul multimilor vagi din univers este infinit, asa cum sunt reprezentate de numarul infinit al punctelor din interiorul fiecarui spatiu.

In cele din urma, poate fi vazut ca varfurile cubului in figura 2.25c sunt coordonatele identice gasite in multimea valoare V} expusa in Exercitiul 2.4 al acestui capitol.

Rezumat

In acest capitol am extins definitiile fundamentale, proprietatile multimilor clare si vagi si operatiile cu multimi clare si vagi. A fost aratat ca singurele axiome fundamentale care nu sunt comune ambelor multimi clare si vagi sunt cele doua legi ale mijlocului exclus. Toate celelale operatii sunt comune celor doua multimi clare si vagi. Pentru multe situatii in discutie, legile tertului exclus prezinta ceva dintr-o constrangere (a se vedea Capitolul 15, Epilog). Exceptand diferenta multimii de apartenenta ca fiind o idee infinit evaluata spre deosebire de o cantitate binar evaluata, multimile vagi sunt manuite si tratate in aceeasi forma matematica precum multimile clare. Din nou, ideea ca multimile clare sunt forme speciale ale multimilor vagi a fost ilustrata grafic in sectiune de multimi ca puncte, unde multimile clare sunt reprezentate de varfurile unui spatiu cu mai multe dimensiuni. Toate celelalte puncte din spatiul cu mai multe dimensiuni, sau de-a lungul marginilor sale, sunt analoguri grafice la o multime vaga.

Sisteme de control vagi (Fuzzy control systems)

"Diferenta dintre stiinta si subiectele vagi este ca stiinta cere,se bazeaza pe argumente, in timp ce aceste subiecte vagi cer numai invatatura."

Robert Heinlein

Time enough for love, 1973

Un sistem de control este un ansamblu de componente fizice construit pentru a modifica, a regula, sau pentru a da comenzi, printr-o actiune de control altui sistem fizic, asa ca acesta expune, manifesta caracteristici dorite sigure sau un comportament dorit. Sistemele de control sunt de doua tipuri: sisteme de control inel sau cerc deschis (open-loop) in care controlul actiunii este independent de productia sistemului fizic si sisteme de control inel sau cerc inchis (stiut si sub denumirea de sisteme de control feedback), in care actiunea de control depinde de productia sistemului fizic. Exemple de sisteme de control inel-deschis sunt: un aparat de prajit painea, in care cantitatea de caldura e fixat de om si o masina de spalat automata, in care comenzile de control pentru temperatura apei, timpul ciclu de invartire si tot asa sunt comandate de om. In amandoua cazuri, actiunile de control nu sunt o functie de productie a masinii de prajit paine sau masinii de spalat. Exemple de control feedback sunt: un termostat de camera, care sesizeaza temperatura camerei si activeaza o unitate de caldura sau de racoare cand a ajuns la un prag sigur de caldura, si un mecanism autopilot, care face un curs automatic de corectari pentru un avion cand are deviatii mari sau de altitudine din cauza unor valori, lucruri ordonate sigur sunt sesizate de instrumentele din bordul avionului.

Pentru a controla orice variabila fizica, noi trebuie prima data sa o masuram, sa o apreciem. Sistemul pentru masurat semnalul de control este numit senzor. Sistemul fizic de sub control este numit planta. Intr-­un sistem de control inel inchis, semnale puternice sigure a sistemului (numite inputs) sunt determinate de raspunsurile sistemului (numite outputs). Pentru a obtine raspunsuri si caracteristici satisfacatoare pentru sistemul de control inel inchis este necesar a conecta un sistem suplimentar, cunoscut ca compensator, sau controlor, in inel. Forma generala a sistemului de control inel inchis este ilustrat in Fig.l [Phillip and Harbor, 1988].

Sistemele de control sunt cateodata divizate in doua clase. Daca obiectul, scopul, sistemului de control este pentru a mentine o variabila fizica la o anumita valoare constanta intr-un mediu de tulburatii, sistemul e numit tip regulat de control, sau regulator. Controlul temperaturii camerei si autopilotul sunt exemple de regulatori. A doua clasa de sisteme de control sunt tracking (drum, pista) controlers. ln aceasta schema de control,o variabila fizica e ordonata sa urmeze cateva functii prestabilite in timp. Un exmplu de acest tip de sistem este un sistem de aterizare al unui avion, in care avionul urmeaza o "rampa" spre punctul de aterizare dorit.

Problema controlului este satbilita cum urmeaza [Phillips and Harbor, 1988]. Productia, sau raspunsul sistemului aflat sub control (i.e. planta) este ajustata dupa dorinta semnalului de eroare. Semnalul de eroare este diferenta dintre raspunsul actual al plantei,masurat de sistemul senzor, si raspunsul dorit, specificat de inputul initial, de referinta.

In urmatoarea sectiune, noi obtinem diferite forme de modele matematice ordinare, raspandite, descriind un sistem de control inel inchis.

Recapitulare a teoriei sistemelor de control

Un model matematic ce descrie o varietate larga de sisteme fizice este o ecuatie diferentiala ordinara de rang n de tipul [Vidyasagar,1978]

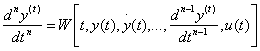
unde t este parametru timp,u( ) este functia input, w[ ] este o functie nelineara generala, si y( ) este sistemul output sau raspunsul functiei. Daca noi definim functiile auxiliare

atunci ecuatia unica de rang n (13.1) poate fi echivalenta exprimata cu un sistem de n ecuatii de prim rang:            

x₁(t)=x₂(t)

x₂(t)=x₃(t)

.

.

x_n-1(t)=x_n(t)

x_n(t)=w[t,x,(t),x₂(t),.,x_n(t),u(t)]

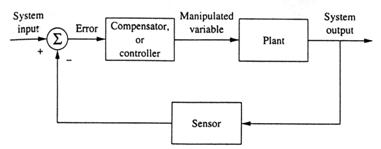
Fig.13.1 Un sistem de control inel inchis.

In final, daca noi definim n functii-vector cu valori x( ) si f( ) ca

(13.4) x(t)=[x₁(t),x₂(t),...,x_n(t)]^T

(13.5) f(t,x,u)=[x₂,x₃,...,x_n,w(t,x₁,...,x_n,u)]^T

unde x(t) este sistemul stabilit vector la timpul t (T este vectorul standard transpus), atunci primele n ecuatii de prim rang (13.3) pot fi combinate intr-o ecuatie diferentiala de prim rang tip vector:

x(t)=f[t,x(t),u(t)]

si rezultatul y(t) este dat din ecuatia (13.2) astfel

(13.7) y(t)=[1,0,...,0]x(t)

Similar un sistem cu p inputuri, m rezultate si n stabilite vor fi descrise, in general, folosind functiile vector cu valorile f ] si g[ ] astfel

x(t)=f[t,x(t),u(t)]

(13.9) y(t)=g[t,x(t),u(t)]

unde u(t) si y(t), vectorii, sunt definiti astfel

(13.10) u(t)=[u₁(t),u₂(t),...,u_p(t)]^T

(13.11) y(t)=[y₁(t),y₂(t),...,y_m(t)]^T

si sunt un vector de intrare si respectiv un vector de iesire.

Vectorul cu variabile stabilite x(t) este definit de ecuatia (13.4). Descrierile sistemelor fizice bazate pe ecuatia (13.8) si (13.9) sunt cunoscute ca reprezentantii multimii starilor (state-space) si x₁,x₂,...,x_n sunt cunoscute ca variabilele de rang ale sistemului. In cazul sistemelor contin invariante nelineare, ecuatiile (13.8) si (13.9) devin:

x(t)=f[x(t),u(t)]

(13.13) y(t)=g[x(t),u(t)]

si pentru sistemul de invariante liniare se va reduce catre urmatoarea forma:

x(t)=A·x(t)+B·u(t)

y(t)=C·x(t)+D·u(t)

unde constantele A, B, C si D sunt cunoscute ca matrici sistem.

Un sistem nelinear cu o unica data de intrare si o unica data de iesire de prim rang este descrisa folosind o ecuatie timp-discret ca

(13.16) x_k+1=f(x_k,u_k)

unde x_k+1, x_k sunt valorile rangului la momentele k si k+1, si u_k este data de intrare la momentul k. Un sistem cu o unica data de intrare si o unica data de iesire la n comenzi poate fi aratata in urmatoarea forma:

(13.17) y_k+n=f(y_k,y_k+1,...,y_k+n-1,u_k)

si pentru un sistem discret cu multiple date de intrare si o unica data de iesire la n comenzi:

(13.18) y(k+n)=f[y(k),y(k+1),...,y(k+n-1),u₁(k),u₂(k),...,u_p(k)]

Ecuatiile (13.14), (13.15) si (13.17) sunt ilustrate in problema cu pendulul inversat care va fi abordat in exemplu 13.2.

Problema de identificare a sistemului

Problema generala de identificare a unui sistem fizic bazat pe dimensiunile datelor de intrare, de iesire, si variabilele rang sunt definite ca functiile obtinute f si g in cazul unui sistem nelinear, si matriciile sistem A, B, C si D in cazul unui sistem linear. Exista algoritmi care converg, conduc, adaptabil la acesti parametri sistem bazate pe date numerice luate din variabile de intrare si de iesire [Ljung and Soderstrom,1983]. Sistemele vagi si paradigmele de retea neuronale artificiale sunt doua discipline dezvoltate pentru probleme de identificare a sistemelor nelineare.

Problema model a sistemelor de control

Problema generala a modelului sistemului de control feedback este definita ca obtinand o functie vector nelineara generala h( ), definita cum urmeaza [Vadiu, 1993].

(13.19) u(t)=h[t,x(t),r(t)]

unde u(t) este data de intrare catre planta sau procese, r(t) este data de intrare de referinta si x(t) este vectorul rang. Legea de control feedback h are scopul de a stabiliza sistemul de control feedback si rezulta intr-o realizare satisfacatoare. In cazul unui sistem timp-invariant cu un regulator, controlor, unde data de intrare de referinta este o constanta "setpoint" majoritatea vasta de controlori sunt bazati pe modelele generale date in ecuatia (13.20) si (13.21), care este, atat "full state feedback" sau "output feedback", cunoscut ca:

(13.20) u(t)=h[x(t)]

(13.21) u(t)=h[y(t),y,∫ydt]

In cazul sistemului simplu cu unica data de intrare si unica data de iesire si a unui regulator tip controlor,fimctia h ia una dintre urmatoarele forme:

(13.22) u(t)=K_p·e(t)

pentru un controlor proportional, sau P,

(13.23) u(t)=K_p · e(t)+K_I · ∫e(t)dt

pentru un controlor proportional-plus-integral, sau PI;

(13.24) u(t)=K_p· e(t)+K_D· ė(t)

pentru un controlor "proportional-plus-derivative", sau PD, (vezi exemplu 13.10 pentru PD controlor);

(13.25) u(t)=K_p· e(t)+K_l · ∫e(t)dt+K_D · e(t)

pentru un controlor "proportional-plus-derivative-plus-integral", sau PID, unde e(t),e(t) si ∫e(t)dt sunt eroare de iesire, eroare de derivare, si eroare de integrare, respectiv, si

(13.26) u(t)= -[k₁ · x₁(t)+k₂ · x₂(t)+...+k_n · x_n(t)]

pentru un controlor "full-state-feedback".

Problema modelului sistemului de control este definit ca obtinand functia nelineara generala h( ) in cazul sistemelor nelineare; coeficientii K_p, K_I, si K_D in cazul sistemelor "output-feedback" si coeficientii l₁, l₂, ..., l_n in cazul politicii de control "full state-feedback" pentru sisteme lineare. Functia h( ) in ecuatiile (13.20) si (13.21) descrie o suprafata nelineara generala care este cunoscuta ca o suprafata de control, sau de decizie, discutata in urmatoarea sectiune.

Suprafata de control (de decizie)

Conceptul de suprafata de control, sau suprafata de decizie, este centrala in metodologia sistemelor vagi de control [Vadiee, 1993]. In aceasta parte definim acest concept foarte important. Functia h definita in ecuatiile (13.19), (13.20) si (13.21), este in general, definita, ca hipersuprafata neliniara P intr-un spatiu n-dimensional. Pentru sisteme lineare cu "output-feedback" sau "state-feedback" in general este un hiperplan intr-un spatiu n-dimensional. Aceasta suprafata este cunoscuta ca suprafata de control, sau de decizie. Suprafata de control descrie dinamica controlorului si este in general o suprafata nelineara varianta timp-variabil. Datorita dinamiciilor nemodelate prezente in modelul unui controlor tehniciile ar trebui sa existe pentru reglare, ajustare, adaptabilitate si modificarea formei suprafetei de control.

Sistemele expert cu reguli logice de baza vagi folosesc o colectie de exprimari conditionale vagi derivate din cunostiinte experte construite pentru a aproxima si a construi suprafata de control [Mandami and Gains,l981; Kiszka et al., 1985; Sugeno, 1985]. Acest paradigm a modelului de sistem de control, este bazat pe rationament "interpolative" si aproximativ. Controlorii cu reguli de baza logici vagi sau sistemul de identificatori,sunt in general "paradigms-model-free".Sistemele experte cu reguli de baza logici vagi sunt aproximatii de functii nelineare universale, si fiecare functie nelineara (exemplu suprafata de control) cu n variabile independente si o variabila dependenta poate fi exprimata catre o oarecare precizie dorita. Alternativele retele neuronale artificiale sunt bazate pe o invatatura analogica si incearca sa invete suprafetele de decizie nelineare printr-o tehnica adaptabila si converginda bazata pe date numerice disponibile dimensiunilor datelor de intrare-iesire variabilelor sistemului si catorva criterii de realizare.

Etapele modelului sistemului de control

Pentru a obtine suprafata de control pentru un sistem dinamic complex "real-world" timp-variabil nelinear exista un numar de pasi folositi in modelarea unui controlor penru un sistem fizic complex care sunt urmatoarele:

Sistemele de scara larga sunt decentralizate si descompuse intr-o colectie de subsisteme decuplate.

Variatiile temporale ale dinamicii plantei sunt presupuse a fi "usor variind".

Dinamiciile plantei nelineare sunt local linearizate asupra unui set de "operating points" (vezi rotatia atributilor in exemplu 13.2).

Un set de variabile vectori, variabile de control, sau trasaturile de iesire este facut disponibil.

Un simplu P, PD, PID "output-feedback", sau controlor "state-feedback" este modelat pentru fiecare sistem decuplat. Controlorii sunt tip regulator si sunt suficienti de rapizi sa indeplineasca satisfacator sub situatii de control. Controlorii optimi ar putea sa se dovedeasca folositori.

In plusul nesigurantelor intoduse in primii 5 pasi, exista nesigurante cauzate de mediul inconjurator exterior. Modelul de control ar trebui sa fie facut cat mai apropiat posibil de cel mai optim bazat pe cunostintele inginerului de control in forma de date de observatie numerice intrare-iesire si informatii in legatura cu dinamiciile plantei si cu mediul inconjurator, exterior.

Un sistem de control superior, cat si un mecanic expert automatic sau uman, formeaza un nod de control "aditional feedback" pentru a regla si a ajusta parametrii controlorului, pentru a compensa efectele variatiilor cauzate de dinamica nemodelatoare.

Atribuirea in modelul sistemului de control vag

Un numar de atribuiri sunt implicite intr-un model de sistem de control vag. Sase atriburi de baza sunt facute de obicei oriunde o politica de control logic vag este selectata:

Planta este observabila si controlabila. Variabilele vector de intrare si de iesire sunt de obicei disponibile si masurate sau calculate.

Exista un corp de cunostinte cuprinse intr-un set de reguli lingvistice de productie experte, ratiune obisnuita inginereasca, intuitie, un set de date masurabile intrare-iesire sau un model analitic ce pot fi vagi si din orice regula pot fi extrase.

O solutie exista

Inginerul de control cauta o solutie "suficient de buna", nu necesar cea optima.

Vom modela un controlor cu cele mai bune cunostinte disponibile si cu un sir acceptabil de precizie.

Problemele de stabilitate si de optimizare sunt inca probleme deschise in modelul de control vag. Urmatoare parte abordeaza procedura de a obtine suprafata de control, h( ) din aproximatiile bazate pe o colectie de reguli daca-atunci vagi ce descriu dinamica controlorului. Modelele experte cu reguli de baza vagi pot fi folosite sa obtina aproximatii acceptabile pentru functiile f( ) si g( ) in cazul problemei de identificare de sistem .

Un sistem cu regulator de productie vaga este format din 4 structuri [Wein and Donnel, 1979]:

Un set de reguli ce reprezinta politicile si strategiile heuristice ale facatorului de decizii expert.

Un set de date de intrare directe,atribuite, imediat anterior deciziei actuale.

O metoda pentru a procesa orice actiune propusa exprimata in conformitate cu regulile exacte, dand date disponibile.

O metoda pentru generarea actiunilor promise si pentru determinare cand te opresti cautand pentru cel mai bun.

Datele de intrare, regulile, si actiunile de iesire, sau consecinta, sunt in general siruri vagi exprimate ca fimctii membri definite pe un spatiu potrivit. Metoda folosita pentru procesarea regulilor este cunoscuta ca ratiune aproximativa, sau ratiune "interpolative", si este de obicei reprezentat de compozitia relatiilor vagi aplicate unei ecuatii "relational" vagi.

Suprafata de control, care relateaza actiunea de control u( ) asupra vectorul masurat sau variabilele de iesire, este obtinuta folosind aceste patru structuri. Apoi este incercat la un numar finit de puncte, depinzand de rezolutiile cerute si o tabela de cautat este construita. Tabela de cautat astfel formata a putut fi realizata pe un cip de memorie read-only si va constitui un controlor fixat pentru planta.

Controlori logici vagi simplii

Controlorii logici vagi simplii din prima generatie (neadaptabili; i.e., cele patru structuri dinamice sunt fixati) pot fi in general infatisate de o diagrama bloc ca in fig. 13.2. Grupul de cunostinte de baza in fig. 13.2 contine cunostinte despre toate impartirile vagi de intrare si de iesire. Va include sirul de termeni si corespondenta functiilor membri definind variabilele de intrare la sistemul de reguli de baza vagi si variabilele de iesire sau actiunile de control, catre planta de sub control.

Etapele de a modela un sistem de control logic vag simplu sunt urmatoarele:

Identificarea variabilelor ( de intrare, vectori,si de iesire), ale plantei

Impartirea universului de discurs sau intervalul construit "spanned" de fiecare variabila intr-un numar de subsiruri vagi, fixand fiecare o eticheta lingvistica (subsirurile includ toate elementele din universe)

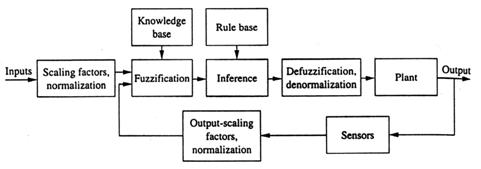
Fig. 13.2

O diagrama bloc sistem de control logic vag simplu.

Fixarea ori determinarea unei functii de apartenenta pentru fiecare subsir.

Fixarea relatiilor vagi dintre subsirurile vagi de intrare sau tip vectori pe de o parte si subsirurile vagi de iesire pe de alta parte, astfel formand regula de baza.

Alegeti un sir de factori apropiati pentru variabilele de intrare si de iesire pentru a normaliza variabilele catre intervalul [0, l ] sau [-1,1 ].

Fuzzify-carea datelor de intrare catre controlor.

Folositi rationamentul aproximativ vag pentru a interfera datele de iesire contribuite din fiecare regula.

Agregarea datelor de iesire vagi recomandate de fiecare regula.

Aplicati defuzzificarea pentru a forma o data de iesire fragila.

Intr-un controlor logic vag simplu neadaptabil metodologia folosita si rezultatele celor noua etape mentionate mai sus sunt fixate, pe cand intr-un controlor logic vag adaptabil, ele sunt adaptabil modificate bazate pe cateva legi de adaptare pentru a optimiza controlul.

Un sistem de control logic vag simplu are urmatoarele caracteristici:

Scara factorilor de intrare si de iesire fixati uniform.

Regula de baza a preciziei si unice impartiri cu reguli fixate si neintructive. Toate regulile au acelasi grad de siguranta si confidentialitate,capabile de unire.

Functii de apartenenta fixate.

Numar limitat de reguli, ce creste exponential cu numarul variabilelor de intrare.

"Fixed metaknowledge" incluzand metodologia pentru rationamentul apeoximativ, reguli de agregare si "output defuzzification".

Control al nivelului minim si nici o structura de reguli ierarhice.

Controlori logici vagi generali

Principalele elemente modelati intr-un sistem de control logic vag general (i.e., nesimplu) sunt urmatoarele [Lee, 1990]:

Strategiile fuzzificarii si interpretarea operatorului de fuzzzificare, sau fuzzificatorul.

Baza cunostiintelor:

a)     "Dicretization" normalizarea universului de discurs.

b)     Impartiriile vagi a spatiilor de intrare si iesire.

c)     Lipsa completarii ale impartiriilor

d)     Alegerea unor functii de apartenenta a unui sir vag primar.

Reguli de baza:

a)     Alegerea variabilelor vectori (de intrare) de procesare si a variabilelor de control (de iesire)

b)     Sursa derivatiei a regulilor de control vagi.

c)     Tipuri de reguli de control vagi.

d)     Consistenta, interactivitatea si lipsa completarii a regulilor de control vagi.

Luarea de decizii logice:

a)     Definirea implicarii vagi.

b)     Interpretarea elementului de conectare "si".

c)     Interpretarea elementului de conectare "sau".

d)     Mecanismul de deducere.

Strategiile de defuzzificare si interpretarea operatorului de defuzzificare ,defuzzificatorul.

Adaptarea sau schimbarea in oricare dintre cele cinci parametrii de model de dinainte creaza un sistem de control logic vag adaptabil. Daca toate cinci sunt fixate sistemul de control logic vag este simplu si neadaptabil.

Forme speciale ale modelelor sistemului de control logic vag

Cele mai multe modele de sistem de control logic vag pot fi exprimate in doua diferite forme: structurile de reguli de baza vagi si ecuatiile de legaturi vagi. Cele mai obisnuite structuri de reguli de baza vagi in sistemele de control vagi sunt cele cinci etape ale modelelor sistemelor de reguli de baza vagi descrise in capitolul 9 (ecuatiile 9.12-9.21).

Ecuatiile (13.27-13.32) demonstreaza ecuatiile de legatura vagi descriand un numar de modele de sistem de control vagi folosite obisnuite:

Consideram un sistem de prim rang discret cu data de intrare u, descris in forma de vector-spatiu. Baza modelului vag unui asemenea sistem are urmatoarea forma:

(13.27) x_k+1=x_k○u_k○R pentru k=1,2,.

unde R este relatia de transfer a sistemului vag, si unde o este compunerea

Un sistem de rang p discret cu o unica data de intrare u, descrisa intr-o forma de vector-spatiu, este data de ecuatia de sistem vag care urmeaza:

x_k+p=x_k○x_k+1○.○x_k+p-1○u_k+p-1○R pentru k=1,2,.

(13.29) y_k+p=x_k+p

unde y_k+p este unica data de iesire a sistemului.

Un sistem de rang al doilea cu "full state feedback" (vezi exemplu 13.1) este descrisa ca

u_k=x_k○x_k-1○R pentru k=1,2,.

y_k=x_k

Un sistem cu unica data de intrare si unica data de iesire de rang p discret cu "full state feedback" este reprezentata de urmatoarea ecuatie de legatura vaga (denumit dinamica Sugeno):

(13.32) u_k+p=y_k○y_k+1○.○y_k+p-1○R pentru k=1,2,.

Exemple de modele de sistem de control vag

Cele mai multe situatii de control sunt mult mai complexe decat noi putem avem de-a face matematic. In aceasta situatie controlul vag poate fi dezvoltat daca un grup de cunostinte despre procesul de control exista, si format intr-un numar de reguli vagi. De exmplu, presupunem ca data de iesire de proces industrial este dat in termenii de presiune. Noi putem calcula diferenta dintre presiunea dorita si presiunea rezultanta, numita eroare de presiune (e), si putem calcula diferenta dintre rata dorita de schimbarea presiunii, dp/dh, si rata de presiune actuala, rata erorii de presiune (e). Desi presupunand aceste cunostinte pot fi exprimate in forma regulilor daca-atunci ca de exemplu: Daca eroarea de presiune (e) este "pozitiva mare (PB)" sau "pozitiva medie (PM)" si daca rata erorii de presiune (e) este "negativa mica (NS)", atunci schimbarea caldurii de intrare este "negativa medie (NM).".

Variabilele lingvistice definand erorile de presiune, "PB" si "PM", si rata erorilor de presiune, "NS" si "NM", sunt vagi; dar dimensiunile presiunii si a ratei de presiune ca si valoarea de control pentru caldura (variabile de control) ultima aplicata sistemului sunt precise (fragile). Schema din fig. 13.3 arata aceasta idee. O data de intrare asupra procesului industrial(sistemului fizic) vine de la controlor. Sistemul fizic raspunde cu o data de iesire, ce este probat si masurat de niste dispozitive.

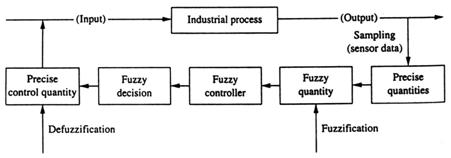
Fig.(13.3)

Situatie de control vag inel inchis tipic.

Daca data de iesire masurata este o cantitate fragila poate fi fuzzificata intr-un sir vag (vezi capitolul 4). Aceasta data de iesire vaga este apoi considerata ca data de intrare vaga intr-un controlor vag care consta in reguli lingvistice. Data de iesire a controlorului vag este atunci o alta serie de siruri vagi. De cand cele mai multe sisteme fizice nu putem interprata comande vagi (siruri vagi), data de iesire de control vag trebuie sa fie convertita in cantitati fragile folosind metode de defuzzificare (vezi capitolul 5). Aceste valori de iesire de control fragile defuzzzificate devin apoi valori de intrare catre sistemele fizice si intregul ciclu inel-inchis este repetat.

Exemplu 13.1. Pentru cateva uzine industriale un operator uman este cateodata mult mai eficient decat un controlor mecanic. Aceste strategii de control intuitive, ce furnizeaza o posibila metoda de a obtine informatii calitative, pot fi modelate de un controlor vag. Acest exemplu arata la un proces de presiune controlat de un controlor vag. Controlorul este format de un numar de reguli vagi, cum ar fi: Daca eroarea presiunii este "pozitiva mare" sau "pozitiva medie", si daca rata schimbarii in eroarea de presiune este "negativa mica", atunci schimbarea de intrare de caldura este "negativa medie". Acest exemplu este ilustrat in patru etape:

Etapa 1 Valoarea fixata pentru data de intrare vaga si variabilele de iesire.

Vom lasa eroarea (e) definita de opt variabile lingvistice, etichetate A₁, A₂, ..., A₈, impartite pe spatiul erorii [-e_m, +e_m], si rata erorii (e sau de/dt) definita de sapte variabile, etichetate B₁, B₂, ..., B₇ impartite pe spatiul erorii [-e_m, +e_m]. Vom normaliza aceste siruri catre acelasi interval [-a, +a] de

e₁=(a/e_m) · e

(13.34) e₁^·=(a/e_m^· ) · e^·

Pentru eroare, cele opt varibile vagi, A_I (I=1, 2, ..., 8), se vor conforma cu variabilele lingvistice, PB, PM, PS, PO, NO, NS, NM, NB. Pentru rata erorii, e, cele sapte variabile vagi, B_j (j=1, 2, ..., 7) se vor conforma variabilelor lingvistice PB, PM, PS, O, NS, NM, NB. Functiile de apartenenta pentru aceste cantitati vor fi in intervalul [-a,+a] unde a=b/a=6), si sunt aratate in Tabelele 13.1 si 13.2. (in tabele x=e si y=e).

Variabilele de iesire vagi, cantitatea de control (z),vor folosi sapte variabile vagi in universul normalizat, z=. Variabila de control va fi descrisa de cantitatile de control lingvistice vagi, C_k,(k=1, 2, ..., 7), care sunt impartite in universul de control. Tabela 13.3 este cantitatea de control normalizata, z, care este definita de sapte variabile lingvitice.

Etapa 2 Sumarul regulilor de control.

Conform experientei operatorului uman, regulile de control sunt de forma:

Daca e este A₁, si e este B₁, atunci z este C₁₁.

Daca e este A₁, si e este B₂, atunci z este C₁₂.

Daca e este A_I, si e este B_j, atunci z este C_ij.

Fiecare regula poate fi expusa intr-o relatie vaga, B. Folosind o astfel de cale va rezulta in variabilele lingvistice, C_ij, aratate ca intrari de control in Tabelul 13.4.

Tabelul 13.1

Functiile de apartenenta pentru eroarea (e)^*

X

AI

A1

PB

A2

PM

A3

PS

A4

P0

A5

N0

A6

NS

A7

NM

A8

NB

Etapa 3 Conversia dintre variabilele vagi si cantitatile precise.

Din datele de iesire ale sistemului noi putem folosi un instrument de a masura eroarea (e) si de a calcula rata erorii (e), amandoua fiid numere precise. O procedura de defuzzificare standard pentru a dezvolta functiile membre, ca de exemplu principiul de membru maximum (vezi capitolul 5), poate fi folosit de a lua cantitatile vagi corespunzatoare (Ai,Bi). Trimitand A si B obtinute de la datele de iesire ale sistemului catre controlorul vag va da o variabila de actiune vaga C (reguli de control), fiind discutata in etapa 2.

Tabela 13.2 *

Functiile de apartenenta pentru rata de eroare(de/dt)

Y

Bj

B1

PB

B2

PM

B3

PS

B4

B5

NS

B6

NM

B7

NB

Tabela 13.3 *

Functiile de apartenenta pentru cantitatea de control (z)

Z

Ck

C1

PB

C2

PM

C3

PS

C4

C5

NS

C6

NM

C7

NB

Dar inainte de a implementa controlul, noi trebuie sa introducem cantitatea de control exacta z in sistem. Avem nevoie de alta conversie de la C la Z. Aceasta poate fi facuta de un principiu membru maxim, sau de o metoda medie impovratoare (vezi capitolul 5).

Etapa 4 Dezvoltarea tabelului de control

Cand procedurile din etapa 3 sunt folosite pentru toti e si pentru toti e, vom obtine un tabel de control, aratat in tabelul 13.5. Acest tabel contine acum cantitati numerice exacte pentru folosirea de catre sisteme industriale hardware. Daca valorile in tabelul 13.5 sunt conspirate ele reprezinta suprafata de control. Figura 13.4 este suprafata de control pentru acest exemplu si figura 13.5 va fi suprafata de control pentru acest exemplu daca ar fi fost dirijat folosind numai siruri fragile si operatii (pentru cazul fragil, valorile in tabelul 13.5 va fi diferit). Volumul sub suprafata de control este proportional cu cantitatea energiei data de controlor. Poate fi aratat ca suprafata de control vag (fig. 13.4) va fixa de fapt dedesubtul suprafetei de control fragila (fig 13.5), indicand ca controlul vag da mai putina energie decat controlul fragil.

Tabelul 13.4

Reguli de control (tabelul FAM)  

A_I

	NB
Bj
PB	PB	PM	NB	NB	NB	NB
PM	PB	PM	NM	NM	NS	NM
PS	PB	PM	NS	NS	NS	NS	NM	NB
	PB	PM	PS			NS	NM	NB
NS	PB	PM	PS	PS	PS	PS	NM	NB
NM			PS	PS	PM	PM	NM	NB
NB			PB	PB	PB	PB	NM	NB

Tabelul 13. 15

Actiuni de control

y

X

Metodele de contol vag,ca si acesta, au fost folosite pentru cateva sisteme industriale si au realizat eficienta semnificativa. [Mandani, 1974; Pappas si Mandani, 1976].

In exemplul anterior noi n-am dirijat o simulare a unui proces de control pentru ca nu avem un model pentru controlor. Dezvoltarea suprafetei de control este simplu derivat din regulile de control si functiile membre asociate. Dupa ce suprafata de control este dezvoltata,o simulare poate fi dirijata daca un model

matematic sau lingvistic (reguli de baza) a procesului de control disponibil.

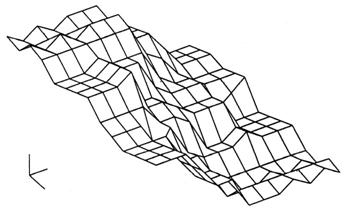
Fig, 13.4

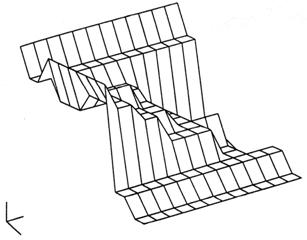
Fig 13.5

Probleme de control vagi clasice:

Pendulul inversat

Figura 13.6 arata sistemul pendulului inversat clasic, care a fost un caz intersant in teoria controlorului pentru multi ani.

Exemplu 13.2. Vrem sa modelam si sa analizam un controlor vag pentru versiunea simplificata a sistemului pendulului inversat din fig 13.6. Ecuatia diferentiala descriind sistemul este data mai jos [Kailath, 1980; Craig, 1986]:

(13.35) -ml²d²θ/dt²+(mlg)sin(θ)= τ =u(t)

unde m este masa polului fixat la varful pendului, l este lungimea pendulului, θ este unghiul de deviere fata de verticala in directia acelor ceasornice, τ=u(t) este momentul aplicat polului in directia inversa arcelor ceasornice (u(t) este actiunea de control), t este timpul si g este constanta de acceleratie gravitationala.

Presupunand x₁=θ si x₂=dθ/dt a de variabile vectori,reprezentarea vector-spatiu pentru sisteme nelineare definite de ecuatia (13.35) este data de dx/dt=x₂, dx₂/dt=(g/l)sin(x₁)-(1/ml²)u(t).

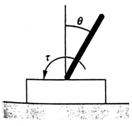
Figura 13.6

Este cunoscut ca pentru fiecare rotatie mica, sau θ, avem sin(θ)= θ, unde θ este masurata in radiani. Aceasta relatie e folosita pentru a lineariza ecuatiile vector-spatiu nelineare, si obtinem:

dx₁/dt=x₂

dx₂/dt=(g/l)x₁-(1/ml²)u(t)

Daca x₁ este masurat in grade si x₂ in grade si secunde, alegand l=g si m=180/(π*g²), ecuatiile vector­spatiu linearizate si timp-discret pot fi reprezentate ca ecuatii diferentiale tip matrice,

x₁(k+1)=x₁(k)+x₂(k)

x₂(k+1)=x₁(k)+x₂(k)-u(k)

Pentru aceasta problema vom dirija universul de discutat pentru doua variabile sa fie -2° ≤ x₁ ≤ 2° si -5dps ≤ x₂ ≤ 5dps (dps=grade la/pe secunda).

Etana 1 Prima data vrem sa construim trei functii de apartenenta pentru x, pe universut lui, acesta este, pentru valori pozitive (P), zero (Z), si negative (N), aratate in fig. 13.7. Apoi construim trei functii de apartenenta pentru x₂ pe universul lui,pentru valori pozitive (P), zero (Z), si negative (N), aratate in fig. 13.8.

Etapa 2 Pentru a imparti spatiul de control (de iesire), vom construi cinci functii de apartenenta pentru u(k) pe universul lui, care este -24 ≤ u(k) ≤ 24, ca in fig.13.9 (Aceasta figura are sapte impartiri dar noi vom folosi numai cinci pentru aceasta problema).

Etapa 3 Vom construi apoi noua reguli (chiar daca nu vom avea nevoie de atatea reguli) intr-o tabela 3x3 FAM, Tabelul 13.6, pentru acest sistem, care va implica θ si θ^· pentru a stabiliza sistemul pendulului "inverted". Intrarile in acest tabel sunt actiunile de control, u(k).

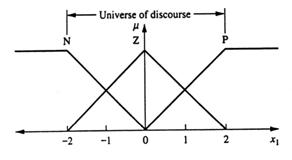
Figura 13.7

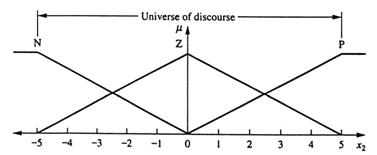
Figura 13.8

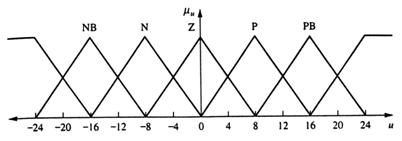
Figure 13.9

Etapa 4 Folosind regulile exprimate in tabelul 13.6, vom dirija acum o simulare a acestei probleme de control. ln dirijarea simularii vom folosi metoda grafica prezentata in capitolul 8 pentru a ghida operatiile vagi. Pentru a incepe simularea vom folosi urmatoarele conditii initiale fragile: x₁(0)=1° si x₂(0)= -4dps. Apoi vom ghida patru cicluri de simulare folosind matricea ecuatiilor diferentiale, de dinainte, pentru etapele discrete 0 ≤ k ≤ 3. Fiecare ciclu de simulare vor rezulta in functiile de apartenenta pentru actiunea de control, u(k). Vom defuzzzifica functia de apartenenta pentru actiunea de control folosind metoda centrului de greutate si apoi vom folosi ecuatiile diferentiale recursive pentru a rezolva pentru valorile noi ale lui x₁ si x₂. Fiecare ciclu de simulare dupa k=0 va incepe cu valorile anterioare ale lui x₁ si x₂ ca conditiile de intrare urmatoruiui ciclu ale ecuatiilor diferentiale recursive. Figurile 13.10 si 13.11 arata conditiile initiale pentru x₁ si respectiv x₂.

Din tabelul FAM (tabelul 13.6):

Daca (x₁=P) si (x₂=7) atunci (u=P) min (0,5; 0,2) = 0,2(P)

Daca (x₁=P) si (x₂=N) atunci (u=Z) min (0,5; 0,8) = 0,5(Z)

Daca (x₁=Z) si (x₂=N) atunci (u=N) min (0,5; 0,8) = 0,5(N).

Figura 13.12 arata unirea consecintelor vagi trunchiate pentru variabila de control, u. Forma finala, cu valoarea de control defuzzificata este aratata in fig.13.13.

Tabelul 13.6

Tabelul FAM

X2 X1	P	Z	N
P	PB	P	Z
Z	P	Z	N
N	Z	N	NB

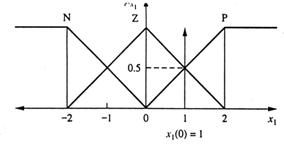
Fig 13.10

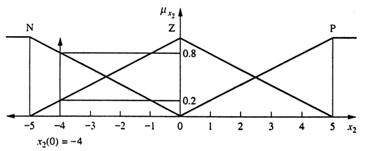
Fig 13.11

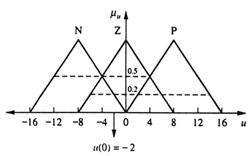
Fig 13.12

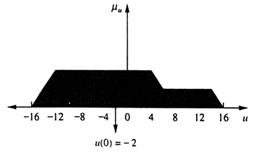
Fig 13.13

Am completat primul ciclu de simulare. Acum luam valoarea variabilei de control defuzzificata (i.e., u=-2) si,folosind ecuatiile sistemului, gasim conditiile initiale pentru urmatoarea iteratie

x₁=x₁(0)+x₂(0)=1-4= -3

x₂(1)=x₁(0)+x₂(0)=1-4-(-2)= -1

Din aceasta vom lua conditiile initiale pentru al doilea ciclu unde x₁(1)=-3 si x₂(1)=-1, care sunt aratate grafic in figura 13.14 si 13.15.

Din tabelul FAM (tabelul 13.6):

Daca (x₁=N) si (x₂=N) atunci (u=NB) min (1; 0,2)=0,2(NB)

Daca (x₁=N) si (x₂=Z) atunci (u=N) min (1; 0,8)=0,8(N)

Uniunea consecintelor vagi si datele de iesire defuzzificata rezultante sunt aratate in fig.13.16. Valoarea defuzzificata este u=-9,6.

Acum folosim u=-9,6 pentru a gasi conditiile initiale pentru al treilea cycle de iteratie:

x₁(2)=x₁(1)+x₂(1)=-3-1=-4

x₂(2)=x(1)+x₂(1)-u(1)=-3-1-(-9,6)=5,6

Astfel luam conditiile initiale x₁(2)=-4 si x₂(2)=5,6, care sunt aratate grafic in figura 13.17 si respectiv 13.18. Din tabelul FAM (tabelul 13.6).

Daca (x=N) si (x₂=P), atunci (u=Z) min (1; 1)=1(Z).

Consecintele rezultante si variabila de control defuzzificata, u(z)=0,0, sunt aratate in figura 13.19. Pentru urmatoarea iteratie,

x₁(3)=x₁(2)+x₂(2)=-4+5,6=1,6

x₂(3)=x₁(2) +x₂(2)-u(2)=-4+5,6-(0,0)=1,6.

Conditiile initiale x₁(3)=1,6 si x₂(3)=1,6 sunt aratate grafic in figurile 13.20 si respectiv 13.21. Din tabelul 13.6 avem:

Daca (x₁=Z) si (x₂=P), atunci (u=P) min (0,25; 0,3)=0,3(P)

Daca (x₁=Z) si (x₂=Z), atunci (u=Z) min (0,25; 0,7)=0,25(Z)

Daca (x₁=P) si (x₂=P), atunci (u=PB) min (0,75; 0,3)=0,3(PB)

Daca (x₁=P) si (x₂=Z), atunci (u=PB) min (0,75; 0,7)=0,7(P)

Aceste conditii sunt aratate in figura 13.22, si valoarea defuzzzificata este u=5,38.

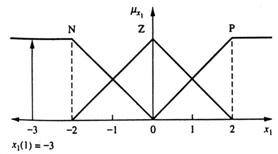
Fig 13.14

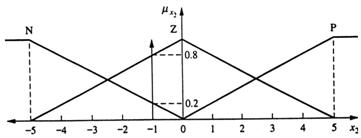
Fig 13.15

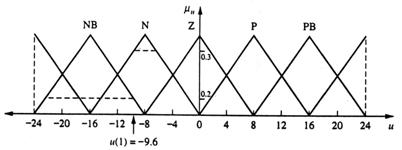
Fig 13.16

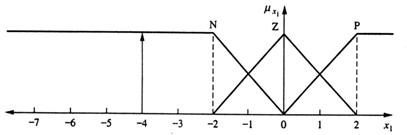
Fig 13.17

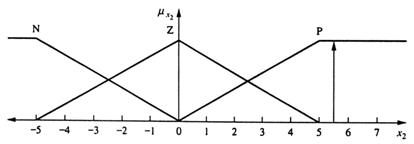
Fig 13.18

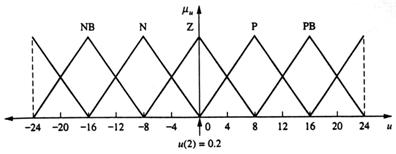
Fig 13.19

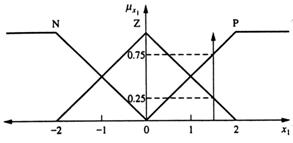
Fig 13.20

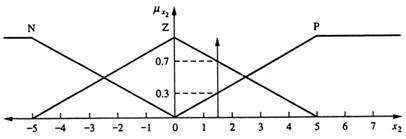
Fig 13.21

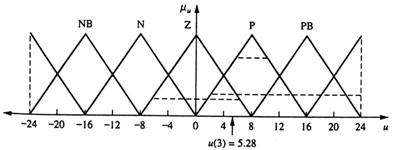
Fig 13.22

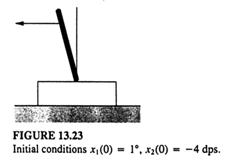
Fig 13.23

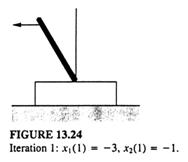
Fig 13.24

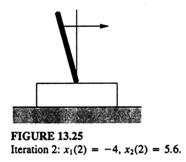
Fig 13.25

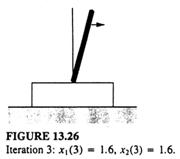
Fig 13.26

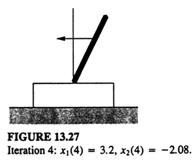
Fig 13.27

Ca inainte, vom folosi u=5,28 pentru a gasi conditiile initiale pentru urmatoarea iteratie,

x₁(4)=x₁(3)+x₂(3)=1,6+1,6=3,2

x₂(4)=x₁(3)+x₂(3)-u(3)=1,6+1,6-(5,28)=-2,08.

Astfel, avem conditiile initiale x₁(4)=3,2 si x₂(4)=1,12 (fara figura). Terminam simularea la acest punct.

Etapa 5 Acum enuntam, povestim cele patru cicluri de simulare pentru x₁, x₂ si u(k). In figurile de la 13.23 la 13.27, lungimea si directia sagetei sunt proportionale cu viteza unghiulara si respectiv arata directia miscarii pendulului.

Problema de control a aterizarii avionului

Urmatorul exemplu arata flexibilitatea si precizia rezonabila pentru alte aplicatii in control vag.

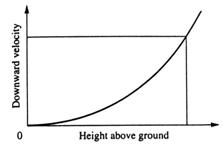
Fig. 13.28.

Exemplu 13.3 Vom ghida o simulare a coborarii finale si modul de aterizare a unui avion. Profilul dorit este aratat in fig.13.28. Viteza de aterizare dorita este proportionala cu scara inaltimii. Astfel, la altitudini inalte, este dorita o viteza de coborare mare. La inaltimi mai mici, viteza de coborare e din ce in ce mai mica. La limita, de la cea mai mare inaltime catre cea mai mica, viteza de coborare devine zero. In acest fel, avionul va cobora de la altitudini prompt dar va atinge solul foarte usor pentru a evita avarierea.

Cele doua variabile vector pentru aceasta simulare va fi inaltimea fata de pamant, h, si viteza verticala a avionului, v. fig (13.29). Datele de iesire de control vor fi fortate, cand aplicata avionului, va schimba inaltimea lui,h,si viteza, v? Ecuatiile de control diferentiale sunt derivate liber cum urmeaza. Vezi fig.13.30. Masa m deplasanduse cu viteza v are impulsul p=mv. Daca nici o forta externa nu este aplicata masa va continua in aceeasi directie la aceeasi viteza,v. Daca o forta f este aplicata dupa un interval de timp, va rezulta o schimbare in viteza ∆v=f ∆t/m.

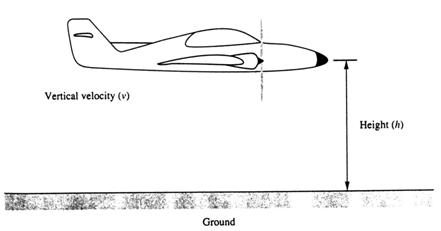
Fig 13.29.

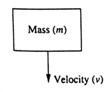
Fig 13.30.

Daca avem ∆t=10(sec) si m=1,0(lb-sec²/ft), obtinem ∆v=f(lb), sau schimbarea vitezei este proportional cu fortele aplicate.

In rotatia diferentiala avem

v_i+1=v_i+f_i

h_i+1=h_i+vi(1)

unde v_i+1 este noua viteza, v_I este viteza veche, h_i+1 este inaltimea noua si h_I este inaltimea veche. Aceste doua "ecuatii de control" definesc valoarea noua variabilelor vector v si h ca raspunsuri de a controla datele de intrare si valorile variabilelor vectori anterioare. Acum, urmarind aceeasi procedura ca in exemplu 13.2, etapa 1, construim functiile de apartenenta pentru inaltime, h, viteza verticala, v, si forta de control, f.

Etapa I Definirea functiilor de apartenenta pentru variabilele vector aratate in tabelele 13.7 si 13.8 si figurile 13.31 si 13.32.

Etana 2 Definirea unei functii de apartenenta pentru data de iesire de control, aratate in tabelul 13.9 si figura 13.33.

Etapa 3 Definirea regulilor si exprimate pe scurt in tabelul FAM (tabelul 13.10). Valorile in tabelul FAM, bineinteles, sunt datele de iesire de control.

Etapa 4 Definirea conditiilor initiale si, simularea pentru patru cicluri. De cand sarcina mainii este de a controla coborarea descendenta in timpul apropierii si a aterizarii, vom incepe cu avionul la altitudinea de 1000 feat, cu o viteza de coborare de -20 ft/s. Vom folosi ecuatiile urmatoare pentru a marii variabilele vectori pentru fiecare ciclu:

v_i+1=v_i+f_i

h_i+1=h_i+v_i

tabelul 13.7

Valorile de apartenenta pentru inaltime

Inaltimea(ft)

Larg (L)
Mediu(M)
Mic (S)
NZ

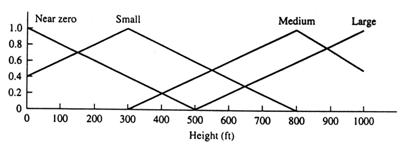
figura 13.31

tabelul 13.8

Valorile de apartenenta pentru velocitate

Velocitate verticala(ft/s)

Up large(UL)

Up small Us

Zero (Z)

DS

DL

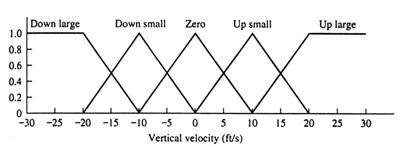
figura 13.32

tabelul 13.9

Valorile de apartenenta pentru forta de control

Forta output(lbs)

UL

US

Z

DS

DL

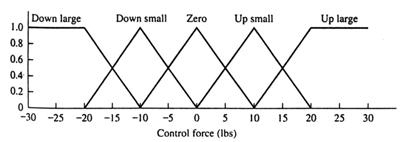
figura 13.33

tabelul 13.10

Tabelul FAM

Velocitatea

Inaltimea	DL	DS	Zero	US	UL
L	Z	DS	DL	DL	DL
M	US	Z	DS	DL	DL
S	UL	US	Z	DS	DL
NZ	UL	UL	Z	DS	DS

Inaltimea initiala, h₀:1000ft

Viteza initiala, v₀=-20 ft/s

F₀ de control: sa fie calculat

Inaltimea h aprinde "fires" La 1.0 si M la 0,6.

Viteza v aprinde doar ∆L la 1.0.

Inaltimea    Viteza Date de iesire

L(l.0)     si ∆L(l.0) => Z(l.0)

M(0,6) si eL(l.0) => US(0,6)

Noi defuzzificam folosind metoda centrului de greutate si avem f₀=5,8 lbs. Aceasta este forta de iesire calculata din conditiile initiale. Rezultatele ciclului 1 apar in fig. 13.34. Acum, calculam valorile noi a variabilelor vectori, si de iesire pentru urmatorul ciclu,

h₁=h₀+v₀=1000+(-20)=980 ft

v₁=v₀+f₀=-20+5,8=-14,2 ft/s

Inaltimea h₁=980 ft aprinde L la 0,96 si M la 0,64

Viteza v₁=-14,2 ft/s aprinde ∆S la 0,98 si ∆L la 0,42

Inaltime Velocity Date de iesire

L(0,96) si ∆S(0,58) => ∆S(0,58)

L(0,96) si ∆L(0,42) => Z(0,42)

M(0,64) si ∆S(0,58) => Z(0,58)

M(0,64) si ∆L(0,42) => US(0,42)

Gasim centrul de greutate a fi f₁=-0,5 lbs

Rezultatele sunt aratate in figura 13.35

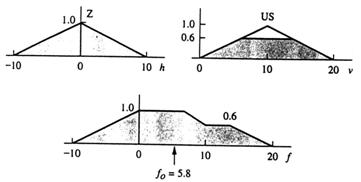
Figura 13.34

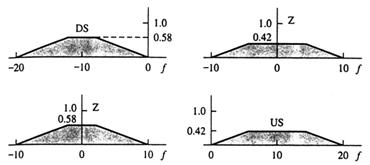
Figura 13.35

Caculam valorile noi a variabilelor vectori si datele de iesire pentru urmatorul ciclu.

h₂=h₁+v₁=980+(-14,2)=965,8 ft

v₂=v₁+f₁=-14,2+(-0,5)=-14,7 ft/s

h₂=965,8 ft aprinde L la 0,93 si M la 0,67

v₂=-14,7 ft/s aprinde ∆L la 0,93 si ∆S la 0,57

Inaltime Viteza Datele de iesire

L(0,93) si ∆L(0,43) => Z(0,43)

L(0,93) si ∆B(0,57) => ∆S(0,97)

M(0,67) si ∆h(0,43) => US(0,43)

M(0,67) si ∆S(0,57) => Z(0,57)

Gasim centrul de greutate pentru acest ciclu a fi f₂=-0,4 lbs. Rezultatele apar in fig. 13.36. Din nou, calculam valori noi pentru variabilele vectori si datele de iesire:

h₃=h₂+v₂=965,8+(-14,7)=951,1 ft

v₃=v₂+f₃=-14,7+(-0,4)=-15,1 ft/s si pentru inca un ciclu avem

h₂=951,1 ft aprinde L la 0,9 si M la 0,7

v₃=-15,1 ft/s aprinde ∆S la 0,49 si ∆L la 0,51.

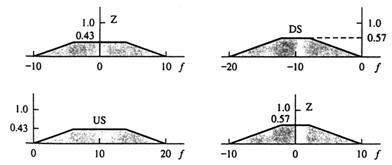
Figura 13.36

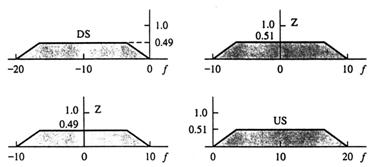
Figura 13.37

Inaltime        Velocity Date de iesire

L(0,9) si ∆S(0,49) => ∆S(0,49)

L(0,9) si ∆L(0,51) => Z(0,51)

M(0,7) si ∆S(0,49) => Z(0,49)

M(0,7) si ∆L(0,51) => US(0,51)

Rezultatele sunt aratate in fig. 13.37, cu o valoare centru de greutate defuzzificata de f₃=0,3 lbs. Acum, calculam valorile finale pentru variabilele vectori pentru a termina simularea,

h₄=h₃+v₃=951,1+(-15,1 )=936,0 ft

v₄=v₃+f₃=-15,1+0,3=-14,8 ft/s

Sumarul rezultatelor simularii celor patru cicluri este prezentat in tabelul 13.11. Daca povestim despre viteza de coborare si altitudine (inaltime), avem profilul descedent aratat in figura 13.38, care apare a fi un start rezonabil la curba parabolica dorita aratata la inceputul problemei.

Aplicatiile industriale

Doua articole recente au furnizat o excelenta recapitulare a bogatiei produselor industriale si "consumer appliances" ce aduc aplicatii logice vagi pietei. Un articol descrie aplicatiile logice vagi intr-o duzina de "household apliances" [Quail si Adnan, 1992] si alte afaceri cu o suita larga de componente electronice in general domeniul echipamentelor de procesat imaginea [Takagi, 1992] de fapt, o conferinta recenta a abordat total cu aplicatii industriale de control vag.[Yen et a1.,1992].

Tabelul 13.11

Sumar al rezultatelor simularii four-cycle

	Ciclul 0	Ciclul 1	Ciclul 2	Ciclul 3	Ciclul 4
Inaltimea, ft
Velocitatea,ft/s
Forta de control

Figura 13.38

Putini dintre noi a putut prevedea revolutia, dar teoria sirurilor vagi s-a produs deja. Dr. Zadeh insusi prezicea ca logica vaga va fi o parte a fiecarei "appliance" pretuite nu pe cal-putere ci pe IQ. [Rogers si Hoshai, 1990]. In Japonia, revolutia a fost asa de puternica ca "logica vaga" a devenit un obisnuit slogan publicitar [Reid, 1990]. Pe cat vreme lumea din est egaleaza lumea vaga cu forma a inteligentei artificiale,lumea din vest inca asociaza cuvantul "derisively" cu contextul "stiinta imprecisa sau aproximativa".

Consumatorul in general cumpara noi "appliances"bazate pe abiiitatea lor de a "streamline" munca de acasa si de a folosi timpul disponibil mult mai eficient. Logica vaga este incorporata de toata lumea in "appliances" pentru a indeplini aceste goluri, in principal in mecanismul de control modelat pentru a le face lor munca. "Appliances" cu controlori logici vagi realizeaza consumatorul cu decoruri optime ca mult mai apropiate perceptiile si reactiile umane decat aceste asociate cu un sistem de control standard. Produsele cu "fuzzy logic monitor user-defmed settings" care fixeaza automatic echipamentul pentru a functiona la nivelul preferat a utilizatorului pentru o sarcina data. De exemplu, logica vaga se potriveste de minune de a face ajustari in temperatura, viteza, si alte conditii de control gasite intr-o mare varietate a produselor consumate [Loe, 1991]. Putine exemple de aplicatii logice vagi de folosinta sunt realizate pentru a lamuri cititorul de potentialul imens a acestei tehnologii noi relative.

Controlul logic vag a presiunii sangelui in timpul anesteziei

In aceasta aplicatie [Meier et al.,1992] un controlor logic vag a fost folosit de a controla presiunea din arterele prīncipale (MAP), care au fost luate ca dimensiuni ale profunzimii anesteziei.Prīncipalul motiv pentru a automatiza controlul profunzimii anesteziei este de a elibera anesteziatul asa incat el sau ea poate indrepta atentia la alte sarcini la fel de bine - ca de exemplu controland, balasand, fluidul, ventilatia, si aplicatia medicamentului - ce nu poate fi inca automatizat adecvat si astfel pentru a creste siguranta pacientului. Pentru ca un proces biologic ,ca anestezia, sa aiba o structura timp-variabiI modeland evidentiaza utilizarea controlorilor cu reguli de baza ca controlorii vagi. Procesul modelului aici a fost iterativ, si punctele de referinta a functiilor de apartenenta ca si regulile lingvistice au fost determinate de incercare si eroare.

Regulile de control au fost folosite erorii dintre valoarea MAP dorita si cea actuala la fel de bine ca integrarea erorii.

Inelul de control are structura aratata in fig. 13.39. aici sunt doua lucruri diferite de tulburari: (1) tulburari "surgical", (2) masurarea galagiei si "artifacts".

Profunzimea anesteziei este controlata folosind o amestecare de medicamente ce sunt injectate in vene sau inhalate ce gaze. Cei mai mutti agenti descreste MAP. De-a lungul inhalarii gazelor, "isofluorane" este folosit in mare masura, cei mai adesea intr-un amestec de la 0 la 2 procente de volum de "isofluorane" in oxigen si/sau "nitrons oxide". Pentru simularea si controlul modelului relatia dintre concentratia abundenta a "īsotluorane", u(t), si presiunea sangetuī rezultanta, y(t), este modelata ca o suma a primilor temeni de pnm rang, fiecare are o pura intarziere (modelul in fig. 13.39 include pacientul si de asemenea circuitul semi inchis). Etapa raspuns, h(t), corespunzator datei de intrare unitate poate fi scrisa cum urmeaza, unde

k₁=-3, k₂=-7,3, t₁=-230, t₂=101s, α₁=0,01, α₂=0,006:

(13.36 a) h(t)=f₁(t)+f₂(t)

(13.36 b) K₁α₁ exp[-α₁(t-t₁)] pentru t>t₁

(13.36 c) f₂(t)=K₂α₂ exp[-α₂(t-t₂)] pentru t>t₂

Este presupus ca t₁=C₁T si t₂=C₂T. Transformarea Z a functiei de transfer a etapei raspuns a ecuatiei (13.36 a), poate fi exprimata ca in ecuatia(13.37), unde Y(z) si U(z) sunt z transformari al presiunii sangeiui cu date de iesire si respectiv concentratia "isofluorane" ca date de intrare:

unde b₁=k₁α₁

b₂=- k₁α₁ exp (-α₂T)

a₂=exp(-α₁T) exp(-α₂T)

unde ecuatia (13.37) este rescrisa in forma recursiva cu T=10s, a₁=-1,221, a₂=0,335, b₁=-0,030, b₂=0,048, b₃=-0,017 si b₄=0,041, avem

(13.38) y(kT)=-a₁y[(k-1)T]-a₂y[(k-2)T]+b₁u[(k-c₁)T]+b₂u[(k -c₁-1)T]+b₁u[(k-c₂)T]+b₄u[(k-c₂-1)T]

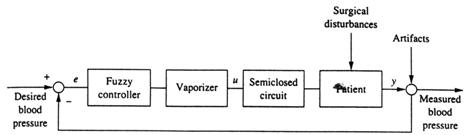
figura 13.39.

Pentru controlorul vag, eroarea e(t) si integrala erorii ∫e(t) sunt folosite pentru calcularea variabilei de control u(t) eroarea e(t) este definita ca

e(t)=d(t)-y(t)

unde d(t) este presiunea sangelui dorit.

Regulile lingvistice care descriu actiunile anesteziatului sunt date in tabelul 13.12 . Tabelul FAM pentru aceste reguli este dat in tabelul 13.13. Abreviatiile NB, NS, ZE, PS, PB, si PV se refera la variabilele lingvistice "negativ mare", "negativ nou", "zero", "pozitiv mic", "pozitiv mare", si respectiv "pozitiv foarte mare". In tabelul 13.13, simbolul slash este un exclusive-or. Functiile de apartenenta folositi in acest caz sunt functii "forma de clopot" ce pot fi descrise de urmatoarea ecuatie exponentiala, unde ζ este valoarea de intrare si λ, schimbatorul "shifting" functiei in relatie cu zero:

η=exp[-k(ξ-λ)²]

Factorul k determina latimea clopotelului (Gaussian). Punctele de referinta pentru functiile de apartenenta sunt in tabelul 13.14. Functiile de apartenenta sunt aratate in figura 13.40, unde o valoare k=5 este folosita pentru toate functiile de apartenenta pentru e si pentru u.

Rezultatele pentru simulare folosind regulile lingvistice si punctele de referinta realizate in tabelele 13.12-13.14 sunt aratate in figura 13.41. O compozitie max-min si un centru a "gravity defuzzification method" au fost folosite aici pentru a evalua regulile lingvistice.

Tabelul 13.12

Regulile lingvistice

Regula numarul:	Input         e	Input         ∫e	Output               u
	NS		PB
	PS		PS
	NB		PV
	PB		ZE
	ZE	ZE	PM
	ZE	PS	PS
	ZE	NS	PB
		NB	PV
		PB	ZE

Tabelul 13.13

FAM pentru cele noua reguli ale tabelului 13.12

E/∫e	NB	NS	ZE	PS	PB
NB	PV	PV	PV	PV	PV\ZE
NS	PB\PV	PB	PB	PB	PB\ZE
ZE	PV	PB	PM	PS	ZE
PS	PS\PV	PS	PS	PS	PS\ZE
PB	ZE\PV	ZE	ZE	ZE	ZE

Tabelul 13.14

Punctele de referinta a functiilor de apartenenta

	Input e, (mm Hg)	Input ∫e,(mm Hg ∙s)	Output	Output u, (%)
NB			ZE
NS			PS
ZE			PM
PS			PB
PB			PV

In figura 13.41 la 200 s sirul de valori este ridicat de la 80 mm kg la 88mm Hg. La 800 si la 1400s doua tulburari sunt aplicate . Controlorul este rapid, si doar "overshoot" mic este observat.

La 2100s sirul de valori este redus la 84 mm Hg.

Aplicatiile logice vagi la echipamentele de procesat imagini

Aceasta parte discuta despre trei feluri de echipamente de domeniul preprocesarii imaginii [Takagi,1992]. Primul este un mecanism automat de focalizare pentru o camera de 35mm. AI doilea este un controlor de stabilizarea imaginii pentru camera video. Al treilea este o televiziune.

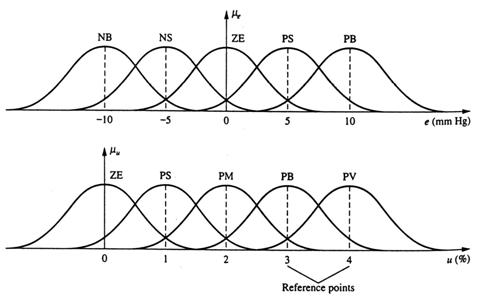
Figura 13.40

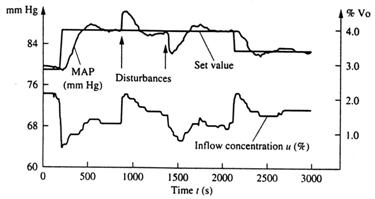
Figura 13.41

Sistemul automat de focalizare pentru o camera de 35 mm. O mare camera Asion a aplicat logica vaga pentru a decide aupra carui obiect in campul de vizualizat ar trebui focalizat si apoi pentru a controla mecanismul automat de focalizare de a focaliza asupra acel obiect. [Shingu si Nishimori, 1989].

Prima data distantele dintre trei puncte din campul vizualizat (figura 13.42) sunt masurate. Folosind aceste date si relatiile intre ele, logica vaga decide unde punctul focus dorit se aseaza si apoi se focalizeaza in acel punct . Tabelul 13.15 arata regulile folosite in simularile experimentale. Produsul final poate avea mai multe reguli. In tabelul 13.15 simbolurile L (stanga), C (centru), si R (dreapta) descriu trei puncte masurate aratate in figura 13.42. De asemeni, simbolurile Pl, Pc, si Pr denota plauzibilitatea gasirii obiectului focusului la punctele L,C, sau respectiv R.

Comparand tigura 13.43 a si 13.43 b, vedem ca figura 13.43 a principalul obiect la stanga, atat cat timp in figura 13.43 b are subiectul principal in centru. Oricum, relatia este L<C<R in cele doua cazuri si amandoua satisfac reguiile doi si cinci, listate in tabelul 13.15. In acest caz decizia depinde de vaiorile lui L,C si R; si aceasta comparatie e facuta cu ajutorul functiilor de apartenenta . Este mult mai dificil pentru regulile logice binare de a modela aceasta situatie pentru ca o gramada de reguli sunt cerute.Cateva reguli vagi, oricum, pot usor avea de a face cu aceasta problema.

Stabilizarea imaginii pentru camere de luat vederi

Un proeminent produs electronic Asion a aplicat logica vaga pentru a determina daca mi- scarea imaginii in oglinda imaginii camerei video este cauzat de tremurarea mainii tinand camerele video sau de miscarea inerenta a obiectului, flind fotografiat [Egusa et al.,1992]. Aceasta camera a fost pusa pe piata in 1990.

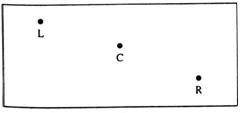
Figura 13.42

Tabelul 13.15

Fuzzy rutes for camera autofocus system

Daca C este aproape, atunci Pc este mare

Daca L este aproape, atunci Pl este mare

Daca R este aproape, atunci Pr este mare

Daca L este departe si C este medie si R este aproape, atunci Pc este foarte mare

Daca R este departe si C este medie si L este aproape, atunci Pc este foarte mare

Ca consumator de camere de tuat vederi devine mai usor si mai portabil, problema cu tremurarea s-a inrautatit si are nevoie de rezolutie. Pentru a aborda aceasta, o bucatita LSI obisnuita (imaginea senzorului laser) detecteaza vectorul miscare si un sistem vag decide daea miscarea este cauzata de tremurare. Procesarea semnalului digital folosit pentru a compensa daca aceasta este intr-adevar cazul.

Datele de intrare catre sistemul vag sunt patru vectori mīscare, fiecare venind din cele patru regiunī in care imaginea a fost divizata, si ratele lor de schimbare. Fiecare din aceste patru regiuni este mai departe impartita in alte 30 de domenii mai mici. Doua cadre succesive sunt comparate (vezi fig.13.44) pentru a calcula valorile diferentiale spatiale pentru fiecare domeniu. Aceste diferente sunt peste 30 de domenii intr-o regiune pentru a produce o diferenta neta Ri pentru i. Pentru fiecare regiune, cativa vectori "one-shift" rezulta in valorile mici ale Ri. Aceasta schimbare minimala este vectorul miscare v, pentru aceasta regiune. Rationamentul vag foloseste valorile v, ca date de intrare pentru a detecta tremurarea mainii. Cand aceasta este cazul si acolo nu e nici un obiect miscator atunci minimul Ri este aproape zero. Daca acolo este un obiect mic miscator in imagine si mana este ferma, atunci domeniul corespunzator obiectului miscator are o valoare diferentiala spatiata care este diferita de domeniile inconjuratoare. Oricum, valorile Ri nete ar trebui sa fie mici.

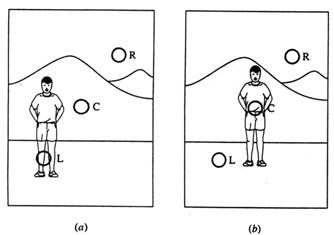
Figura 13.43

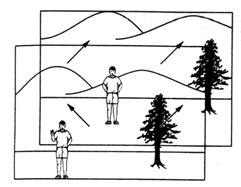
Figura 13.44

Cand acolo sunt amandoua, miscarea mainii si miscarea obiectului, atunci minimul Ri contribuie sa fie mai mare decat in cazul in care nu exista nici un obiect miscator. The time "derivatives" ale valorile Ri sunt, deasemeni, folosite de sistemul vag. Aceasta incorporeaza informatia despre marimea si miscarea obiectului miscator. O regula folosind acestea poate fi: Daca cei patru vectori mīscare sunt aproape paraleli, si "their time differential" este mica, atunci tremurarea mainii este intamplatoare si directia tremurarii este directia vectorilor miscare.

Odata ce directia miscarii e cunoscuta, cadrul din tampon este deplasat in directia opusa a acestei miscari, in asa fel stabilizarea este obtinuta. Aceasta procesare a imaginii devine doar posibila pentru ca toate semnalele folosite sunt "digitized".

Television sets

O fabrica bine cunoscuta din Aia de produse elctrice consumatoare a folosit concluzia vaga pentru controiarea calitatii imaginii receptiei TV ce a aparut pe piata in toamna 1990 [Hayashi si Yoshida, 1991]. Sistemul vag controleaza contrastul, luminozitatea,viteza modulatiei si precizia. Parametrii de intrare sunt luminozitatea ambientului din camera si distanta telespectatorului de multime. Un principiu de baza obisnuia sa construiasca reguli vagi ce pot fi exprimate astfel: "Cand camera este luminata si telespectatorul este foarte departe atunci regiunea limitata pe poza ar trebui sa fie precisa si clara", pe cand "Daca telespectatorul este aproape si intr-o camera intunecoasa atunci precizia ar trebui sa fi mai putin buna deoarece componentele de inalta frecventa sunt acompaniate de zgomot." Tabelul 13.16 realizeaza alte cateva principii folosite.

Regulile actuale din sistem sunt mult mai detaliate pentru control mai fin. Exista patru tunctii de apartenenta pentru luminozitate, trei pentru distanta, si sapte pentru variabilele de iesire.

Tabelul 13.16

Reguli de inferenta vagi  pentru controlul calitatii imaginii a TV set

Room light

Distance from TV to viewer

	bright	dark	far	Mid	near
Contrast	big	small	big	Mid	small
Brightness	big	small		Same
Velocity modulation	big	small	big	Mid	small
Sharpness	big	small		Same

Concluzia este legata de metoda max-min-gravitate si este implementata de un tabel "lookup" in produsul final.

Luminozitatea camerei este calculata cu un senzor de lumina pentru a ne da o valoare din cele opt valori. Distanta tetespectatorului este calculata localizand comanda de la distanta si are trei posibile valori. Microcontrotorul foloseste acestea pentru a consulta tabelul "lookup" si patru valori de iesire sunt primite. Acest proces este repetat la fiecare 50 milisecunde.

Controlul vag adaptabil obisnuit a sistemului de incalzire de la casa

O companie europeana a introdus logica vaga la noua generatie de controlori de cuptor intr-un sistem de incalzire intr-o casa privata [AltrocK et. a1.,1993]. In sistem, atat controlorul logic vag cat si sistemul de control convetional erau implementate pe un microcontrolor de 8 bits standard. Controlul logic vag garanteaza adaptarea optima la schimbarile obisnuite de caldura folosind un senzor mai putin decat sistemul din generatia anterioara.

Un tip de sistem de incalzire centralizata traditional arde un combustibil tip diesel in cuptorul lui pentru a incalzi apa de rezerva (fierbator). Din fierbator, apa incalzita este distribuita de un sistem teava spre radiatoarele individuale din casa.

Pentru a satisface diferitele nevoi ale clientului in cuptor trebuie sa fie constant ajustata temperatura fierbatorului in relatie cu temperatura exterioara (caldura caracteristica). Pentru a masura temperatura exterioara, un senzor este instalat la exteriorul casei. Figura 13.45 infatiseaza schema de baza a unui asemeni sistem.

Structura de baza a unui controlor pentru acest sistem este aratata in figura 13.46. Controlorul insusi realizeaza o caracteristica inchis-deschis.

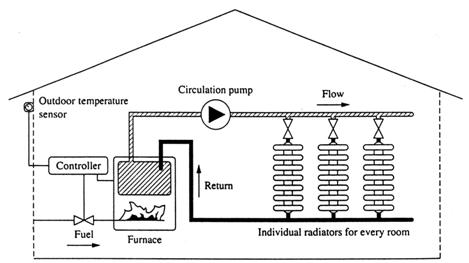
Figura 13.45

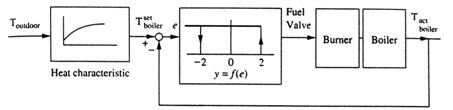
Figura 13.46

Daca temperatura apei din cuptor scade la 2°C sub temperatura fixata, valvele combustibulului se deschid si sistemul de ardere incepe psocesui de ardere. Cand temperatura apei din fierbator creste la 2°C deasupra temperaturii fixate, valvele combustibulului se inchid. Traditional, temperatura fixata a fierbatorului este o functie cu parametrii T^set_boiler=f(T_outdoor) definita de standardele europene in 1950. Functia depinde foarte mult de temperatura de afara care era apropiata atunci cand cele mai multe case aveau doar un singur izolator termal amarat. Acest model este acum invechit datorita imbunatatirii izolarii casei. Alti factori ca de exempIu ventilatia, usa/geam deschisa si stilul de viata persoanei trebuiesc a fi considerate la fel de mult.

Cel mai important criteriu descriind exemplele de cerere de caldura obisnuita individuala provine din curba de consum a energiei actuale a casei, care este masurat de raportul deschis-inchis a arzatorului. Un exemplu de asemenea curba este data in figura 13.47. De la curba, 4 parametrii descriptivi sunt derivate: 1. Consumul de energie electrica curenta, indicand incarcatura curenta.

2.Tendinta perioada-medie I, indicand faze de incalzire inalta si joasa incalzire

Tendinta perioada-mica II,indicand perturbatii ca deschizaturi usa-fereastra

Consumul de energie medie de ieri indicand nivelul de incalzire

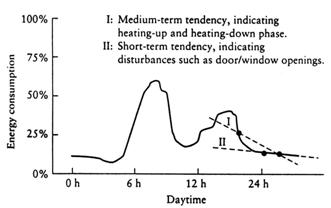
figura 13.47

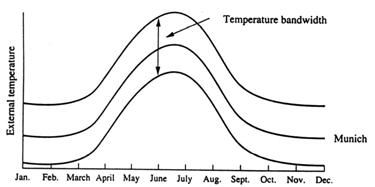
figura 13.48

Acesti 4 parametri descriptivi au fost folositi pentru a forma reguli heuritice pentru determinarea temperaturii boilerului apropiate. Pentru a tine seama de formularea regulilor plauzibile (cum ar fi "temperaturile sub 0°C sunt rare in August'') temperatura rezultanta medie apropiata pentru acest sezon este si un parametru de intrare in sistem . Aceste curbe sunt date in figura 13.48. De cand curbele temperaturii medie sunt date, nici o temperatura rezultanta nu are nevoie de a fi masurata.Din acest motiv senzorul temperaturii rezultante poate fi eliminata.

Structura regulatorului furnarului nou este aratata in figura 13.49. Regulatorul vag foloseste un total de 5 date de intrare, 4 sunt derivate din curba consumului de energie folosind tehnici de filtrare, digitale convetionale, al cincilea este temperatura rezultanta medie. Acest input vine din tabelul de cautat din sistemul ceas.Productia sistemului vag reprezinta caldura estimata ceruta a casei, si corespunde valorii T_outdoor in controlorul convetional. (fig.13.46)

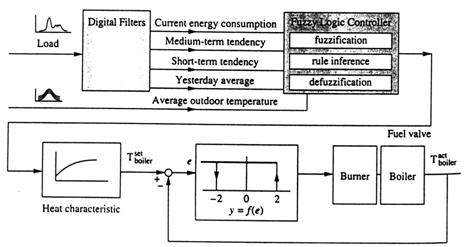
Fig. (13.49)

Obiectivul regulatorului vag este de a estima cerinta de caldura actuala a casei. Pentru aceasta, regulile daca-atunci au fost definite pentru a exprima heuristicile ingineresti. Ale estimarii parametrice:

Daca consumul de energie curenta este joasa

Si tendinta perioada-medie creste

Si tendinta perioada-mica descreste

Si media de ieri este medie

Si temperatura de afara medie este foarte joasa.

Atunci cerinta de caldura estimata este medie-ridicata

In tota1, 405 de reguli au fost definite pentru estimarea parametrica. Strategia dedusa a fost extinsa pentru a admite pentru a fi asociate cu un "rang al suportului", un numar intre 0 si 1 ce exprima importanta individuala a tiacarei reguli cu respectul fata de celelalte reguli. Aceasta permite pentru exprimarea regulilor, ca de exemplu:

Daca tendita perioada-medie este stabila

Si media de ieri este foarte inalta

Atunci caldura estimata este intre cea inalta, mai degraba multime ridicata.

Metoda dedusa pentru a reprezenta gradele individuale a raportului este bazata pe un rationament aproximativ si pe tehniciile Hartii asociativa vaga (FAM): dupa fuzzificare, toate regulile premise sunt calculate folosind aparatul minim pentru reprezentarea a AND-ului lingvistic operatorul maxim pentru reprezentarea a OR-ului lingvistic. Dupa aceasta gradul validitatii premisei este impovarat cu gradul individual suportului a regulei, rezultand in gradul adevarului pentru concluzie. In a 3-a etapa, toate concluziile sunt combinate folosind operatorul maxim. Rezultatul etapelor rezultate este un set vag. Centrul metodei defuzificarii maxime este folosita pentru a se indrepta catre valoarea reala din productia vaga.

Dupa completarea modelului regulatorului vag si definitia variabilelor lingvistice, functia de apartenenta, si regulile, sistemul a fost compilat catre hardware tinta, i.e., catre 8051 limbaje de asamblare. Cu aceasta tehnologie, controlul vag foloseste numai 2.1 bytes a domeniului ROM intern. Prin intermediul reprezentarii regulilor in matrice si tehnologiei dezvoltarii online, optimizarea sistemului logic vag complex continand 405 reguli au fost facute eficient. Relizarea sistemului a fost evoluat prin conectarea regulatorului conventional si a controlorului vag catre casa de stat. Un astfel de exemplu este aratat in fig. 13.50.

Rezultatul testelor realizarii comparative aratau ca controlorul vag a fost foarte sensibil la cerinta de caldura a casei. A fost foarte sensibil la schimbarile bruste a caldurilor cerute, ca reintoarcerea inlocuitorilor casei din vacanta. Suplimentar, eliminarea senzorului de temperatura exterioara costa cam 30$ in costurile de productie si chiar mai mult in costurile de instalare. Fixand regulatorul de temperatura a boilerului "beneath" nivelul tipic folosit de un regulator vag in perioade de domenii joase, regulatorul vag a salvat de fapt energia. (Altrock et.al., 1993).

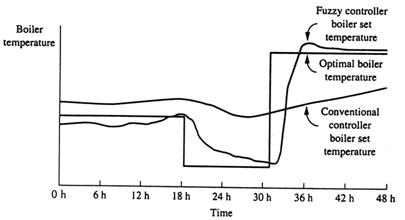
Figura 13.50

Sisteme vagi adaptabile

Un sistem vag conventional (fig. 13.51) de obicei ia forma unui model de ajustare iterativ. Intr-un astfel de sistem valorile de intrare sunt normalizate si convertite la reprezentatiile vagi, regula de baza a modelului este executat (intr-un mod paralel) pentru a produce o regiune vaga consecventa pentru fiecare variabila solutie, si regiunile consecvente sunt defuzzificate (convertite la valori fragile) pentru a gasi valoarea estimata pentru fiecare variabila solutie. Variabila solutie este controlul. O schimbare este facuta catre planta, a carei senzori culege, selecteaza, si reactioneaza in regulatorul vag la urmatoarea multime de vatori de intrare.

Regulile executate de un sistem de control vag conventional sunt deseori sisteme "time-series" sau procese stari-de baza. De exemplu, in controlul actiunii a turbinei de vapori, regulile tipice (Cox, 1993) sunt :

Daca temperatura (t-1) este foarte mare si temperatura (t) este mare, atunci viteza (t) este putin deschisa.

Daca [temperatura (t)-temperatura (t-1)] este putin scazuta, atunci viteza (t) este putin inchisa. Figura 13.51

Daca viteza (t-1) este deasupra vitezei (t), atunci presiunea de injectie este larg crescuta.

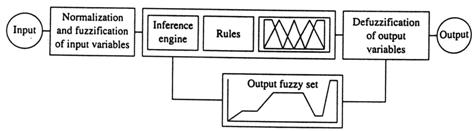
Figura 13.51

Sistemul conventional ia senzori de citire a temperaturii turbinei si presiunea in cadrul de timp curent (t) si le compara cu valori senzori, luate Ia timpul (t-1). Apoi face schimbari in suprafate de control curenta (ajusteaza viteza) pe baza diferentelor. Dar proceseaza datele lui de intrare impotriva unui set fixat de intructiuni; nu este adaptabil.

Pe de alta parte, un sistem de control adaptabil ajusteaza suprafata de control in concordanta cu parametrii semnal, variante. Pentru a vedea cum un sistem adaptabil lucreaza, noi ne putem vedea cum sa facem un "simple nonadaptive automobile speed control system" (vezi fig. 13.52, stanga) "adaptive". In acest sistem, decorul de viteza ceruta initial cauzeaza regulatorul pentru a deschide sau pentru a inchide motorul la o rata sigura (Cox, 1993). O schimbare intr-un moment de incarcat cauzata de o schimbare in gradul de drum este citita ca o peturbare de sistem si poate modifica specificatia. Actiunea cauzeaza o crestere sau o descrestere in viteza motorului care este citita de "tachometer". Daca viteza depaseste decorul, atunci cerinta de viteza curenta este redusa. Aceasta viteza redusa este pasata catre controlor, si se repeta ciclul.

Sistemul deja descris poate fi facut adaptabil adaugand o facilitate pentru schimbarea marimii pasului a controlorului pe o lungime metrica (fig. 13.52, dreapta). Rezolva aceasta problema prin modificare greutatii a pasului semnal de viteza de o regula adaptabila. Aceasta regula intensifica sau diminueaza semnalul de viteza depinzand daca a fost schimbata de cand a fost ultima data citita. O regula tipica poate fi de a dubla marimea pasului daca nu a fost nici o schimbare, si de a o imbunatati altfel.

Desi este o imbunatatire peste un sistem neadaptabil, sistemul aratat in fig. 13.52, inca lipseste o cale de mijloc prin care regulatorul se poate reorganiza permanent asa ca e mai bine de avea a face cu noi clase de stimuli. O combinatie a sistemului de control adaptabil cu logica vaga poate realiza acest sistem organizare-individuala.

Un sistem logic vag adaptabil, nu ajusteaza numai conditiile timp- sau "process-phased' ci si schimba sistemul de control suport. Aceasta este, un sistem adaptabil modifica caracteristicile regulilor, topologia multimilor vagi, si metoda de defuzzificare bazate pe metriciile apropiate estimate (sau, mai simplu, cat de repede se apropie sau se indeparteaza o stare "goal".

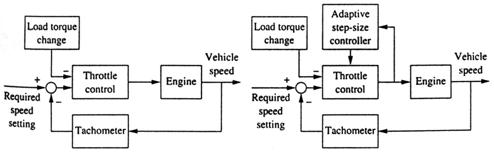
Fig. 13.52

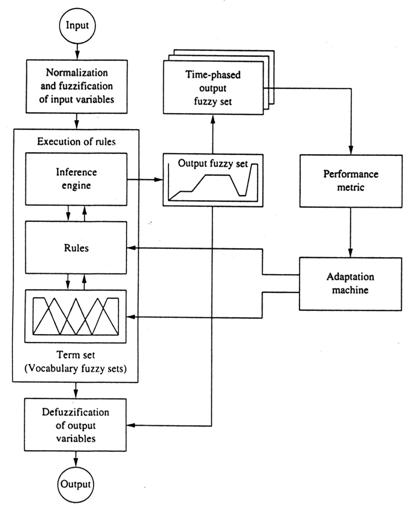
Fig. 13.53.

Ca in figura 13.53 aratata, un sistem vag adaptabil duce la o concluzie vaga conventionala, incercand sa dezvolte o valoare pentru variabila solutie din regulile in "its knowledge repository". Trasaturile regiunii vagi creata pentru variabila solutie sunt adunate intr-un buffer timp- sau proces "phased" unde ele pot fi accesate. Pentru a produce un semnal feedback catre modelul vag, o metrica performanta, deseori un sistem expert sau doar un algoritm ce masoara schimbul dintre senzori de masurare, Interogheaza desfasurarea si sirul adunat de solutii trecute (la fel de bine, poate, ca un sir de statistici asociata cu modelul "ongoing"). Acest semnal este feedback intr-o masina adaptabila ce decide ce schimbari se fac in modelul vag principal.

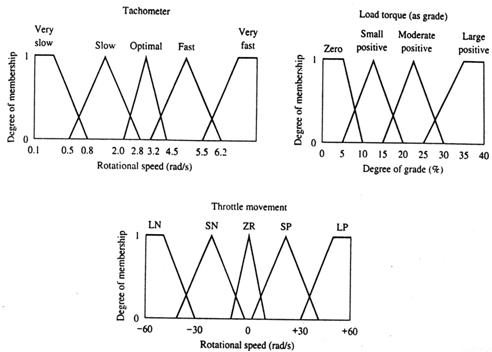
Figura 13.54

Intr-un regulator vag adaptabil simplu - de exemplu, regulatorul vitezei vehicului mentionat mai sus - sunt doua date de intrare si o singura data de iesire. Procesul citeste viteza vehicului curenta si incarcatura momentana produsa de gradul drumului (doua date de intrare) si ajusteaza "beregata" pentru a creste sau a descreste viteza masinii (data de iesire). (fig. 13.54).

Momentul controlului este variabila solutie (data de iesire) din regulatorul vag. Raspunsul este dezvoltat prin aplicarea tuturor reguliior si apoi prin luarea valorilor estimate a regiunii vagi rezultata. Exemple a catorva reguli pentru regulatorul de viteza sunt:

Daca "tachometer" este foarte incet si incarcatura momentului este zero, atunci "beregata" este larg pozitiv.

Daca "tachometer" este incet si incarcatura momentului este putin pozitiva, atunci "beregata''' este putin pozitiva.

Tabelul FAM pentru aceste reguli este o matrice 4x5 aratat in tabelul 13.17.

Tabelul 13.17.

Tabelul FAM a sistemului de control a vitezei masinii

Tachometer

Load torque	Very slow	Slow	Optimum	Fast	Very fast
Zero	LP	SP	ZR	SN	LN
Small positive	LP	SP	ZR	ZR	SN
Moderate positive	LP	SP	SP	SP	ZR
Large positive	LP	LP	LP	LP	SP

Incercand de a mentine un raspuns a suprafetei de control consistent, un regulator vag autoadaptabil reorganizeaza suprafata de control insusi pentru a intalni obiectivele echilibrului plantei si stabilitatea sistemului. Regulatorul indeplineste adaptarea prin masurarea distantei din regiunea de echilibru in suprafata de control catre regiuni de tensiuni de suprafata crescanda­ aceasta este, catre domenii de pe suprafata ce apar a fl noi domenii de echilibru. Sunt cateva interconectate intelese prin a permite un sistem vag pentru a adapta. Acestea include conducerea importantelor, influentelor, atasate regulilor, dinamica evitand de regiuni vagi, modificare structurala a multimilor vagi, si selectia a metodelor alternative a defuzzicarii. Primele doua sunt cele mai importante.

Regulile importante de influenta, intr-un sistem adaptabil trebuie sa fie adaugate lui FAM ca alta dimensiune. Ei tin contributia de influenta conectata cu fiecare regula si sunt factori de care adevarurile prime diferite sunt multiple ca un sistem care se adapta la mediul lui, ele se pot situa de la 0 catre, dar nu incluzand, 2. Cand importanta, influenta, "greutatea", este mai mica decat 1, atunci adevarul premisei este redus, cand influenta, importanta, "greutatea", este mai mare decat 1, atunci adevarul premisei este crescuta. Aceste influente, "greutati", determina cat de mult regula afecteaza rezultatul final a modelului.

In general, algoritmul de modificare a influentelor, "greutatilor", este destul de simplu: El se compune din multiplicarea "greutatilor" diferite de catre un factor eroare. ln atrenamentul supervizat, factorul eroare este ratia datei de iesire a sistemului actual catre data de iesire corecta. Intr-un mod autoadaptabil, este distanta patratica principala de la centrul regiunii de control optime catre centrul raspunsului sistemului.

Tabelul 13.18

Contributia matricii de greutate pentru un model vag adaptabil (Cox, 1993)

Tachometer

Loard torque	Very slow	Slow	Optimum	Fast	Very fast
Zero
Small positive
Moderate positive
Large positive

Cand un model vag adaptabil este initializat, toate "greutatile" sunt fixate pentru a se uni asa ca nici o modificare a adevarului prim nu este indeplinita. Dupa ce sistemul adaptabil a fost lansat pentru un timp, "greutatile", vor expune o tendinta fata de domeniile unde cea mai mare cantitate de date sunt localizate. Tabelul 13.18 arate o matrice de "greutate" de contributie dupa cateva epoci de lansare. Notam tendinta generala fata de cea mai joasa regiune dreapta a FAM-ului indicand ca cele mai multe date sunt "cazute" catre acest domeniu. Amplificare a regulilor de "greutate" inseamna ca sistemul se adapta la o schimbare in regiunea lui centrala de control.

Schimband regiunile este o alta metoda pentru sistemele adaptabile vagi. Sistemele vagi adaptabile trebuie sa organizeze sirurile lor de termeni in raspuns pentru a schimba in mediul lor de operare. Sirurile de termeni sau vagi sunt limitate in concordanta cu feedback-ul din ciclul de iesire a modelului anterior. Daca raspunsul sistemului din executia modelului precedent a fost deasupra valorii estimate sau dorita, atunci pentru fiecare sir vag in sirul de termeni ce a fost accesat in timpul executiei, domeniul este slab limitat. Aceasta este marginea stanga a domeniului ce este mutat slab catre dreapta si marginea dreapta este mutata slab catre stanga. Similar, daca raspunsul sistemului a fost inferior estimarii, domeniile implicate sunt slab catre epociile din stanga si din dreapta sunt mutate slab catre dreapta. (vezi fig. 13.55).

Modificarea regiunii vagi este fortata de o restrictie a sumei de acoperire permisa de-a lungul multimilor vagi. In concordanta cu aceasta restrictie, pentru o linie verticala desenata printr-o regiune de acoperire, adevarul de apartenenta a punctelor unde linia se intersecteaza cu multimile vagi trebuie intotdeauna sa totalizeze mai putin sau sa fie egala cu 1. Desi, evident, folositor in sistemele de control, sistemele vagi adaptabile sunt in particular apropiate in econometrie, marketing, proiect de management, transport si analiza "field terrain" (Cox.,1993). Viitorul apropiat va arata o siguranta graduala a tehnologiilor organizate-sigure ca logica vaga, retele "neural", si algoritme genetice. Sistemele vagi adaptabile par o fundatie potrivita pentru integrarea usoara si pentru "deployment" ergonomic a acestor tehnici. In afaceri folosesc logica vaga mai mult in adresarea problemelor adanci complicate si de calcul, nu doar logica vaga va castiga o acceptare mai larga de catre designerii de proces ci si vor adapta sistemele vagi.

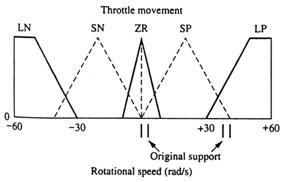
Fig. 13.55

Sumar

Noua generatie de regulatori logici vagi este bazata pe integrarea de regulatori conventionali si vagi. Tehniciile adunate vagi au fost de asemeni folosite pentru a extrage regulile Daca-Atunci lingvistice din datele numerice. In general, tendinta este catre compilatia si "fashion" de diferite forme de reprezentatii de cunostinte pentru cea mai buna identificare posibila si control a sistemelor complexe rau definite. Cele doua noi paradigme- retele "neural" artificiale si sistemele vagi- incearca sa inteleaga un sistem "real-world" incepand din cele mai fundamentale surse de cunostinte, i.e., pacient si observatii luate cu grija, masuri, experienta si rationament intuitiv si hotarari, mai degraba decat incepand dintr-o teorie "preconceived" sau model matematic. Controlorii vagi avansati folosesc capabilitati de adaptare de a adapta "the vertices" suporturilor functiilor de apartenenta sau de a adauga sau de a sterge reguli de a optimiza indeplinirea si compensarea pentru efectele oricarei peturbatii interne sau externe. Invatand sistemele vagi incearca sa inveti functiile de apartenenta sau regulile. In plus, principiile algoritmilor genetice, de exemplu, au fost folosite de a gasi cel mai bun sir reprezentand o clasa optima de functii de apartenenta triunghiulare simetrice de intrare sau de iesire.