Figura R 3.4.1

Rezolvare: a) Fiind un sistem de forte coplanare (situat în planul Oxy), fortele vor avea proiectii doar pe axele Ox si Oy iar momentele acestor forte în raport cu punctul O vor fi perpendiculare pe planul Oxy, deci . Modulele momentelor vor fi calculate cu relatia (3.2) iar sensul cu regula burghiului drept.

Forta : , ,

( O apartine suportului fortei ).

Forta : , ,

( O apartine suportului fortei ).

Forta : ,

(având sensul axei Oz, proiectia este pozitiva).

Forta : ,

(deoarece are sensul opus celui pozitiv pe Oz, aceasta proiectie este negativa).

Momentul : .

Rezultatele au fost sintetizate în tabelul T 3.4.

Tabelul T 3.4

Se obtine torsorul

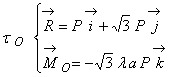
b) Ecuatia (3.14) a axei centrale ar 212y2420c e în cazul nostru forma :

.

c) Reprezentarea în functie de valorile parametrului real a torsorului de reducere si a axei centrale este data în figura R 3.4.2.

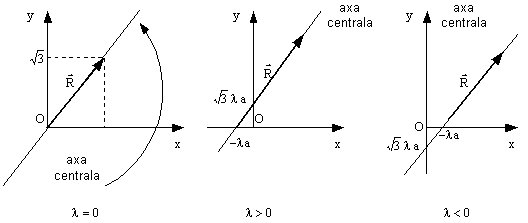
Figura R 3.4.2

R 3.5) Se dau fortele paralele , având directiile si sensurile din figura R 3.5 , modulele si punctele de aplicatie ,, respectiv. Se cere :

a ) Sa se determine torsorul de reducere în punctul O ;

b ) Sa se determine centrul fortelor paralele ;

c ) Sa se determine ecuatia vectoriala a axei centrale.

Rezolvare: a) Fortele se proiecteaza în adevarata marime pe Oz si dau momente doar pe axele Ox si Oy. Proiectiile acestor vectori sunt date în tabelul T 3.5.

Tabelul T 3.5

: ,

b ) Coordonatele centrului fortelor paralele sunt:

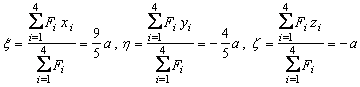
Rezulta .

c ) Ecuatia vectoriala a axei centrale este :

unde este o constanta arbitrara. Axa centrala este o dreapta paralela cu Oz si care contine punctul C .

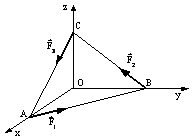
Figura R 3.5 Figura TC 3.1

3.10. Probleme propuse

3.10.1. Teste clasice

TC 3.1) Asupra piramidei triunghiulare OABC din figura TC 3.1, având laturile AB = AC = a si , actioneaza fortele si orientate ca în figura si având modulele . Se cere:

a)      Sa se reduca sistemul de forte în raport cu punctul O si sa se reprezinte grafic elementele torsorului de reducere obtinut;

b)      Cu ce este echivalent sistemul celor trei forte?

TC 3.2) Se considera paralelipipedul dreptunghic OABCO'A'B'C'de laturi OA = 3a , OC = 4a, OO'=12a solicitat ca în figura TC 3.2 , unde si M= 6aP. Pe latura O'A' actioneaza o sarcina liniar distribuita ( paralela cu Oz ) , ce variaza de la valoarea 0 în punctul O' la valoarea în punctul A'. Se cere :

a ) Torsorul de reducere în O ;

b ) Cu ce este echivalent sistemul dat ?

c ) Ce forta si ce moment trebuie sa se introduca în O pentru ca noul sistem de forte sa se reduca la o rezultanta unica iar axa centrala sa treaca prin A si B ?

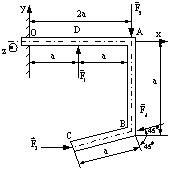
Figura TC 3.2    Figura TC 3.3

TC 3.3) O bara încastrata, având dimensiunile din figura TC 3.3, este solicitata de sistemul de forte coplanare , având directiile si sensurile din figura si modulele ,. Se cere :

a ) Torsorul de reducere în punctul O ;

b ) Cu ce este echivalent sistemul de forte ?

c ) Ecuatia axei centrale .

TC 3.4) Se dau fortele paralele , care actioneaza în punctele respectiv. Se cere:

a)      Sa se calculeze si sa se reprezinte torsorul de reducere în punctul O;

b)      Sa se determine centrul fortelor paralele si sa se determine axa centrala.

3.10.2. Teste grila

TG 3.1) Un sistem de forte oarecare se reduce la o forta unica, egala cu rezultanta , si care actioneaza pe axa centrala a sistemului daca elementele torsorului de reducere în raport cu punctul arbitrar O verifica conditiile:

a)      ; b) ; c) ;

d) .

TG 3.2) Punctul de aplicatie al fortei (N) are vectorul de pozitie (m) în raport cu originea sistemului cartezian Oxyz. Care este momentul fortei în raport cu diagonala AD a paralelipipedului dreptunghic din figura TG 3.2.

  a) ; b) 0 ; c) ; d) .

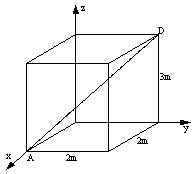
Figura TG 3.2 Figura TG 3.3

TG 3.3) Suma momentelor cuplurilor de forte ce actioneaza în lungul diagonalelor paralelipipedului dreptunghic din figura TG 3.3 este:

a)      ; b) ;

c) ; d) .

3.11. Indicatii si raspunsuri

TC 3.1) a)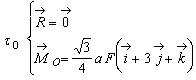

b) Sistemul de forte este echivalent cu un cuplu de forte de moment

TC 3.2) a ) Sarcina liniar distribuita este echivalenta cu forta rezultanta , aplicata în centrul D (2 a , 0 , 12 a ) al fortelor paralele distribuite .

: ,

b ) Sistemul de forte este echivalent cu un cuplu de forte de moment.

c ) Fie si forta si momentul necesar a fi introduse în punctul O . Noul torsor de reducere în O este :

: ,

Deoarece rezultanta este paralela cu axa centrala ( dreapta AB ) se impun conditiile. Ecuatiile axei centrale sunt :

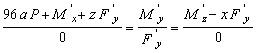
sau

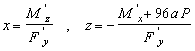
În plus , . Ecuatiile axei centrale sunt : x = 3 a , z = 0. Rezulta:

Sistemul se reduce la o forta unica daca , adica ( daca , notiunea de axa centrala îsi pierde sensul ) . Deci

unde este o constanta arbitrara .

TC 3.3) a )

: ,

b )

Sistemul de forte este echivalent cu o forta unica, egala cu rezultanta, situata pe axa centrala.

c ) .

TC 3.4) a) Vezi problema R 3.5.

;

b) Centrul fortelor paralele este punctul .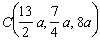

TG 3.1) Vezi "Cazuri de reducere a unui sistem de forte oarecare". Raspuns corect: b).

TG 3.2) Se foloseste faptul ca , unde si A(2, 0, 0), D(0, 2, 3). Raspuns corect: c).

TG 3.3) , unde este un vector liber, perpendicular pe planul ABC'O', de sens trigonometric si modul iar este un vector liber, perpendicular pe planul BCO'A', de sens trigonometric si modul . Raspuns corect: a).