Acest proiect isi propune sa gaseasca corelatia dintre nivelul produsului intern brut (PIB) in functie de nivelul veniturilor personale si al preturilor. Se va urmari influenta veniturilor, precum si a preturilor asupra produsului intern brut. Modelul econometric se va construi pe baza datelor obtinute de pe site-ul guvernului SUA (site-ul de unde au fost preluate datele este: https://www.bea.gov/bea/dn/nipaweb/NIPATableIndex.asp). Aceste date sunt structurate pe ani, incepand cu anul 1929 pana in 2006.

Se va studia influenta celor 2 factori separat: influenta veniturilor asupra nivelului produsului intern brut, apoi influenta indicelui preturilor asupra aceluiasi produs intern brut, urmand ca mai apoi sa se testeze modelele astfel obtinute, testari prelucrate cu ajutorul programului STATA9.

PIB = 174.051 + 1.185684 * venit + 3782509.88

Asadar, atunci cand venitul creste cu 1 miliard dolari, PIB-ul la nivelul SUA creste cu 1.18 miliarde dolari. Insa, pentruca nivelul produsului intern brut sa fie mai mare de 0 este nevoie de un nivel al veniturilor de peste 146.79 miliarde dolari (174.051/1.185684).

O prima analiza a parametrilor estimati ne arata ca acestia sunt viabili. Este testata egalitatea parametrilor cu 0, iar avand in vedere ca intervalul de incredere nu cuprinde valoarea 0 inseamna ca parametrii nu iau niciodata valoarea 0.

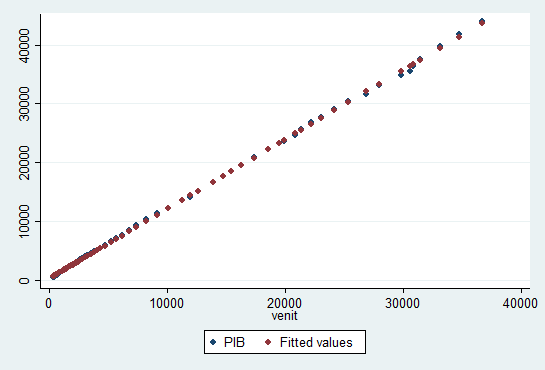
Norul de puncte care analizeaza legatura dintre PIB si nivelul veniturilor este prezentat in graficul urmator:

2.2. Variabilele folosite

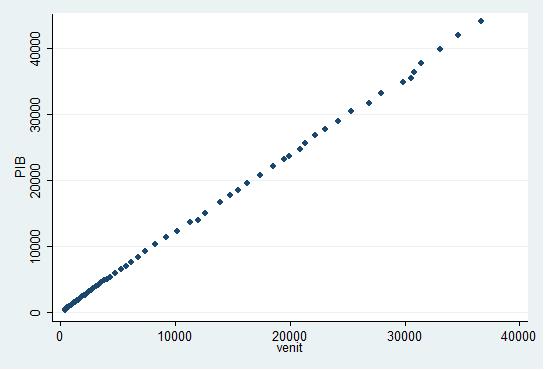
. codebook PIB venit

PIB (unlabeled)

type: numeric (float)

range: [449,44007] units: 1

unique values: 78 missing .: 0/78

mean: 11227.7

std. dev: 12594.3

percentiles: 10% 25% 50% 75% 90%

venit (unlabeled)

type: numeric (float)

range: [373,36632] units: 1

unique values: 78 missing .: 0/78

mean: 9322.58

std. dev: 10620.3

percentiles: 10% 25% 50% 75% 90%

Studiul variabilelor ne arata ca acestea sunt cantitative si ca nu exista date lipsa. Acest lucru arata ca variabilele pot fi folosite in regresie, deoarece la o prima vedere nu prezinta erori.

2.3. Testarea parametrilor

Testul White

PIB = 362.0339 * indicepret

Asadar, atunci cand pretul creste cu 1 miliard dolari, PIB-ul la nivelul SUA creste cu 362.0339 miliarde dolari.

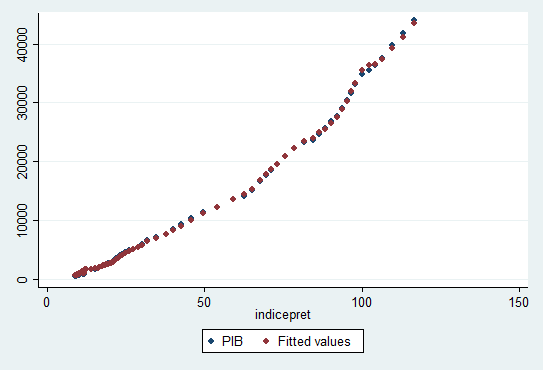
Norul de puncte care analizeaza legatura dintre PIB si nivelul preturilor este prezentat in graficul urmator:

3.2. Variabilele folosite

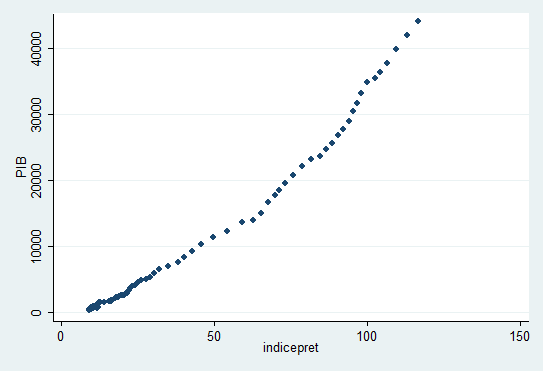
. codebook PIB indicepret

PIB (unlabeled)

type: numeric (float)

range: [449,44007] units: 1

unique values: 78 missing .: 0/78

mean: 11227.7

std. dev: 12594.3

percentiles: 10% 25% 50% 75% 90%

indicepret (unlabeled)

type: numeric (float)

range: [8.91,116.568] units: .001

unique values: 78 missing .: 0/78

mean: 43.1065

std. dev: 34.3363

percentiles: 10% 25% 50% 75% 90%

Studiul variabilelor ne arata ca acestea sunt cantitative si ca nu exista date lipsa. Acest lucru arata ca variabilele pot fi folosite in regresie, deoarece la o prima vedere nu prezinta erori.

3.3. Testarea parametrilor

. testparm indicepret

( 1) indicepret = 0

F( 1, 76) = 2872.07

Prob > F = 0.0000

Intrucat valoarea F este 0, ipoteza nula "parametrul variabilei indicepret este 0" este respinsa, asadar parametrul este diferit de 0.

3.4. Corelarea

. correlate PIB indicepret

(obs=78)

| PIB indice~t

PIB | 1.0000

indicepret | 0.9870 1.0000

Inca o data se demonstreaza corelarea dintre PIB si indicele preturilor. Aceasta corelatie este foarte mare 0.9870, deci factorul considerat poate explica in mare masura variatia variabilei dependente.

3.5. Autocorelarea

Prin aplicarea testului Breusch-Godfrey putem determina existenta unei autocorelari la nivelul modelului:

. estat bgodfrey

Breusch-Godfrey LM test for autocorrelation

lags(p) | chi2 df Prob > chi2

H0: no serial correlation

Avand in vedere ca valoarea ,hi patrat' este 0, ipoteza nula de inexistenta autocorelarii este respinsa. Asadar modelul prezinta o autocorelare.

. estat dwatson

Durbin-Watson d-statistic( 2, 78) = .0368163

Testul Durbin-Watson arata existenta unei autocorelari la nivelul modelului, intrucat valoarea coeficientului este destul de apropiata de 0, ceea ce arata o corelare directa intre erori.

3.6. Analiza reziduurilor si predictiilor

3.6.1. Media reziduurilor

. ttest rpret==0

Testul White

. estat imtest,white

White's test for Ho: homoskedasticity

against Ha: unrestricted heteroskedasticity

chi2(2) = 34.21

Prob > chi2 = 0.0000

Cameron & Trivedi's decomposition of IM-test

Source | chi2 df p

Heteroskedasticity | 34.21 2 0.0000

Skewness | 18.18 1 0.0000

Kurtosis | 1.06 1 0.3037

Total | 53.44 4 0.0000

H₀: modelul este homoscedastic

H₁: modelul nu este homoscedastic

λ_calc = 34.21

λ_tab = 5.99 (sunt 2 grade de libertate)

λ_calc > λ_tab => H₀ se respinge, deci modelul nu este homoscedastic.

Din cele observate si testate pana acum se observa ca acest model este heteroscedastic, erorile sunt autocorelate, nu urmeaza legea normala, iar media acestora este semnificativ diferita de 0. Asadar renuntam la acest model si in continuare ne propunem sa gasim un model care sa explice variatia produsului intern brut in functie de amandoi factorii prezentati pana acum : veniturile si preturile.

4. Modelul liniar multifactorial: PIB in functie de nivelul veniturilor si al preturilor

4.1. Analiza regresiei

. regress PIB venit indicepret

Source | SS df MS Number of obs = 78

F( 2, 75) = .

Model | 1.2210e+10 2 6.1049e+09 Prob > F = 0.0000

Residual | 3594817.54 75 47930.9005 R-squared = 0.9997

Adj R-squared = 0.9997

Total | 1.2213e+10 77 158616055 Root MSE = 218.93

PIB | Coef. Std. Err. t P>|t| [95% Conf. Interval]

venit | 1.157639 .0143654 80.59 0.000 1.129022 1.186257

indicepret | 8.792613 4.443268 1.98 0.052 -.0588302 17.64406

_cons | 56.47864 68.00137 0.83 0.409 -78.98703 191.9443

La fel ca in cazul modelelor unifactoriale, si aici se observa o puternica informatie detinuta de cei 2 factori. Asadar variatia modelului este 1.2210e+10 , net mai mare decat cea reziduala, ceea ce conduce la un R patrat foarte mare de 0.9997. Aceasta inseamna ca informatia explicata de factori este in proportie de 99.97%.

De asemenea, o prima analiza a modelului il anunta valid, astfel ca valoarea F este 0, ceea ce inseamna ca modelul este reprezentativ si poate conduce la viitoare prognoze.

Forma modelului este data de coeficientii parametrilor:

PIB = + 1.157639 * venit + 8.792613* indicepret +

Asadar, la o modificare cu 1 miliard dolari a veniturilor, PIB-ul va creste cu 1.15 miliarde dolari, iar la o modificare a preturilor cu 1 miliard dolari, PIB-ul va creste cu 8.79 miliarde dolari.

P>|t| arata ca parametrii coeficientilor sunt valizi, ca factorii alesi sun valabili, in sensul ca coeficientii corespunzatori acestora nu pot lua valoarea 0. Acest lucru ne arata si intervalul de incredere, care nu il cuprinde pe 0.

4.2. Corelarea

. correlate PIB venit indicepret

(obs=78)

| PIB venit indice~t

PIB | 1.0000

venit | 0.9998 1.0000

indicepret | 0.9870 0.9865 1.0000

Din analiza tabelului de corelatii se observa puternica corelatie dintre variabila dependenta si fiecare factor, dar si puternica corelatie dintre factori, ceea ce slabeste din validitatea modelului regresional.

4.2.1. Eliminarea fenomenului de corelare a factorilor

Pentru a elimina fenomenul de corelare a factorilor se va realiza analiza componentelor principale, rezultand doua variabile noi, in functie de cele anterior avute. Astfel:

. pca venit indicepret

Principal components/correlation Number of obs = 78

Number of comp. = 2

Trace = 2

Rotation: (unrotated = principal) Rho = 1.0000

Component | Eigenvalue Difference Proportion Cumulative

Comp1 | 1.98654 1.97308 0.9933 0.9933

Comp2 | .0134622 . 0.0067 1.0000

Principal components (eigenvectors)

Variable | Comp1 Comp2 | Unexplained

venit | 0.7071 0.7071 | 0

indicepret | 0.7071 -0.7071 | 0

Noile componente ale modelului vor fi:

F1 = 0.7071*venit + 0.7071*indicepret

F2 = 0.7071*venit - 0.7071*indicepret

4.2.2. Regresia in functie de factorii F1 si F2

. regress PIB f1 f2

Source | SS df MS Number of obs = 78

F( 2, 75) = .

Model | 1.2210e+10 2 6.1049e+09 Prob > F = 0.0000

Residual | 3594812.52 75 47930.8336 R-squared = 0.9997

Adj R-squared = 0.9997

Total | 1.2213e+10 77 158616055 Root MSE = 218.93

PIB | Coef. Std. Err. t P>|t| [95% Conf. Interval]

f1 | 7.036149 3.131896 2.25 0.028 .7970917 13.27521

f2 | -5.398985 3.151939 -1.71 0.091 -11.67797 .8799989

_cons | 56.47501 68.00173 0.83 0.409 -78.99139 191.9414

Se observa ca si in acest caz se mentin valorile ridicate ale variantei explicite cat si a R. Asadar si acest model este reprezentativ si trece de primele teste.

Forma modelului este:

PIB = 56.47501 + *f1 *f2

Inlocuind cu valorile initiale ale factorilor vom avea:

PIB = 56.47501 + 1.1576378 * venit + 1.1576378 * indicepret

4.3. Corelatia partiala

. pcorr PIB venit indicepret

(obs=78)

Partial correlation of PIB with

Variable | Corr. Sig.

venit | 0.9943 0.000

indicepret | 0.2228 0.052

Daca se ia in considerare doar actiunea factorului (venit), celalalt factor ramanand constant, atunci rezulta ca acesta influenteaza variabila Y in proportie de 0.9943.

Daca se ia in considerare doar actiunea factorului (indicepret), celalalt factor ramanand constant, atunci rezulta ca acesta influenteaza variabila Y in proportie de 0.2228.

4.4. Autocorelarea erorilor

. estat dwatson

Durbin-Watson d-statistic( 3, 78) = .6110033

Testul Durbin-Watson arata existenta unei autocorelari la nivelul modelului, intrucat valoarea coeficientului este destul de apropiata de 0, ceea ce arata o corelare directa intre erori.

. estat bgodfrey

Breusch-Godfrey LM test for autocorrelation

lags(p) | chi2 df Prob > chi2

H0: no serial correlation

Avand in vedere ca valoarea ,hi patrat' este 0, ipoteza nula de inexistenta autocorelarii este respinsa. Asadar modelul prezinta o autocorelare.

4.4.1. Eliminarea fenomenului de autocorelare

Pentru a corecta autocorelarea erorilor cu ajutorul STATA se va rula testul Prais-Winston, specificandu-se de asemenea optiunea Cochran-Orcutt.

Datele obtinute vor fi vizibil diferite fata de cele originale:

. prais PIB f1 f2 ,corc

Iteration 0: rho = 0.0000

Iteration 1: rho = 0.7081

Iteration 2: rho = 0.7167

Iteration 3: rho = 0.7181

Iteration 4: rho = 0.7183

Iteration 5: rho = 0.7183

Iteration 6: rho = 0.7183

Iteration 7: rho = 0.7183

Iteration 8: rho = 0.7183

Cochrane-Orcutt AR(1) regression -- iterated estimates

Source | SS df MS Number of obs = 77

F( 2, 74) =22850.00

Model | 1.1755e+09 2 587761035 Prob > F = 0.0000

Residual | 1903471.11 74 25722.5825 R-squared = 0.9984

Adj R-squared = 0.9983

Total | 1.1774e+09 76 15492441.3 Root MSE = 160.38

PIB | Coef. Std. Err. t P>|t| [95% Conf. Interval]

f1 | 9.545685 6.797692 1.40 0.164 -3.999012 23.09038

f2 | -7.921125 6.839497 -1.16 0.251 -21.54912 5.706871

_cons | 6.719343 164.2768 0.04 0.967 -320.6093 334.048

rho | .7183342

Durbin-Watson statistic (original) 0.611004

Durbin-Watson statistic (transformed) 1.717177

Observam ca valoarea coeficinetului Durbin-Watson este peste 1 ceea ce inseamna ca nu mai exista o autocorelare a erorilor. Se observa ca modelul este valid atat din punct de vedere al informatiei esplicate de factori, cat si din punct de vedere al posibilitatii de predictie (F=0). De asemenea, coeficientii modelului sunt diferiti de 0.

4.5. Testarea parametrilor

. testparm f1 f2

( 1) f1 = 0

( 2) f2 = 0

F( 2, 75) = 1.3e+05

Prob > F = 0.0000 => parametrii sunt diferiti de 0

4.6. Legatura intre reziduuri si variabilele factor

Reziduurile nu trebuie sa fie corelate cu factorii

. correlate venit indicepret rmodel

(obs=78)

| venit indice~t rmodel

venit | 1.0000

indicepret | 0.9865 1.0000

rmodel | 0.0000 -0.0000 1.0000

Din tabelul de mai sus se observa ca variabilele factor (venitul si indicele preturilor) nu se coreleaza cu reziduurile.

4.7. Analiza reziduurilor si predictiilor

4.7.1. Media reziduurilor

. ttest rmodel==0

One-sample t test

Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]

rmodel | 78 3.89e-07 24.46501 216.0691 -48.71606 48.71607

mean = mean(rmodel) t = 0.0000

Ho: mean = 0 degrees of freedom = 77

Ha: mean < 0 Ha: mean != 0 Ha: mean > 0

Pr(T < t) = 0.5000 Pr(|T| > |t|) = 1.0000 Pr(T > t) = 0.5000

Testarea mediei rezidurilor egala cu 0 arata ca aceasta este egala cu 0.

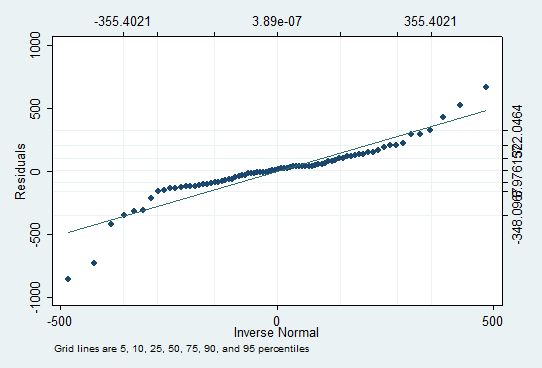
4.7.2. Distributia erorilor fata de model

Din acest grafic se observa ca erorile sunt normal distribuite.

4.7.3. Testarea normalitatii reziduurilor

PIB-ul in functie de variatia preturilor:

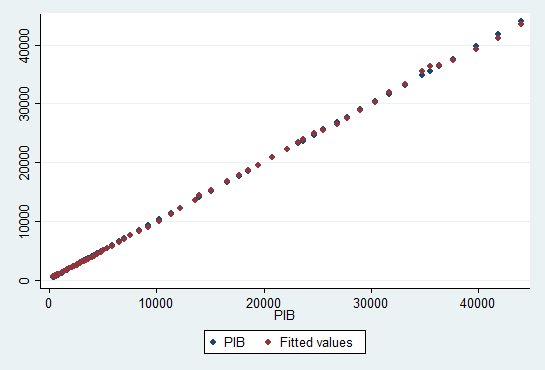
PIB-ul prezis de modelul multifactorial, luand in considerare atat variatia veniturilor cat si variatia preturilor:

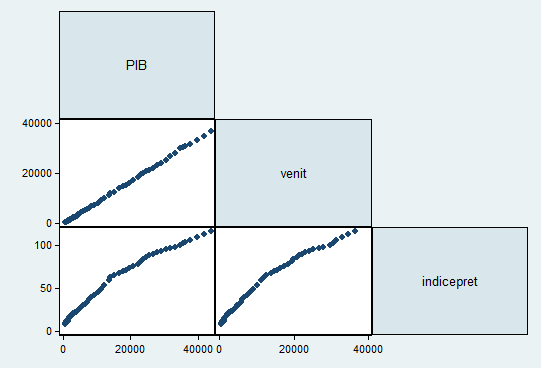
Comparand variantele celor doua variabile : PIB-ul in valori reale si PIB-ul in valori prezise se observa ca acestea au variantele egale:

. sdtest PIB==pmodel

Variance ratio test

Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]

PIB | 78 11227.68 1426.022 12594.29 8388.107 14067.25

pmodel | 78 11227.68 1425.812 12592.43 8388.525 14066.83

combined | 156 11227.68 1005.018 12552.67 9242.38 13212.98

ratio = sd(PIB) / sd(pmodel) f = 1.0003

Ho: ratio = 1 degrees of freedom = 77, 77

Ha: ratio < 1 Ha: ratio != 1 Ha: ratio > 1

Pr(F < f) = 0.5005 2*Pr(F > f) = 0.9990 Pr(F > f) = 0.4995

5. Concluzii

Analizand validitatea modelelor se observa ca acestea nu trec toate testele necesitand astfel diferite ajustari. Este clar insa ca intr-o economie, variatia PIB-ului este determinata de variatia nivelului veniturilor si de variatia nivelului preturilor. Asadar, variabila independenta, dupa cum ne arata si testele si modelele depinde in mare masura de cei doi factori analizati.

Modelul PIB-ului in functie de venit si pret poate arata astfel:

Document Info

Accesari: 28381
Apreciat:

Comenteaza documentul:

Nu esti inregistrat
Trebuie sa fii utilizator inregistrat pentru a putea comenta

Creaza cont nou

A fost util?

Daca documentul a fost util si crezi ca merita
sa adaugi un link catre el la tine in site

Copiaza codul:
in pagina web a site-ului tau.

eCoduri.com - coduri postale, contabile, CAEN sau bancare

Politica de confidentialitate | Termenii si conditii de utilizare