SPATIU METRIC

Daca in cadrul structurii de spatiu topologice densitatea elementelor putea fi data numai cu ajutorul vecinatatilor fara a se putea stabili "distanta" dintre acestea, in cadrul structurii de spatiu metric se va putea s 16416w2216q tabili si aceasta "distanta".

Definitia 1. (Notiunea de distanta sau metrica)

Fie o multime oarecare si aplicatia .

Daca:

1^o oricare ar fi si daca si numai daca

2^o , oricare ar fi

3^o oricare ar fi (inegalitatea triunghiului),

atunci aplicatia este distanta sau metrica pe multimea .

Cupletul , poarta denumirea de spatiu metric.

Propozitia 1. Orice multime poate fi metrizabila (inzestrata cu structura de spatiu metric).

Demonstratie:

Pentru a arata acesta afirmatie este suficient sa se construiasca pe o aplicatie , care sa verifice axiomele din definitia 1. Intr-adevar daca se considera:

este o distanta pe , deoarece verifica toate cele trei axiome.

1^o Axioma 1 este evidenta din modul de constructie

2^o Pentru orice | rezulta ca = 1 =

3^o Pentru cazul 3 pot exista mai multe posibilitati:

sau sau sau etc.

Pentru avem

rezulta ca:

In mod analog se demonstreaza axioma 3 pentru celelalte cazuri, astfel rezulta ca orice multime poate fi metrizabila.

Observatia 1. Pe o multime E pot fi considerate mai multe metrici care au proprietatea ca pe acea multime una masoara mai fin decat cealalta.

Exemple:

Aplicatiile definite mai jos sunt metrici sau distante pe multimile specificate:

a)          este metrica pe i

b)          unde , este metrica pe i²

c)          unde , este metrica pe i³

d)  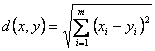        unde , este metrica pe i^m.

Aceste distante se numesc distante euclidiene.

Definitia 2. Fie spatiu numeric. Multimile

si

se numesc sferele deschise respectiv inchise ale spatiului metric .

Observatia 2.

a) metrica euclidiana, atunci

si

b) si d metrica euclidiana, atunci

si se numeste discul plan deschis, iar

si se numeste discul plan inchis.

c)

si se numeste sfera deschisa din i³

si se numeste sfera inchisa din i³.

Propozitia 2. Orice sptiu metric este un spatiu topologic. Reciproca nu este in general adevarata.

Demonstratie:

Se arata ca formeaza o topologie. Aceasta topologie mai poarta denumirea si de topologie metrica.

Pentru a arata ca este o topologie se arata ca sunt multimi deschise, pentru orice fixat si orice .

Indicatie: Se arata ca (interior).

In mod analog ca mai sus se arata ca daca (sunt multimi deschise) atunci .

Daca pentru orice avem de unde rezulta ca intr-adevar este o topologie.

4. NORMA. SPATIU VECTORIAL NORMAT

Definitia 1:

Fie un spatiu vectorial si o aplicatie. Daca:

> 0, pentru orice ; si = 0, daca . ( este elementul neutru in raport cu adunarea in spatiu vectorial )

, pentru orice

, pentru orice ,

Atunci aplicatia este o norma pe .

Cupletul se numeste spatiu vectorial normat, iar norma , mai are si urmatoarea notatie: .

Propozitia 1. Orice norma defineste o distanta.

Demonstratie: Fie un spatiu vectorial normat, iar norma j mai are si urmatoarea notatie .

Aplicatia este o distanta (metrica) pe multimea E. Pentru aceasta trebuie verificate axiomele metricii, tinand cont ca axiomele normei sunt verificate.

1^o pentru orice si rezulta . Intr-adevar

pentru orice . Dar daca si numai daca si rezulta . Dar daca si numai daca .

2^o Trebuie aratat ca . Intr-adevar

3^o Trebuie aratat ca oricare ar fi . Intr-adevar

Astfel am demonstrat ca orice norma defineste o distanta.

Observatia 1. Tinand cont de propozitia anterioara, orice spatiu vectorial normat este si un spatiu metric dar reciproca nu este in general valabila.

Intr-un spatiu vectorial normat se poate opera cu elementele si se pot crea vecinatati in care se poate determina precis densitatea elementelor prin masurarea distantei dintre ele, dar intr-o astfel de structura nu se poate defini notiunea de directie, deci de unghi. Aceasta directie poate fi stabilita cu ajutorul notiunii de produs scalar.

Definitia 2:

Fie un spatiu vectorial normat peste campul si aplicatia , daca:

1. , oricare ar fi

2. , oricare ar fi

3. , oricare ar fi

, oricare ar fi , si

, daca si numai daca .

Atunci aplicatia se numeste produs scalar pe spatiul vectorial .

Produsul scalar se noteaza si astfel .

Observatia 2: Fie un spatiu vectorial. Daca acest spatiu vectorial este inzestrat cu un produs scalar, atunci poarta denumirea de spatiu prehilbertian.

Propozitia 2. Fie E spatiu vectorial si un produs scalar. (E un spatiu prehilbertian), atunci au loc urmatoarele relatii:

1^o

2^o

3^o (inegalitatea Cauchy-Buniakovski-Schwarz).

Demonstratie:

1^o Tinand cont de punctul 1 din definitia 2 rezulta

2^o

3^o Fie . Atunci conform definitiei produsului scalar se poate scrie ca:

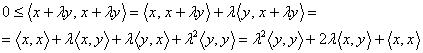
Deci pentru orice avem:

(trinom de gradul doi in ) unde . Din proprietatile trinomului de gradul 2 este evident ca . Asadar

Propozitia 3. Oprice produs scalar defineste o norma.

Intr-adevar daca se considera aplicatia:

atunci aceasta aplicatie este o norma pe multimea E. Tinand cont ca proprietatile produsului scalar sunt verificate, trebuie aratat ca aceasta aplicatie verifica proprietatile normei.

1^o , pentru orice si rezulta

Intr-adevar , pentru orice rezulta pentru orice .

2^o Trebuie aratat ca , pentru orice .

Intr-adevar .

3^o Trebuie aratat ca .

Intr-adevar

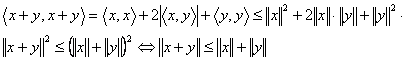
Exemplu: Fie . Sa se arate ca aplicatia:

a)      este un produs scalar pe

b)      Daca este un produs scalar.

Definitia 3. Fie un spatiu topologic. Acest spatiu topologic se numeste topologic separat daca pentru orice cu exista si astfel incat .

Spatiu topologic separat prezinta o importanta deosebita deoarece numai intr-un astfel de spatiu topologic, atunci cand limita exista, ea este unica.

Notiunea de convergenta este bine definita intr-un spatiu topologic separat.

Propozitia 4. Orice spatiu vectorial normat este un spatiu topologic separat.

Demonstratie: Fie spatiu vectorial normat.

Fie arbitrare. Se considera .

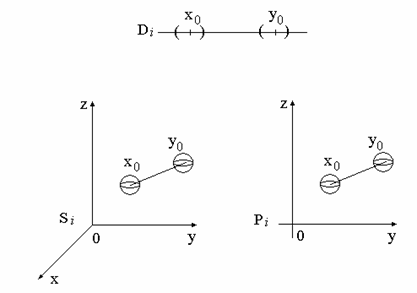
Fie sferele:

.

Aceste multimi sunt vecinatati ale lui respectiv in topologia metrica.

Dar este evident ca

SIRURI IN SPATII TOPOLOGICE, SPATII METRICE,

SPATII VECTORIALE NORMATE

Definitia 1: Fie o multime oarecare si , o functie, poarta denumirea de termenul general al sirului, generat de functia in multimea , iar sirul de elemente din multimea , ce are acest termen general se mai noteaza si astfel:

1. , (nu intereseaza forma termenilor sirului)

2. , (sirul este considerat ca o multime; intereseaza elementele lui).

Observatia 1:

a)      Se observa din defin itia anterioara ca sirul este multimea valorilor unei functii oarecare f, dar care are domeniul de definitie ¥,

b)      Natura elementelor multimii E, da tipul sirului. Astfel:

sir de numere reale

£ sirul este de numere complexe

sir de elemente din

sirul functiilor

c)      Pentru a putea fi facut un studiu complet al sirurilor, multimea E trebuie sa fie organizata cu structura de spatiu vectorial normat.

Dar studiul sirurilor mai poate fi efectuat si daca E este inzestrata cu structura de spatiu metric sau de spatiu topologic (nu se pot face operatii cu siruri).

Problema care se pune in legatura cu sirurile, dupa cum se stie este monotonia, marginirea si convergenta acestora.

Monotonia:

Daca multimea este o multime ordonata, atunci sirul si este monoton.

Monotonia sirurilor reale este:

a) - se spune ca sirul este strict crescator.

b) - se spune ca sirul este crescator.

c) - se spune ca sirul este strict descrescator.

d) - se spune ca sirul este descrescator.

Marginirea:

Notiunea de marginire a unui sir este posibila daca multimea este un spatiu metric cel putin. Cum sirul este de fapt multimea , definitia marginirii este urmatoarea:

Definitie:

Fie , un spatiu metric, sirul cu este marginit daca exista fixat si , astfel incat , pentru orice , .

Cum orice sir poate fi considerat ca o multime, folosind notatia , toate afirmatiile legate de multimi marginite sunt valabile si pentru siruri.

Daca , atunci sirul are urmatoarea forma:

unde sunt siruri de numere reale care se mai numesc proiectiile sirului .

Deoarece un sir este o multime, propozitia referitoare la marginirea multimilor din se transpune si la marginirea sirurilor astfel:

Propozitie: Fie un sir de elemente din ; acest sir este marginit daca si numai daca fiecare proiectie a sa este un sir marginit.

Convergenta:

Notiunea de convergenta a unui sir este posibila daca multimea este inzestrata cu structura de spatiu topologic, spatiu metric si spatiu vectorial normat.

Convergenta in spatiu topologic: Fie un spatiu topologic si , un sir din acest spatiu. Se spune ca sirul este convergent in topologia daca exista astfel incat pentru orice o vecinatate a punctului , exista un rang astfel incat pentru orice .

Convergenta in spatiu metric: Fie , un spatiu metric si un sir din acest spatiu. Se spune ca este convergent in metrica daca exista astfel incat oricare ar fi exista astfel incat pentru orice

6. SIRURI CAUCHY

Notiunea de sir Cauchy sau fundamental, este o notiune utila in studiul convergentei sirurilor atunci cand limita este greu sau imposibil de calculat.

Definitia sirului Cauchy: Fie , un spatiu metric si un sir de elemente din acest spatiu. Se spune ca sirul este un sir Cauchy sau sir fundamental, daca si numai daca pentru orice exista astfel incat oricare ar fi rezulta ca .

Criteriul de convergenta al lui Cauchy pentru siruri: Intr-un spatiu metric complet un sir este convergent daca si numai daca este un sir Cauchy.

Un sir de numere: este convergent daca si numai daca pentru orice numar exista un numar astfel incat oricare ar fi si orice numar intreg sa avem | < .

Demonstratie:

Conditia este necesara:

Intradevar, sirul, fiind convergent, are o limita si deci pentru oricare ar fi , exista , astfel incat pentru sa avem | deci si pentru , deoarece .

In egalitatea:

avem:

Conditia este asadar necesara.

Conditia este suficienta:

Sa dam lui valoarea fixa . Conform ipotezei: |, cu deci cu exceptia termenilor , toti ceilalti termeni (= 1, 2,.) se afla in intervalul .

Sa presupunem ca este limita superioara si , limita inferioara, , rezulta de aici ca si se gasesc in acest interval, deci:

,

fiind arbitrar, iar si sunt fixe, diferenta lor nu poate fi arbitrar de mica daca =, iar sirul este convergent.

Exemplu: Avem sirul:

Este convergent

,

deoarece sumele s.a.m.d. sunt toate negative.

Rezolvare:

----- ----- -----

5y = 5