Relatia relativista dintre energie si impuls. Cuadrivectorul energie-impuls
Din formulele 
si 
obtinem, prin eliminarea masei 
:
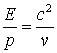(4.124)
Eliminand
apoi viteza 
intre (4.124) si (4.120), 151i87b obtinem:
(4.125)
de unde
(4.126)
Am obtinut
astfel, relatia relativista dintre energie si impuls.
Pentru particule cu masa de repaus nula (
), ca de
exemplu fotonii, relatia relativista dintre energie si impuls are
forma:
(4.127)
Cuadrivectorul impuls (4.113) este:
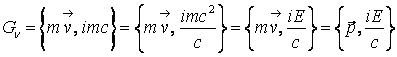(4.128)
si poarta numele de cuadrivectorul energie-impuls. Stim ca patratul oricarui cuadrivector este invariant fata de transformarile Lorentz:
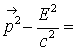invariant (4.129)
Daca particula
se afla
in repaus fata de un sistem de referinta inertial oarecare,
atunci 
, deci in
acest caz:
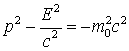(4.130)
Astfel,
cuadrivectorul 
are componentele:
(4.131)
care se transforma dupa formulele generale (4.73) si (4.74)
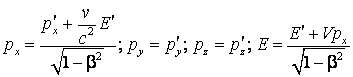(4.132)
Daca in 
particula se afla in
repaus, 
, si avem:
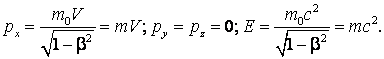(4.133)
Exemplul 7
Sa se calculeze raportul dintre masa de repaus si masa de miscare a unei particule relativiste in functie de:
a) energia totala 
si impulsul 
;
b) energia cinetica 
si impulsul ;
c) Sa se exprime raportul 
in functie de impulsul si energia cinetica .
Rezolvare
a) Se exprima din (4.120) si 
(4.126) , apoi se face raportul:
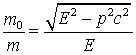
b) Din (4.131) obtinem:
Identificand cu (4.126)
rezulta:
Din (4.126) si (4.122) obtinem:
Impartind ultimele doua ecuatii, obtinem:
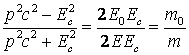
c) Din (4.120) obtinem:
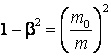
si
inlocuind raportul 
obtinut la punctul b), obtinem:
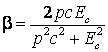
Exemplul 8
Cuadrivectorul energie-impuls al unei particule relativiste are forma:
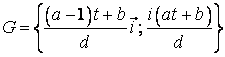(4.134)
unde 
este timpul, iar 
si 
sunt constante in raport cu timpul, 
este versorul axei Ox, iar 
este numarul complex. Cunoscand norma
cuadrivectorului 
, sa se
determine:
a) Masa de repaus a particulei;
b) Viteza particulei la momentul ;
c) Relatia dintre parametrii 
si la orice moment de timp .
Rezolvare
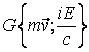, unde 
; 
, de unde
rezulta:
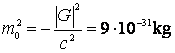
b) Identificand (4.134) cu 
si rezolvand
sistemul celor doua ecuatii, se obtine:
c)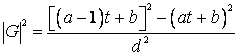 
reprezinta
expresia normei cuadrivectorului energie-impuls (4.134), de unde rezulta
ecuatia:
Din conditia pentru
determinantul ecuatiei, 
, obtinem:
Exemplul 9
O placa plana omogena de
masa 
are forma
unui patrat de latura 
, ambele
marimi fiind masurate in sistemul propriu. Sistemul de referinta se deplaseaza cu viteza 
in raport cu un referential 
astfel ca 
, iar placa
se deplaseaza uniform fata de cu viteza 
pe directia 
. Se cer:
a) Marimea diagonalei placii si unghiul format de diagonala cu directia de
miscare, in raport cu ;
b) Densitatea superficiala 
a placii in raport cu ;
c) Impulsul si energia cinetica in raport cu .
d) Durata unui proces ce se desfasoara pe placa, determinata de un
observator legat de , daca un
observator legat de determina o durata 
.
Se cunosc viteza luminii in
vid 
si densitatea de energie in sistemul propriu 
.
Rezolvare
a) 
.
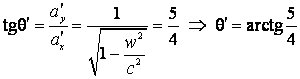
b)
c);
.
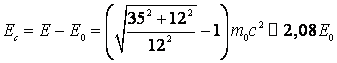
d)
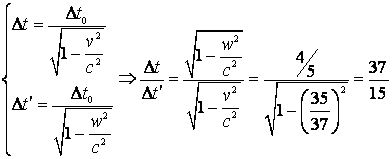
Exemplul 10
Sa se calculeze timpul
propriu al unei particule care a fost accelerata un timp cu acceleratia 
.
Rezovare
Consirderam ca la momentul 
de asemenea 
. Prin integrare
se obtine:
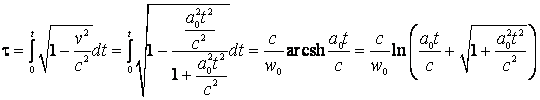
Daca
, neglijand
1fata de 
, se
obtine:
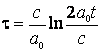(4.135)
Formula (4.135) ar putea
explica, cel putin in parte, de ce un calator care se deplaseaza uniform
accelerat ar avea, la intoarcerea pe Pamant, o varsta mai mica decat un frate
geaman ramas pe Pamant. Se observa ca o data cu cresterea lui creste si 
, insa
acesta creste mult mai incet. De exemplu, pentru 
si 
ani (timpul
masurat de geamanul de pe Pamant) din (4.135) se obtine 
ani, care reprezinta cat timp s-a adaugat la
"varsta" geamanului care a calatorit prin spatiu.
Exemplul 11
Se considera o particula cu
masa de repaus 
sub actiunea unei forte constante 
.
a) Sa se determine expresia lucrului mecanic efectuat de aceasta forta,
astfel incat particula plecand din repaus intr-o miscare rectilinie sa ajunga
la viteza 
dupa un timp .
b) Sa se deduca expresia relativista a energiei cinetice. Discutie
Rezolvare
(4.136)
La momentul : 
, 
si 
.
La momentul impulsul este , si expresia
(4.136) devine:
(4.137)
(4.138)
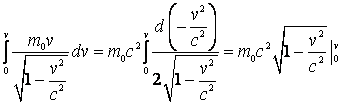
Inlocuind (4.137) in (4.136), obtinem:
b) Din teorema energiei cinetice:
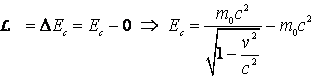(4.139)
Se observa ca energia cinetica este
diferenta intre valorile unei functii de viteza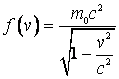 
pentru valorile argumentului 
, respectiv
.
Apare normal ca cei doi termeni din
(4.139) sa reprezinte energia asociata particulei aflate in miscare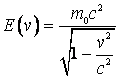 
, respectiv
energia asociata particulei aflata in repaus, 
. Aceasta
din urma se mai numeste si energia proprie
a particulei de masa .
|
