Aplicatii ale seriilor
Formula lui ![]() etc..
etc..
Exemple:
1). 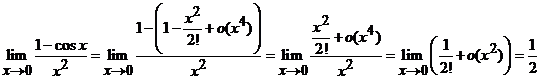 .
.
2). 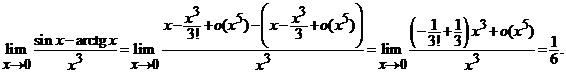
3). 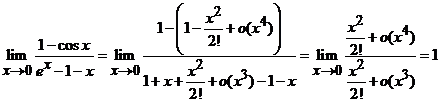 .
.
4).
Calculati integrala ![]() cu o precizie mai
mica decat
cu o precizie mai
mica decat ![]() . Avem
. Avem
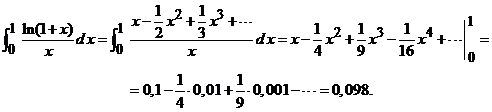
. Folosind dezvoltarile in serie de
puteri (serie
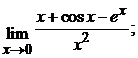
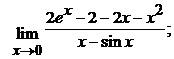
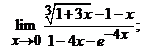
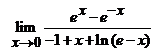 .
.
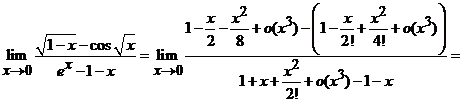
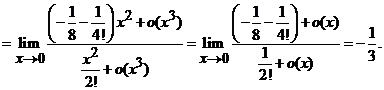
. Fie ![]() , definita astfel
, definita astfel 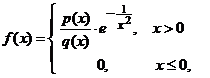 atunci
atunci ![]() .
.
Demonstratie. Aratam ca ![]() este functie continua pe
este functie continua pe ![]() . Intr-adevar, prin definitie, functia
. Intr-adevar, prin definitie, functia ![]() este continua
pentru orice
este continua
pentru orice ![]() . In punctul
. In punctul ![]() putem scrie
putem scrie
![]()
![]() si
si 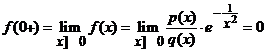
si deci ![]() este continua pe
este continua pe ![]() .
.
Pentru ![]() avem
avem 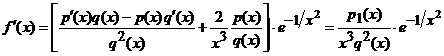 .
.
Daca ![]() atunci
atunci ![]() . Deci
. Deci
![]()
![]() .
.
Asadar, derivata in ![]() exista si
este egala cu zero. Rezulta ca
exista si
este egala cu zero. Rezulta ca ![]() este
diferentiabila pe
este
diferentiabila pe ![]() si derivata
si derivata ![]() are aceeasi
forma cu
are aceeasi
forma cu ![]() . Prin recurenta deducem ca
. Prin recurenta deducem ca ![]() este
diferentiabila si are aceeasi forma cu
este
diferentiabila si are aceeasi forma cu ![]() , deci
, deci ![]() .
.
De exemplu, functia 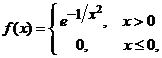 este de clasa
este de clasa ![]() pe
pe ![]() .
.
|