CALCULUL SI CONSTRUCTIA CUTIEI DE VITEZE

CALCULUL SI CONSTRUCTIA CUTIEI DE VITEZE

Cutiile de viteze actuale s-au diferentiat atât ca principiu de functionare cât si ca mod de deservire. Din acest punct de vedere trebuie sa se faca distinctie între agregatul de lucru ca transformator de cuplu si dispozitivul sau sistemul de actionare prin care se alege regimul optim de functionare al cutiei de viteze.

Rezistentele la înaintarea autovehiculului variaza mult în functie de conditiile de concrete de deplasare si corespunzator acestora trebuie sa se schimbe si forta de tractiune la rotile motoare. Marea majoritate a automobilelor actuale sunt echipate cu motoare cu ardere interna, a caror particularitate consta în faptul ca puterea maxima este dezvoltata la turatii foarte ridicate. Automobilul necesita puteri mari si la viteze mici, care însa nu pot fi asigurate de motor datorita valorii relativ ridicate a turatiei minime stabile de functionare a acestuia. În consecinta, automobilul trebuie sa fie înzestrat cu un dispozitiv care sa permita schimbarea turatiei si momentul rotilor motoare în timpul mersului si sa asigure utilizarea integrala a puterii motorului la toate regimurile de functionare. Acestui scop îi serveste cutia de viteze, care îndeplineste functia unui variator de cuplu si turatie în transmisia autovehiculului, asigurând totodata posibilitatea mersului înapoi si functionarea motorului la regim de mers încet, în gol, atunci când automobilul sta pe loc.

7.1. Alegerea tipului constructiv

- inversor al sensului de mers al automobilului:

- cum sensul de rotatie al motorului este prin conceptie unic, cutia de viteze contine elemente a caror dispunere permite, când este necesara inversarea sensului de rotatie a arborelui de iesire;

- decupleaza motorul termic de rotile motoare (punct mort):

- deoarece prin conceptie, ambreiajul nu poate fi decuplat decât temporar, pentru situatiile în care este necesara functionarea motorului cu automobilul imobilizat, lantul cinematic este întrerupt prin aducerea elementelor mobile de cuplare într-o pozitie neutra.

În scopul asigurarii unei bune adaptabilitati a automobilului conditiilor concrete în care are loc deplasarea, cutia de viteze trebuie sa raspunda la o serie de cerinte, prin care:

- sa aiba posibilitatea realizarii unui numar cât mai mare de rapoarte de transmitere, iar marimea lor sa fie determinata în asa fel încât sa asigure o utilizare rationala a puterii în conditiile unor performante economice, dinamice si de poluare optime pentru caracteristica motorului cu care se conlucreaza;

- constructia sa fie simpla, robusta, usoara, iar manevrarea sa fie simpla, precisa si comoda;

- în exploatare sa prezinte siguranta si întretinere usoara iar manevrarea sa fie simpla, precisa si comoda;

- sa prezinte o gama larga de utilizare.

Dupa modul de modificare a raportului de transmitere, cutiile de viteze pot fi cu variatia în trepte, cu variatia continua (progresiva), sau combinate.

Nr. poz.

Denumirea elementului

Simbol

Indicatia de adoptare

Standarde aferente

Numarul de dinti:

- la pinion

- la roata

z₁

z'₂

z'₁= z₁ i_cv1=50

Modulul normal

m_n

STAS 822-82

Unghiul de înclinare de divizare

b

Unghiul de presiune de referinta normal

a_n

a_n

STAS 821-82

Coeficientul normal al capului de referinta

h^*_an

h^*_an=1

STAS 821-82

Coeficientul normal al jocului de referinta la capul dintelui

c^*_n

c^*_n=0,25

STAS 821-82

Coiefifientul normal al adâncimii de flancare a capului dintelui

D _aFn

Recomandari în STAS 821+82

Se foloseste ca data initiala numai la danturi flancate

Coieficientul normal al adâncimii de flancare a capului dintelui

Se indica prin tema

Se foloseste ca data initiala numai la danturi flancate

Tabelul 7.3. Calculul elementelor geometrice

În tabelul 7.4. sunt prezentate valorile obtinute în calculul geometric si cinematic pentru fiecare treapta de viteza.

Dupa ce s-a adoptat numarul de dinti ai pinionului si rotii corespunzatoare treptei întâi de viteze, se poate calcula distanta dintre axe cu formula:

Angrenajele cutiilor de viteze se verifica prin calculul la încovoierea dintilor si la presiunea de contact.

Tabelul 7.4. Rezultatele calcului de geometric

7.4. Calculul de rezistenta si verificare angrenajelor

de roti dintate

7.4.1. Fortele din angrenaje

Angrenajele cutiilor de viteze se verifica prin calcul la încovoierea dintilor si la presiunea de contact, în conditiile solicitarii sub actiunea sarcinilor de regim si sarcinilor dinamice (sarcini de vârf).

Pentru calculul danturii exista mai multe metode, dintre care cea mai frecvent folosita este metoda lui Lewis.

Aceasta metoda considera ca întregul moment se transmite prin intermediul unui dinte, considerat ca o grinda încastrata si ca asupra dintelui actioneaza forta normala F_n dupa linia de angrenare N-N si este aplicata la vârful dintelui.

Forta nominala se distribuie pe fâsia de contact dintre dintii aflati în angrenare producând ca solicitare principala presiuni specifice de contact.

Functie de momentul de torsiune M_c al arborelui, forta tangentiala se determina cu relatia:

unde: Mc - momentul la arborele rotii conducatoare a angrenajului.

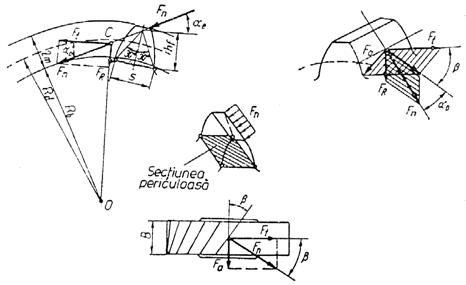
Fig. 7.11. Definirea fortelor din rotile dintate cilindrice cu dantura înclinata

Forta nominala se calculeaza cu formula:

Componenta radiala se calculeaza cu formula:

si solicita dintele la compresiune.

Componenta axiala, care se calculeaza cu formula:

nu determina solicitari asupra dintelui.

În tabelul 7.5. sunt prezentate valorile pentru fortele din angrenaje.

Tabelul 7.5. Valorile pentru fortele din angrenaje.

7.4.2. Calculul de rezistenta la încovoiere

Pe baza ipotezelor aratate, efortul unitar efectiv de încovoiere este dat de relatia:

unde:   - z - numarul de dinti ai rotii conducatoare;

Y

g_ei - coeficient de repartizare al efortului.

Coeficientul de repartizare al efortului tine cont de gradul de acoperire, iar pentru aceasta calculam gradele de acoperire frontal si suplimentar.

Pentru calculul gradului de acoperire frontal se utilizeaza relatia:

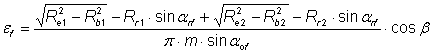
iar pentru gradul de acoperire suplimentar, utilizam relatia:

unde: - R_e1, R_e2 - razele cercurilor de vârf ale rotilor din angrenajul de calculat;

- R_b1, R_b2 - razele cercurilor de baza;

a_rf - unghiul frontal de angrenare;

a_rf - unghiul frontal al profilului de referinta

Pentru calculul la sarcini nominale de regim, la determinarea valorii efective a efortului unitar de încovoiere, momentul de calcul este determinat de momentul maxim al motorului M_max si de raportul de transmitere de la motor la angrenajul calculat prin relatia:

În cazul metodei Lewis, când se considera ca întreg momentul de torsiune se transmite printr-un singur dinte si se neglijeaza efectul compresiunii axiale dat de componenta radiala a fortei normale, rezulta o supradimensionare a danturii. Pentru evitarea supradimensionarii, în calculul de verificare valorile efective ale efortului unitar se compara cu eforturile admisibile la încovoiere pentru materialul utilizat; efortul admisibil de încarcare s_ai se adopta, în mod conventional, cu valori mai ridicate celor definite din conditia de rezistenta la valoarea nominala a momentului:

unde: - c=1,5 - coeficient de siguranta.

La calculul de verificare al rotilor dintate la sarcini dinamice maxime (care apar la cuplarea brusca a ambreiajului si la frânarea brusca cu ambreiajul cuplat), momentul de calcul M_c se determina cu relatia:

unde: - M_M - momentul maxim al motorului;

- i'_t - raportul de transmitere de la motor la angrenaj;

- k_d=1,5 - coeficientul dinamic.

Valorile efective ale efortului unitar s_ef se compara în acest caz cu efortul unitar de curgere s_c al materialului rotilor dintate.

În tabelul VII.5. sunt prezentate valorile efortului unitar efectiv de încovoiere pentru toate treptele din cutia de viteze

Tabelul 7.5. Valorile efortului unitar efectiv de încovoiere

7.4.3. Calculul de rezistenta la presiunea de contact

Sub actiunea solicitarilor de contact de pe flancurile dintilor poate aparea oboseala straturilor de suprafata (sub forma de ciupituri, sfarâmari si mai rar cojire) si deformarea plastica a flancurilor dintilor (sub forma de laminare, ciocanire, încretire, ridare).

Determinarea presiunii de contact la sarcini nominale (de regim) se face utilizând relatia lui Hertz:

unde: - y_m - coeficientul de material;

- y_fc - coeficient de forma în punctul de rostogolire;

- y_ec - gradul de acoperire asupra capacitatii flancurilor.

Deformarea permanenta a flancurilor dintilor la solicitarile de contact are loc când eforturile unitare de contact, fie datorita unor suprasarcini, fie datorita ungerii sau randamentului termic necorespunzator, depasesc limita de curgere.

Pentru calculul de rezistenta la presiunea de contact sub actiunea sarcinilor de vârf, momentul M_c se înlocuieste cu momentul dinamic M_d.

Tabelul 7.6. Valorile efortului unitar efectiv de încovoiere

7.4.4. Verificarea la durabilitate a angrenajelor

În afara unei rezistente insuficiente la sarcini nominale sau de vârf, scoaterea din functiune a angrenajelor în exploatare apare frecvent datorita depasirii limitei de rezistenta a materialului, provocata de sarcini periodice variabile. Durabilitatea angrenajelor este caracterizata de capacitatea de functionare îndelungata pâna la atingerea valorilor maxime permise ale uzurilor si pâna la aparitia oboselii materialului.

Pentru efectuarea calcului de durabilitate se considera ca motorul dezvolta un moment mediu echivalent M_ech, la o turatie medie echivalenta w_ech

Momentul mediu echivalent se calculeaza cu relatia:

unde: - M_rmed - momentul mediu la rotile motoare;

- i_cvmed - raportul de transmitere mediu al cutiei de viteze;

h_t - randamentul mecanic al transmisiei.

Pentru calculul momentului mediu la rotile motoare se utilizeaza relatia:

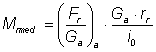
unde:- 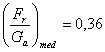forta specifica medie la rotile motoare;

- G_a - greutatea automobilului;

- r_r - raza de rulare a rotii;

- i₀ - raportul de transmitere al transmisiei principale.

Raportul de transmitere mediu al cutiei de viteze i_cvmed se determina cu relatia:

unde: - b_k - timpul relativ de utilizare a treptei de viteze;

- i_cvk - raportul de transmitere în treapta k de viteza;

Turatia medie echivalenta se calculeaza cu relatia:

unde: - - viteza medie de deplasare a automobilului.

Numarul de solicitari la care este supus un dinte, pe durata exploatarii între doua reparatii capitale (considerat ca durabilitate necesara), se determina cu relatia:

unde: - b - timpul relativ de utilizare a treptei respective;

- i"_t - raportul de transmitere de la rotile motoare pâna la angrenajul calculat;

- r_r - raza de rulare a rotii.

7.4.5. Calculul la solicitarea de oboseala la încovoiere

Determinarea efortului unitar efectiv de încovoiere la solicitarea de oboseala se determina, prin înlocuirea momentului M_c cu M_ech i'_t, M_ech fiind determinat si i'_t raportul de transmitere de la motor la angrenajul calculat.

Eforturile unitare efective obtinute la calculul la oboseala a danturii se compara cu efortul unitar la oboseala la încovoiere dupa ciclul pulsator s_N, dat de relatia:

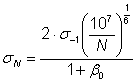
unde: - s - efortul unitar pe ciclu simetric;

s_r - efortul unitar de rupere;

- N - numarul de cicluri pentru roata dintata care se calculeaza;

Angrenajele verificate sunt considerate sunt considerate corespunzatoare din punctul de vedere al rezistentei la oboseala daca este satisfacuta inegalitatea:

unde: - k' - coeficientul de siguranta la calculul la oboseala; coeficientul k' se poate calcula cu relatia:

unde: - - coeficient de dinamicitate;

- c - coeficientul de siguranta, se determina cu relatia:

- k₁ - coeficient ce tine seama de concentratia sarcinii pe lungimea dintelui;

- k₂ - coeficient care tine seama de siguranta necesara de functionare;

- k₃ - coeficient care tine seama de precizia metodelor de calcul;

- coeficienti care tin seama de precizia de prelucrare si de calitatea

suprafetelor flancurilor dintilor

În tabelul 7.7. sunt prezentate valorile efortului unitar efectiv de încovoiere la solicitarea de oboseala la încovoiere pentru fiecare treapta din cutia de viteze.

Tabelul 7.7. Solicitarea de oboseala la încovoiere

7.4.6 Calculul la oboseala la solicitarea de contact

Efortul unitar efectiv de contact de contact, p_efc, se determina, în acest caz cu relatia (7.14), unde forta tangentiala F_t=F_{t ech}, care se ia în calcul, corespunde momentului mediu echivalent, M_ech, dezvoltat la o turatie medie echivalenta w_ech

Valorile eforturilor unitare efective de contact p_efc calculate nu trebuie sa depaseasca efortul unitar admisibil de contact p_ac pentru asigurarea durabilitatii impuse.

Efortul unitar admisibil la contact este dat de relatia:

unde:   - p_Nc - efortul unitar de contact la oboseala, pentru un anumit numar de cicluri echivalente N_ech;

- c' - coeficient de siguranta;

Efortul unitar de contact pentru calculul de oboseala se determina cu relatia:

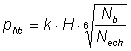
În cazul în care sunt cunoscute eforturile admisibile de contact, p_ac ale otelurilor din care sunt executate rotile dintate, pentru calculul la oboseala al flancurilor dintilor, aceste eforturi trebuie corectate cu ajutorul coeficientului durabilitatii la solicitarea de contact k_nc,dat de relatia:

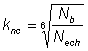
unde: - N_b - numarul ciclurilor durabilitatii de baza;

- N_ech - numarul de cicluri de solicitare corespunzatoare durabilitatii cerute.

În tabelul 7.8. sunt prezentate valorile efortului unitar efectiv de încovoiere la solicitarea de oboseala la contact pentru fiecare treapta din cutia de viteze.

Tabelul 7.8. Solicitarea de oboseala la contact

7.5. Calculul arborilor si calculul rectiunilor

Arborii sunt solicitati la torsiune si la încovoiere sub actiunea fortelor din organele sustinute (roti dintate si elemente de cuplare) si organele de sustinere (lagare).

Metodologia de calcul al arborilor cutiilor de viteze cuprinde determinarea schemei de încarcare a arborilor, calculul reactiunilor, calculul momentelor de torsiune si încovoiere, determinarea marimii sectiunilor si verificarea la rigiditate.

7.5.1. Determinarea schemei de încarcare a arborilor

si calculul reactiunilor

Încarcarile arborilor cutiilor de viteze sunt determinate de fortele din angrenarea rotilor dintate sustinute de arbori si din lagarele de montare în carterul cutiei. În figura 7.11. se prezinta schema de încarcare pentru arborii cutiei de viteze cu doi arbori, în cazul obtinerii treptei k de viteza.

Fortele din angrenare se determina tinând seama de faptul ca asupra arborilor actioneaza forte în planuri diferite, pentru usurarea calculelor, aceste forte se descompun în componente continute în planul format de arborii mecanismului reductor si în componente perpendiculare pe acest plan. Datorita faptului ca la schimbarea treptelor de viteza se modifica atât fortele, cât si pozitia rotilor active în raport cu reazemele, se schimba si reactiunile din lagare, motiv pentru care se impune determinarea lor prin cuplarea fiecareia din treptele cutiei de viteze.

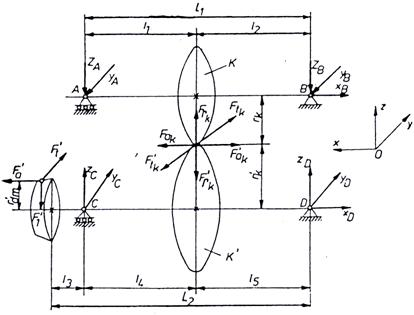
Fig.7.11. Scheme de încarcare a arborilor din cutiile de viteze

Momentul încovoietor echivalent, calculat dupa teoria a III-a de rupere (ipoteza efortului tangential maxim):

Diametrul arborelui în sectiunea calculata se determina cu relatia:

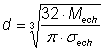
unde: - s_{a ech} - efortul unitar echivalent admisibil.

La calculul arborilor se stabilesc momentele M_i si M_t pentru fiecare treapta de viteza, luându-se în consideratie situatia cea mai dezavantajoasa.

În scopul asigurarii unei rigiditati suficiente, efortul unitar admisibil se adopta în functie de efortul corespunzator limitei de elasticitate în relatia s_e s_ai

Tabelul 7.6. Relatii pentru calculul reactiunilor din lagarele cutiilor de viteza

Tabelul 7.7. Fortele din angrenaje pentru arborele primar

Tabelul 7.8. Fortele din angrenaje pentru arborele secundar

În tabelele 7.9. si 7.10 sunt prezentate valorile momentelor si a diametrelor arborilor obtinute pentru fiecare treapta de viteza.

Tabelul 7.9. Momentele încovoietoare pentru arborele primar

Tabelul 7.10. Momentele încovoietoare pentru arborele secundar

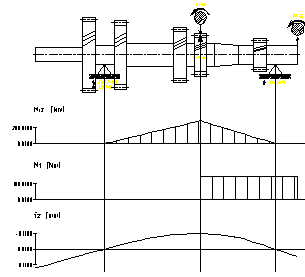
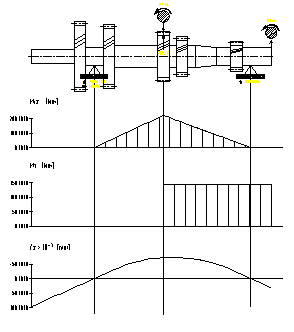
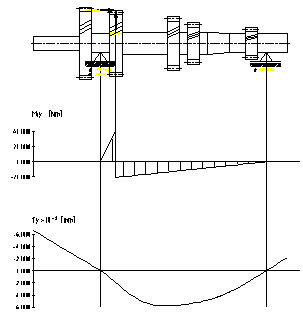
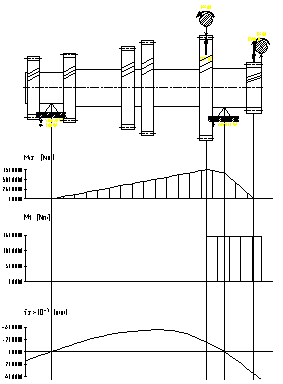
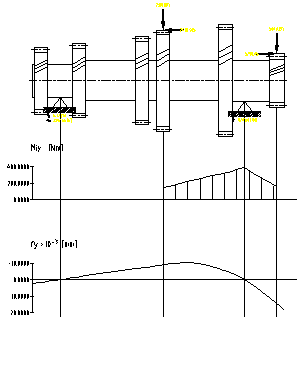
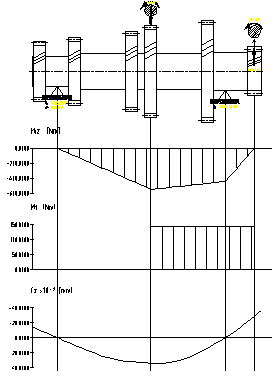
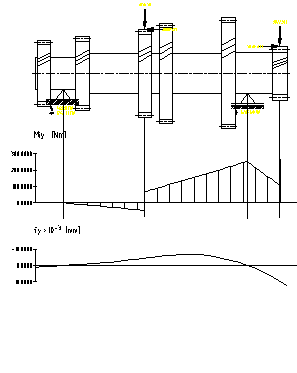
În figurile 7.12,., 7.16. sunt prezentate diagramele de momente pentru arborele primar, iar în figurile 7.17.,., 7.21. sunt prezentate diagramele de momente pentru arborele secundar al cutiei de viteze.

a) plan orizontal b) plan vertical

Fig.7.12. Diagramele de momente pentru arborele

primar corespunzator treptei întâi

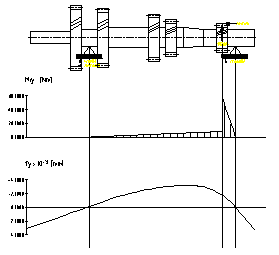
a) plan orizontal b) plan vertical

Fig.7.13. Diagramele de momente pentru arborele

primar corespunzator treptei a doua

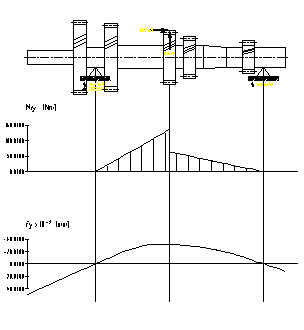
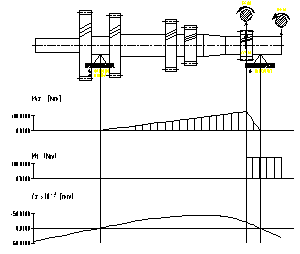
a) plan orizontal b) plan vertical

Fig.7.14. Diagramele de momente pentru arborele

primar corespunzator treptei a treia

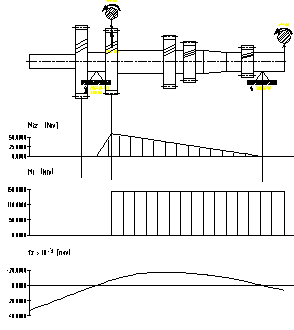
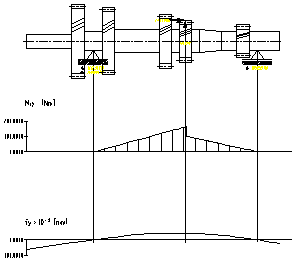
a) plan orizontal b) plan vertical

Fig.7.15. Diagramele de momente pentru arborele

primar corespunzator treptei a patra

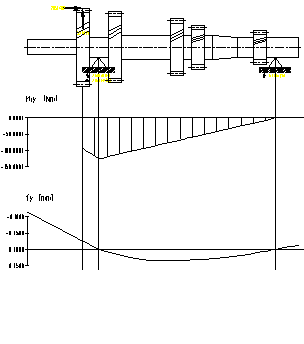
a) plan orizontal b) plan vertical

Fig.7.15. Diagramele de momente pentru arborele

primar corespunzator treptei a cincea

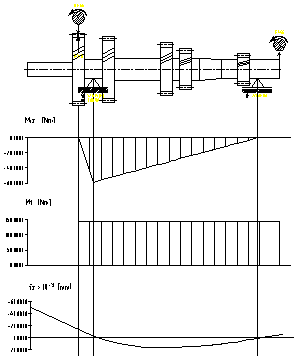
a) plan orizontal b) plan vertical

Fig.7.16. Diagramele de momente pentru arborele

secundar corespunzator pimei trepte

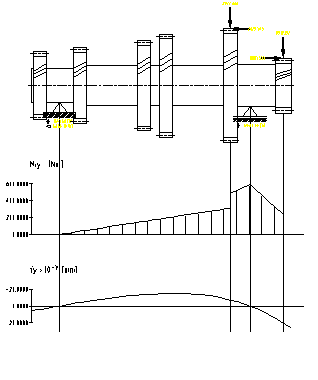
a) plan orizontal b) plan vertical

Fig.7.17. Diagramele de momente pentru arborele

secundar corespunzator treptei a doua

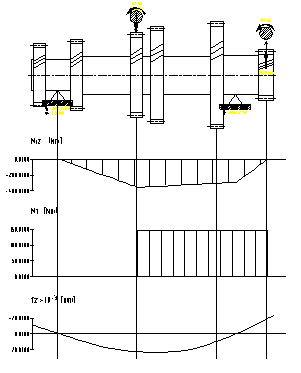
a) plan orizontal b) plan vertical

Fig.7.18. Diagramele de momente pentru arborele

secundar corespunzator treptei a treia

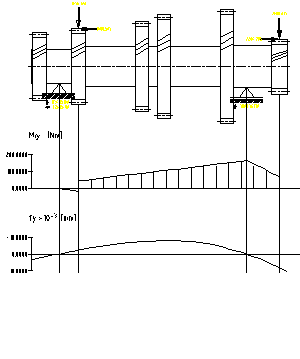
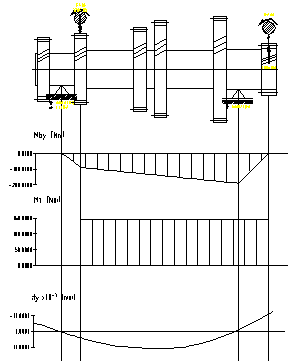
a) plan orizontal b) plan vertical

Fig.7.19. Diagramele de momente pentru arborele

secundar corespunzator treptei a patra

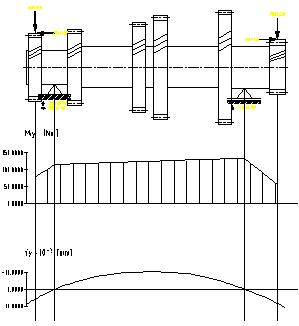
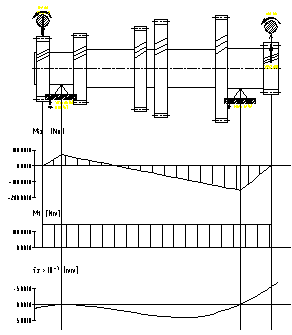
a) plan orizontal b) plan vertical

Fig.7.20. Diagramele de momente pentru arborele

secundar corespunzator treptei a cincea

Pentru arborele secundar adopt conform STAS 1769-68 caneluri cu profil dreptunghiular serie mijlocie cu urmatoarele caracteristici geometrice:

- numar de caneluri:   z=8;

- diametrul interior:   d=42 [mm];

- diametrul exterior:   D=48 [mm].

Diametrele arborilor se vor alege constructiv respectând diametrul minim calculat.

7.5.3. Verificarea rigiditatii

Solicitarile de încovoiere si de rasucire ale arborilor determina aparitia unor deformatii elastice, care conduc la suprasolicitari ale dintilor rotilor în angrenare, modifica legile angrenarii si reduc gradul de acoperire.

În cazul unor deformatii mari ale arborilor, polul angrenarii executa o miscare oscilatorie în jurul unei pozitii teoretice, determinând, pentru arborele condus, o miscare de rotatie neuniforma si o functionare zgomotoasa pentru cutia de viteze.

Din aceste considerente, dupa dimensionarea arborilor din conditia de rezistenta la solicitari compuse (torsiune si încovoiere) se face si verificarea rigiditatii (calculul deformatiilor). Pentru calculul sagetii arborilor se considera arborele de sectiune constanta, încarcat cu o singura forta. Folosind relatiile de calcul din tabelul 7.7., se pot determina sagetile în plan orizontal, f_y, si în plan vertical f_z. În cazul în care asupra arborelui actioneaza simultan mai multe forte, sageata rezultanta, în sectiunea si în planul considerat, este data de suma algebrica a sagetilor ce apar sub actiunea fortelor luate individual.

Cunoscând valoarea sagetii în plan orizontal si vertical se determina sageata rezultanta cu relatia:

unde:   - f_amax=0,13.0,15[mm] - sageata maxima admisibila pentru treptele superioare;

- f_amax=0,15.0,25[mm] - sageata maxima admisibila pentru treptele inferioare.

Tabelul 7.11. Relatii pentru calculul deformatiilor

arborilor solicitati la încovoiere

În tabelul 7.12. si 7.13. sunt prezentate valorile sagetilor calculate pentru arborele principal, respectiv pentru arborele secundar.

Sau utilizat notatiile:

- f_y   - sageata pe directia axei Oy;

- f_z   - sageata pe directia axei Oz;

- f - sageata rezultanta;

- f_ytr, f_ztr, f_tr - sagetile arborelui secundar datorate transmisiei principale.

Tabelul 7.12. Sagetile pentru arborele primar

Tabelul 7.13. Sagetile pentru arborele secundar

7.6. Calculul de alegere a lagarelor cutiei de viteze

În calculul de determinare a rulmentilor se tine seama de caracterul sarcinilor, de conditiile de montaj si de durata de functionare.

Dependenta dintre aceste marimi este data de relatia:

unde: - C - capacitatea de încarcare dinamica necesara a rulmentului;

- D - durabilitatea necesara rulmentului;

- F_e - forta echivalenta medie;

- p - exponent ce tine cont de tipul rulmentului (p=3, pentru rulmenti cu bile; p=10/3, pentru rulmenti cu role).

Durabilitatea necesara a rulmentului, egala pentru toate lagarele cutiei de viteze, se da în kilometrii parcursi. Pentru obtinerea durabilitatii în milioane de rotatii se utilizeaza relatia:

unde: - i_{cv med} - raportul de transmitere mediu al cutiei;

- D - durabilitatea necesara a rulmentului;

- i₀ - raportul de transmitere al puntii motoare;

- i - raportul de transmitere de la motor la arborele al carui lagar se calculeaza

- r_r - raza de rulare a rotii motoare.

La determinarea fortei echivalente medii F_e se tine seama de fortele axiale si radiale ce apar în lagare în fiecare treapta a cutiei de viteze. Ea se determina cu relatia:

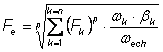
unde: - F_k - forta echivalenta corespunzatoare treptei k de viteza;

b_k - timpul relativ de utilizare a treptei k de viteza;

w_ech - viteza unghiulara echivalenta a motorului.

Forta F_k se determina cu relatia:

[N]

Rb

[N]

Rc

[N]

Rd

[N]

I

II

III

IV

V