EXEMPLE DE CALCUL DE DIMENSIONARE

EXEMPLE DE CALCUL DE DIMENSIONARE

4.1. Motor asincron cu colivie normala.

Sa se proiecteze un motor asincron trifazat capabil sa dezvolte un cuplu maxim de M_m = 100 N m (numai calculul electromagnetic), cu urmatoarele date nominale:

P_n = 4 kW;

U_n = 380 V;

f₁ = 50 Hz;

n₁ = 1000 rot/min;

m = 3;

Tipul constructiv: IM B3 STAS 3998/2-74;

Gradul de protectie: IP 23 STAS 625-85;

Constructia rotorului: rotor in scurtcircuit - colivie normala;

M_m/M_n = 2,5;

Serviciul: S₁ (continuu) STAS 1893/1-87;

Conditii de functionare: normale, conform STAS 1893/1-87.

4.1.1. Determinarea marimilor de calcul.

Numarul de perechi de poli, (conform relatiei (3.1):

.

Puterea aparenta nominala, S_n (relatia (3.2)) , si curentul nominal pe faza, I_nf (relatia (3.3).

Optam pentru conexiunea fazelor statorice in stea:

kVA;

h = 0,9 (figura 3.3);

cos j = 0,8 (figura 3.4).

A.

Tensiunea nominala pe faza, impusa prin tema de proiect, este U_nf = 220 V.

Puterea aparenta interioara (relatia 3.10.a)

S_i = k_E S_n = 0,97 5,55 = 5,38 kVA;

k_E = 0,97 (figura 3.5).

4.1.2. Calculul dimensiunilor principale.

Are drept scop stabilirea diametrului interior, D, a lungimii ideale, l_i, ale statorului precum si a latimii intrefierului.

a) Diametrul interior (orientativ), conform relatiei (3.14):

.

C = 175 J/dm³, din figura 3.8.

Din figura 3.7 se observa ca l = 0,5 ÷ 1,75. Se estimeaza λ = 1,2.

Obtinem pasul polar:

b) Lungimea ideala, l_i (conform relatiei 3.18):

;

unde:

factorul de forma, k_B = 1,08 (pentru k_sd = 1,2);

coeficientul de acoperire ideala a pasului polar, a_i; pentru solicitari magnetice normale (k_sd = 1,2), a_i

factorul de infasurare, k_w = 0,91 ÷ 0,93;

inductia maxima in intrefier: B_d = 0,74 T (functie de t si p - se verifica ulterior);

patura de curent: A = 320 10² A/m; s-a adoptat in functie de pasul polar t si de numarul perechilor de poli, p, din figura 3.9.

Verificarea factorului de forma al masinii:

.

Valoarea se incadreaza in limitele recomandate pentru p = 3.

c) Determinarea latimii intrefierului.

Se determina pe baza unor relatii empirice, in functie de diametrul D si de numarul de poli 2p.

In acest caz propunem d = 0,5 mm.

Se urmareste realizarea unui intrefier cat mai mic pentru obtinerea unui factor de putere cat mai bun.

d) Geometria miezului feromagnetic.

Valorile obtinute pentru diametru si lungimea ideala permit utilizarea in prima faza a unui miez compact (vezi paragraful 3.4.)

Lungimea geometrica l_g a miezului va fi:

l_g = l_fe l_i.   

4.1.3. Infasurarea si crestaturile statorului.

Numarul de crestaturi ale statorului, Z₁(relatia (3.23)):

Z₁ = 2m₁·p·q₁;

Pentru 2p = 6 se recomanda q₁ = 3 ÷ 4; se vor efectua calculele pentru doua variante posibile, Z₁^' si Z₁^'' (Tabelul 3.1):

Z₁^' = 2 3 = 54 crestaturi;

Z₁^''= 2 4 = 72 crestaturi.

Pasul dentar, t₁:

;.

Verificand limitele recomadate pentru pasul dentar alegem varianta cu Z₁ = 72 crestaturi, deci q₁ = 4 si t₁ = 0,61 cm.

Elementele infasurarii statorului.

1) Numarul de spire pe faza (conform relatiei 3.26):

numar intreg.

Fluxul magnetic F se determina cu relatia:

F a_i t l_i B_d

F 10^-3 Wb;

spire/faza.

2)Numarul de conductoare efective dintr-o crestatura (3.27):

.

Tinand cont de conditia echilibrarii cailor de curent in paralel, pe faza, numar intreg, am ales a₁ = 3 cai de curent, in paralel.

Conditia ca numarul de bobine pe faza si pe calea de curent sa fie acelasi, la infasurarea in doua straturi, impune numar intreg:

.

Pentru a obtine tensiuni electromotoare induse, pe faza, egale si defazate cu 2p/m₁, trebuie ca numar intreg; t este cel mai mare divizor comun al lui p si Z₁.

3)Verificari necesare

A) Determinarea definitiva a numarului real de spire pe faza, conform relatiei (3.28):

.

B) Verificarea paturii de curent (relatia 3.29):

Valoarea paturii de curent obtinuta trebuie sa fie apropiata de cea adoptata initial, si se incadreaza in limitele (orientative) indicate de relatia (3.30).

C) Verificarea valorii maxime a inductiei magnetice in intrefier conform relatiei (3.31):

[T];

in care fluxul magetic util, maxim, F, se calculeaza cu relatia (3.31. a):

[Wb];

unde, w₁ = 280 spire, este valoarea definitiva a numarului de spire; k_w1 va avea valoarea corespunzatoare tipului de infasurare ales.

Intrucat am optat pentru o infasurare in doua straturi, cu pas scurtat, y₁= 10 (pasul diametral, in crestaturi, fiind cres-taturi), la q = 4 si un raport b_y = y₁/y_t = 0,833, obtinem un factor de infasurare de 0,926 (vezi Anexa 1 Tabelul 1-1).

Rezulta:

;

.

Valoarea obtinuta pentru inductie se incadreaza in limitele orientative indicate pentru abaterile inductiei.

Tipul infasurarii si dimensiunile crestaturii

1) Sectiunea efectiva si dimensiunile conductorului (conform relatiei (3.33):

.

Densitatea de curent J₁ se alege in functie de clasa de izolatie a infasurarii, de tensiunea nominala si de eficacitatea si tipul ventilatiei. Pentru clasa de izolatie F si U<1000V, se recomanda J₁ = 5,5 ÷7,5 A/mm². Alegand J₁ = 6,5 A/mm², se obtine:

Rezultatul obtinut permite utilizarea unei infasurari cu conductor rotund. ( vezi tabelul 3.2.) Forma crestaturii poate fi in acest caz ovala sau trapezoidala (fig. 3.12).

Diametrul efectiv al conductorului se alege conform STAS-685-75 (anexa 4 tabelul 4-1): d = 0,75 mm, la o sectiune s_Cu1 = 0,4418 mm².

Diametrul conductorului izolat (izolatie cu email tereftalic): d_iz = d + d^' = 0,75 + 0,05 = 0,8 mm, conform anexei 6.

2) Dimensiunile crestaturii.

In continuare sunt prezentate etapele de calcul necesare dimensionarii crestaturii.

a) Latimea constanta a dintelui, b_d1, (relatia (3.35):

[m].

unde,

B_d1,adm = 1,4÷1,7 T (vezi paragraful 3.5.2)

Alegem B_d1,adm = 1,4 T, iar l_i l_Fe:

b) Se determina sectiunea neta a crestaturii, - fara pana si istm, fara izolatia crestaturii dar, cu izolatia dintre straturi (relatia (3.36):

[mm²];

mm².

c) Se face constructia la scara, respectand valoarea latimii b_d1 si variind inaltimea crestaturii, pana cand se ajunge cu valoarea masurata, pe desen, a lui , la valoarea rezultata din calcul (vezi figura 4.1). Am optat pentru o crestatura trapezoidala.

Unghiul dintre axele de simetrie a doua crestaturi vecine (doi dinti vecini) este (relatia (3.37)):

.

d) Se calculeaza deschiderea crestaturii, a_s (3.38):

a_s ³ d_iz + 1,5 [mm].

Conductorul trebuie sa poata fi introdus in crestatura in timp ce este protejat de izolatia de crestatura.

a_s ³ 0,8 + 1,5 = 2,3 mm => a_s = 2,3 mm.

e) Tinand cont de grosimea izolatiei de crestatura, de grosimea izolatiei dintre straturi si grosimea penei, se definitiveaza forma crestaturii, deci, implicit, inaltimea acesteia si a dintelui.

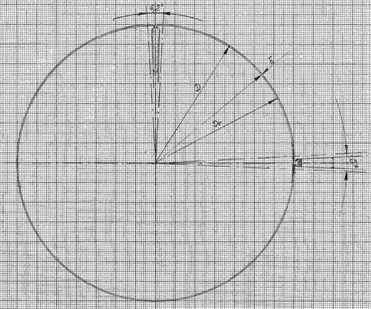
Figura 4.1. Constructia la scara a crestaturii statorice,

respectiv rotorice.

In urma definitivarii formei si marimii crestaturii, rezulta urmatoarele dimensiuni ale acesteia: a_s = 2,3 mm; h₀ = 1 mm; h₁ = 15 mm; h₂ = 2,5 mm; h₃ = 1,5 mm; b = 4,5 mm.

Inaltimea crestaturii va fi h_c1 = 20 mm si va fi egala cu inaltimea dintelui, h_d1.

Verificari necesare

Valoarea exacta a densitatii de curent (relatia (3.44)):

A/mm².

Valoarea se incadreaza in limitele indicate (paragraful 3.5.1).

Inductia magnetica in jugul statoric si dimensionarea acestuia

Inaltimea jugului statoric se calculeaza cu relatia (3.45):

[m];

unde, B_j1 este inductia in jugul statoric, aleasa intre limitele 1,35 ÷ 1,55 T (conform paragrafului 3.5.2).

Pentru B_j1 =1,4 T, obtinem:

Diametrul statoric exterior, D_ext:

D_ext = D + 2 (h_c1 + h^'_j1) = 140 + 2 (20 + 15) = 210 mm.

4.1.4. Infasurarea si crestaturile rotorului.

Numerele de crestaturi favorabile pentru rotor, pentru 2p = 6 si Z₁ = 72, sunt: 56, 58, 62, 82, 84, 86, 88 (crestaturi drepte), valori in conformitate cu tabelul (3.4).

In continuare se va efectua calculul pentru doua variante de rotor: Z₂ = 58 crestaturi si Z^*₂ = 88 crestaturi. Toate marimile calculate pentru cea de-a doua varianta vor fi notate cu "*".

Este propusa o colivie simpla, cu bare de forma ovala, de aluminiu (figura 3.19, c).

Pasul dentar al rotorului (relatia (3.52):

[cm];

in care, D_r = D - 2d [cm], este diametrul exterior al rotorului (3.53):

D_r = 14 - 2·0,05 = 13,9 cm.

Obtinem:

si .

4.1.5. Parametrii infasurarii statorice.

1)Determinarea reactantei infasurarii statorice (relatia 3.63).

[W]; sau,

[W

a) Permeanta specifica a scaparilor in crestatura.

Se determina in functie de forma crestaturii si tipul infasurarii. Pentru crestatura trapezoidala considerata, avem urmatoarea relatie de calcul (vezi paragraful 3.9.3.):

Coeficientii si se determina in functie de pasul relativ al infasurarii, In acest caz, b_y = 0,833 (vezi anexa 1, tabelul 1-1), deci se vor utiliza relatiile:

;

;

cu: a_s = 2,3 mm; h₀ = 1 mm; b = 4,5 mm; h₁ = 15 mm; h₂ = 2,5 mm; h₃ = 1,5 mm.

b) Permeanta geometrica specifica a scaparilor diferentiale.

Prin scapari diferentiale se intelege diferenta dintre campul magnetic real (rezultant) din intrefier si campul magnetic al undei sale fundamentale.

Determinarea marimilor necesare calcularii lui l_d1

Coeficientul de amortizare. Pentru masinile cu rotorul in scurtcircuit, r_d1 se alege in functie de q₁ si Z₂/p (vezi tabelul 3.8). In acest caz:

q₁ = 4; 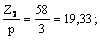obtinem r_d1 r _d1

Coeficientul k₀₁.

Factorul Carter.

In aceasta etapa de calcul s-a considerat ca:

.

.

Coeficientul de scapari diferentiale.

Pentru scurtarea propusa a pasului diametral (y/y_t = 5/6) si q = 4, se obtine s_d1 = 0,006 (vezi tabelul 3.9).

Permeanta geometrica specifica, a scaparilor diferentiale, va fi:

;

.

c) Permeanta geometrica specifica a scaparilor in partile frontale.

Pentru infasurarea propusa pentru stator, in doua straturi, relatia de calcul este (vezi relatia (3.77)):

in care, l_f1 este lungimea medie a partii frontale a bobinei, in [cm] si se poate aproxima, in acest stadiu, cu ajutorul relatiei:

S-a considerat ca infasurarea statorica este alcatuita din bobine avand capetele rotunde. Pentru 2p = 6, avem A = 0 (vezi paragraful 3.9.1.B).

d) Permeanta geometrica specifica totala, a infasurarii statorului:

Deci, reactanta de scapari pe faza, a infasurarii statorului, va fi:

2) Rezistenta pe faza a infasurarii statorice (relatia (3.62)).

;

l_w1,med = l_g + l_f1 = 0,096 + 0,0958 = 0,19 m,

Pentru clasa de izolatie F, q C, iar r_20,Cu W·mm²/m.

r_115,Cu r_20,Cu W·mm²/m;

k_r 1. la f₁ = 50 Hz.

Relatii calculate in conformitate cu indicatiile din paragraful 3.9.2.

4.1.6. Dimensionarea coliviei rotorice.

Calculul de dimensionare se face pornind de la faptul ca valoarea cu-plului maxim al motorului este impusa prin tema de proiectare (M_m = 100 N·m), pe baza relatiilor cuplului maxim si alunecarii critice.

Din relatia (3.79) a cuplului maxim,

,

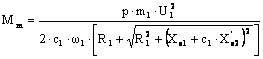se determina reactanta de scapari, raportata, a infasurarii rotorice,;

La masinile asincrone normale, c₁ = 1,04

Reactanta de scapari rotorica, pe faza, va fi (relatia (3.80)):

In cazul rotorului in scurtcircuit: m₂ = Z₂; w₂ = 1/2; k_w2 = 1.

;

Din relatia (3.81) a alunecarii critice (corespunzatoare cuplului maxim),

,

impunand o valoare lui s_m, il determinam pe , rezistenta rotorica rapor-tata (relatia (3.82.a):

[W

Impunem s_m = 0,2:

Rezistenta rotorica pe faza:

Avand valorile rezistentei si reactantei de scapari rotorice, se incearca dimensionarea crestaturii rotorului.

Cu ajutorul valorii rezistentei rotorice, se determina rezistenta unei bare, R_b si sectiunea acesteia. Intr-o prima aproximatie, se poate considera ca, R_b (0,7 ÷ 0,8)·R₂.

,

unde,

r_20,Al W·mm²/m:

r_115,Al r_20,Al W·mm²/m;

Se verifica incadrarea densitatii de curent in limitele admise.

Curentul prin bara (vezi relatia (3.91):

[A];

k_I = 0,85 ( se estimeaza in functie de valoarea lui cos j

Densitatea de curent (vezi relatia (3.92):

J_b = 2,33 [A/mm²];

Intrucat valorile obtinute nu se incadreaza in limitele recomandate, J_b = 3 ÷ 5,5 A/mm² pentru bare din aluminiu, se vor alege, in continuare, sectiuni sensibil mai mici.

Impunem J_b = 3 A/mm² si vom obtine s_b = 63 mm², respectiv .

Latimea dintelui rotoric (relatia (3.94):

pentru o inductie, in dintele rotoric, de 1,6 T, obtinem:

Intrucat valoarea b^*_d2 e necorespunzatoare din motive tehnologice, in continuare, vom renunta la varianta de rotor cu 88 de crestaturi.

Alegem o colivie normala, turnata, crestaturile rotorice fiind de forma ovala (dinti cu pereti paraleli) - vezi figura 3.32.e. Dimensiunile crestaturii rotorice se obtin dupa constructia la scara a acesteia (vezi figura 4.1):

b₀ = 1 mm; h₀ = 0,5 mm; b₁ = 3,2 mm; b₂ = 2 mm; h₁ = 19,8 mm.

Definitivarea crestaturii rotorice se face tinand cont de valoarea calculata a lui X_s

Permeanta geometrica specifica totala, a rotorului, este:

a) Permeanta geometrica specifica a scaparilor in partile frontale, l_f2 (vezi relatia (3.95):

in care:

D_i - diametrul mediu al inelului de scurtcircuitare, in [cm];

a, b - lungimea, respectiv latimea sectiunii inelului, in [cm]; aceste dimensiuni se pot estima in aceasta faza, din sectiunea inelului (figura 3.33 a).

Se calculeaza curentul prin inelul coliviei (vezi (3.85)):

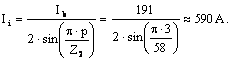
Impunand densitatea de curent in inel, J_i = 2,4 A/mm², J_i J_b, obtinem sectiunea inelului:

Inaltimea totala a barei impune limita minima pentru a:

a ³ 25 mm;

Alegem a = 25 mm.

Colivia fiind turnata, deducem imediat si latimea inelului:

Pe baza rezultatelor obtinute se poate determina diametrul mediu al inelului, D_i: D_i = D_r - a = 13,9 - 2,5 = 11,4 cm.

Rezulta:

b) Permeanta geometrica specifica a scaparilor diferentiale, l_d2(vezi relatia (3.96):

Cu dimensiunile aproximative ale crestaturii rotorice, identice cu cele ale sectiunii barei (colivie turnata), se recalculeaza k_C2 si, implicit, k_C:

Pentru rotorul in scurtcircuit propus, in functie de Z₂ si p, gasim s_d2 = 0,008 (vezi Tabelul 3.10).

Se obtine:

c) Permeanta geometrica specifica a scaparilor in crestatura, l_c2

Se incearca determinarea lui h₀ si b₀, pentru crestatura aleasa in rotor, astfel incat sa se obtina o permeanta specifica de scapari in crestatura cat mai apropiata de valoarea necesara (figura 3.32, e).

Alegem h₀ = 0,8 mm si b₀ = 1 mm:

Valoarea corespunde celei impuse de necesitatea obtinerii cuplului maxim cerut, iar corectiile facute asupra lui h₀ si b₀ nu influenteaza dimen-siunile precalculate ale crestaturii si dintelui.

Dimensionarea jugului rotoric.

Dimensionarea jugului rotoric se face pornind de la idea mentinerii inductiei magnetice in limitele admise: .

Inaltimea precalculata a jugului, , rezulta din relatia (3.103):

[m];

Diametrul interior al rotorului, D_ir

;

h_c2 = h_d2 = 23,5 mm (din constructia la scara a crestaturii).

Inaltimea finala a jugului rotoric:

Verificarea inductiei magnetice, in jug:

4.1.7. Tensiunea magnetomotoare pe o pereche de poli.

Tensiunea magnetomotoare, pe o pereche de poli, se determina ca suma a tensiunilor magnetice ale celor cinci portiuni distincte ale circuitului magnetic al masinii: intrefier, dinte statoric, dinte rotoric, jug statoric si jug rotoric.

a) Tensiunea magnetica a intrefierului, pentru o pereche de poli (3.105):

[A],

k_C = k_C1·k_C2 .

Coeficientul Carter se calculeaza mai exact:

unde:

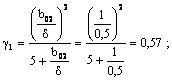
k_C = k_C1·k_C2 = 1,05·1,17 = 1,23.

b) Tensiunea magnetica a dintilor statorici, pentru o pereche de poli (vezi relatia (3.107):

[A].

Intrucat b_d1 este constanta, H_d1 se ia din curba de magnetizare a materialului feromagnetic al miezului, in functie de valoarea inductiei magnetice in dinte, B_d1 si calitatea tolei utilizate (vezi anexa 2).

B_d1 = 1,4 T Þ H_d1 = 10 A/cm;

U_md1 = 2 10 = 40 A.

c) Tensiunea magnetica a dintilor rotorici, pentru o pereche de poli (relatia 3.111):

[A];

H_d2 - se ia din curba de magnetizare a tablei folosite la rotor (anexa 2), pentru inductia magnetica in dinte, calculata cu relatia:

Verificarea coeficientului partial de saturatie magnetica.

Valoarea este apropiata de cea estimata initial, k_sd = 1,2.

d) Tensiunea magnetica a jugului statoric pentru o pereche de poli (relatia (3.114):

U_mj1 = z ·L_j1·H_j1 [A] .

[cm], lungimea medie a liniei de camp magnetic, in jugul statoric:

B_j1 = 1,4 T Þ H_j1 = 10 A/cm

z = 0,4 (se alege din anexa in functie de valoarea lui B_j1).

e) Tensiunea magnetica a jugului rotoric, pentru o pereche de poli (relatia (3.115):

U_mj2 = z ·L_j2·H_j2 [A] .

B_j2 = 1,39 T; Þx = 0,41 (conform figurii 3.32)

si H_j2 = 9,5 A/cm (din anexa 2).

U_mj2 = 0,41·1,28·9,5 5 A .

f) Tensiunea magnetomotoare a circuitului magnetic, pe o pereche de poli (relatia (3.116):

U_mcirc = U_md + U_md1 + U_md2 + U_mj1 + U_mj2 [A].

U_mcirc = 716 + 40 + 70,5 + 13 + 5 = 845 A.

g) Coeficientul total de saturatie magnetica(relatia (3.117).

4.1.8. Curentul de magnetizare.

Curentul de magnetizare, se determina cu relatia (3.118):

In procente:

4.1.9. Recalcularea parametrilor motorului asincron.

Calculul electromagnetic al motorului fiind complet, cu rezultate satisfacatoare sub aspectul solicitarilor electrice si magnetice, se recalcu-leaza parametrii masinii, tinand cont de dimensiunile rezultate din calcul. In cazul relatiilor de calcul deja utilizate, se vor efectua direct inlocuirile numerice.

A. Stator.

1. Rezistenta statorica, pe faza, R₁.

Valoarea acesteia a fost calculata exact, deci R₁ = 1,976 W

2. Reactanta de scapari statorica, X_s

a) Permeanta specifica a scaparilor in crestatura: l_c1 = 2,24, nemodi-ficata.

b) Permeanta specifica a scaparilor diferentiale:

c) Permeanta geometrica specifica a scaparilor in partile frontale: l_f1 = 0,803, nemodificata.

Rezulta:

3. Reactanta utila sau de magnetizare.

B. Rotor.

1. Rezistenta rotorica, pe faza.

.

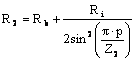Rezistenta barei:

Rezistenta inelului, corespunzatoare unei faze:

in care, L_i este lungimea portiunii de inel, in [m]:

.

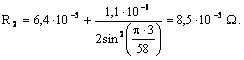
Rezistenta rotorica, raportata la stator:

2. Reactanta de scapari a rotorului, pe faza.

a) Permeanta specifica a scaparilor in crestatura: l_c2 = 3,24, nemodi-ficata.

b) Permeanta specifica a scaparilor diferentiale:

c) Permeanta geometrica specifica a scaparilor in partile frontale: l_f2 = 0,49, nemodificata.

Rezulta:

Reactanta de scapari rotorica, raportata la stator:

4.1.10. Calculul caracteristicilor motorului.

Caracteristicile care intereseaza in acest caz, sunt:

cuplul maxim, M_m si alunecarea critica, s_m;

alunecarea nominala, s_n si cuplul nominal, M_n;

1. Cuplul maxim.

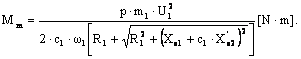
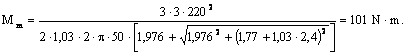
2. Alunecarea critica.

3. Alunecarea nominala.

in care,

este curentul nominal rotoric, raportat la stator

4. Cuplul nominal.