Student: Vlad Stefan - Ionut
Facultatea: Inginerie Mecanica
Sectia: Mecatronica
Grupa: 541 E
Tema proiectului
Sa se proiecteze un sistem de actionare cu motor electric pas cu pas pentru mecanismul prezentat in figura 1
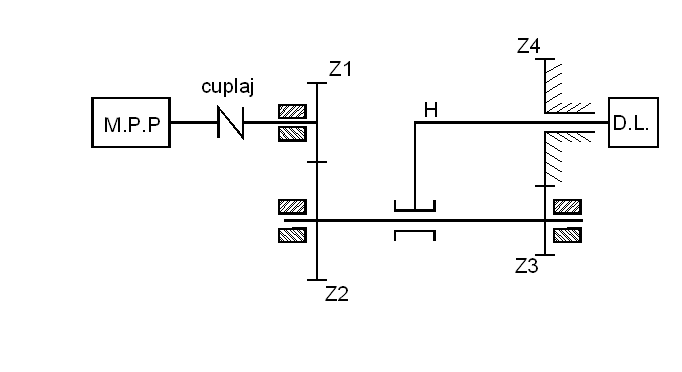
Fig.1
Unde
MPP - motor pas cu pas
z1 z2 z3 z4 - roti dintate ce alcatuiesc un mecanism planetar
Unghi de pas : 1.8°
Precizia unghiulara de pas[%] : 5
Curent nominal pe faza[A] : 1.3
Rezistenta pe faza[V
Inductanta pe faza[mH] : 16
Cuplu de regim [N*cm] : 120
Cuplu de pornire[N*cm] : 10
Inerenta rotorului[gr*cm2] : 640
masa [Kg] : 1.35
clasa de izolare : B
2. Caracteristicile motorului pas cu pas (MPP) HY200-3424 0170BX08 sunt :
Unghi de pas : 1.8°
Precizia unghiulara de pas[%] : 5
Curent nominal pe faza[A] : 1.7
Rezistenta pe faza[V
Inductanta pe faza[mH] : 5
Cuplu de regim [N*cm] : 120
Cuplu de pornire[N*cm] : 10
Inertia rotorului[gr*cm2] : 640
masa [Kg] : 1.35
clasa de izolare : B
3. Caracteristicile motorului pas cu pas (MPP) HY200-3424 0310AX08 sunt :
Unghi de pas : 1.8°
Precizia unghiulara de pas[%] : 5
Curent nominal pe faza[A] : 3.10
Rezistenta pe faza[V
Inductanta pe faza[mH] : 3.2
Cuplu de regim [N*cm] : 120
Cuplu de pornire[N*cm] : 10
Inertia rotorului[gr*cm2] : 640
masa [Kg] : 1.35
clasa de izolare : B
4. Caracteristicile motorului pas cu pas (MPP) HY200-3424 0470AX08 sunt :
Unghi de pas : 1.8°
Precizia unghiulara de pas[%] : 5
Curent nominal pe faza[A] : 4.7
Rezistenta pe faza[V
Inductanta pe faza[mH] : 1.5
Cuplu de regim [N*cm] : 120
Cuplu de pornire[N*cm] : 10
Inertia rotorului[gr*cm2] : 640
masa [Kg] : 1.35
clasa de izolare : B
Mecanismul actionat este caracterizat de urmatoarele marimi :
Nr.crt |
z |
g[mm] |
m[mm] |
Mrez[N*m] |
JDL[Kg*m2] |
f[pas/s] |
Model |
t[s] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
|
Proiectarea se va face tinand seama de posibilitatea de a utiliza 4 motoare produse de firma MDP (Franta)
Introducere. Motoare pas cu pas - caracteristici generale
Determinarea momentului de inertie redus la arborele motorului. Determinarea momentului rezistent redus la arborele motorului
Modelarea matematica a functionarii sistemului in regim dinamic
Simularea functionarii sistemului de actionare pentru comanda in tensiune: treapta, rampa, sinusoidala
Studiul stabilitatii sistemului de actionare
Comanda motorului electric pas cu p 22422p1524w as utilizand placa de achizitie de date
1. Introducere. Motoare pas cu pas - caracteristici generale
In multe dintre aplicatiile tehnice se astazi se prefera utilizarea unor sisteme de actionare electrice care utilizeaza motoare pas cu pas.
Motorul pas cu pas (denumit uneori si motor sincron cu impulsuri), transforma impulsurile electrice de tensiune in deplasari unghiulare discrete. La primirea unui impuls rotorul motorului isi schimba pozitia cu unghi bine precizat, functie de impuls. Unghiul minim de deplasare al rotorului este denumit pas. Motoarele pas cu pas permit realizarea unor sisteme auotmate de tip discret care nu au nevoie de legaturi inverse, deoarece stabilesc o corespondenta directa riguros univoca intre informatia primita si deplesarea unghiulara realizata.
Generalitati (constructie si functionare, clasificare, definitii)
Avantajele utilizarii MPP sunt urmatoarele.
- asigura univocitatea conversiei impuls-deplasare si pot fi utilizate în circuit deschis;
sunt compatibile cu tehnica numerica.
Dezavantajele utilizarii MPP sunt:
- unghi de pas, deci increment de rotatie, de valoare fixa pentru un motor
- randament scazut;
- capacitate limitata în ceea ce priveste actionarea unor sarcini cu inertie
- viteza de rotatie relativ scazuta;
- necesita o schema de comanda adaptata la tipul constructiv respectiv si relativ
complexa, pentru asigurarea unei functionari la viteze mari.
Dezvoltarea relativ recenta a MPP, precum si interesul manifestat fata de aceste motoare au determinat dezvoltarea unei game largi de tipuri de MPP.
1 Clasificarea constructiva a motoarelor pas cu pas
Din punct de vedere constructiv, MPP poate fi de tipul: solenoidal, cu reluctanta variabila, cu magnet permanent în stator, cu magnet permanent in rotor, cu magnet permanent si reluctanta variabila (hibrid), electromecanic sau, pentru cupluri mai mari, electro-hidraulic. Acesta reprezinta o combinatie între un MPP si un amplificator hidraulic.
Consta într-un electromagnet care pune în miscare o armatura mobila, ce este legata cinematic cu un cuplaj de sens unic. Cuplajul de sens unic poate fi cu bile sau cu mecanism cu clichet.
Când se alimenteaza înfasurarea electromagnetului, clichetul este atras pe un dinte al arborelui de iesire, iar atunci când înfasurarea electromagnetului nu mai este alimentata, un arc de revenire roteste arborele cu un pas. Un al doilea clichet împiedica rotirea arborelui în directia opusa. Înfasurarea electromagnetului poate fi alimentata fie în curent continuu, fie în curent alternativ.
Avantajele acestui motor sunt :
dezvolta un cuplu relativ mare;
la efectuarea pasului nu apar oscilatii;
nu necesita alimentarea înfasurarilor pentru crearea cuplului de mentinere.
Dezavantaje:
|
Fig. 3 |
1.2 MPP cu reluctanta variabila
magnetic sa prezinte reluctanta magnetica minima, adica dintii statorici si cei rotorici sa fie aliniati radial. Comutând alimentarea pe faza urmatoare se realizeaza o rotatie a rotorului, si o deplasare a dintilor rotorici fata de cei statorici, astfel încât nu vor mai fi aliniati. Apare astfel un cuplu electromagnetic reactiv, care mareste unghiul de decalaj între pozitia dintilor statorici si rotorici. Prin cresterea cuplului electromagnetic se atinge un maxim, dupa care cuplul scade din nou la zero. Aceasta reprezinta pozitia instabila, când dintii rotorici sunt aliniati între cei statorici (fig.2).
Statorul si rotorul MPP polistatorice au acelasi numar de dinti. Toate pachetele statorice sunt fixate mecanic în aceeasi carcasa, dar sunt independente din punct de vedere electric si magnetic. Pachetele rotorice sunt de asemenea fixate mecanic pe acelasi arbore, dar sunt separate din punct de vedere magnetic.
|
Fig. 2 |
- constructie mecanica simpla;
- poate fi realizat pentru o gama larga de unghiuri de pas;
- este bidirectional, deci are un numar de faze mai mare sau egal cu trei;
Dezavantajele MPP cu reluctanta variabila sunt:
- nu memoreaza pozitia si nu dezvolta cuplu electromagnetic în lipsa curentului
de comanda din fazele statorice;
- în cazul alimentarii în secventa simpla (o singura faza alimentata la un moment
dat) si în lipsa unui cuplu de frecare, rotorul efectueaza unghiul de pas cu oscilatii importante.
MPP cu reluctanta variabila se realizeaza cu trei si patru faze, mai rar cu cinci faze. MPP cu patru faze, spre deosebire de cele cu trei faze, sunt mai rapide, prezinta oscilatii mai reduse la efectuarea pasilor, au o stabilitate mai buna în regim dinamic si dezvolta un cuplu mai mare la alimentarea în secventa dubla.
MPP se pot executa cu rezistente mici sau cu rezistente mari ale înfasurarilor fazelor, fiecare caz în parte având anumite avantaje si dezavantaje, în functie de cazul concret de utilizare.
MPP cu rezistenta pe faza marita prezinta urmatoarele avantaje:
- dispozitivul electronic de comanda este mai simplu si deci mai ieftin;
- constanta de timp a fazelor, egala cu raportul L/R, este mai mica, ceea ce
permite o functionare la frecvente de comanda mai mari;
- greutatea motorului este mai mica.
Dezavantajele sunt:
MPP cu rezistenta mica a înfasurarilor fazelor au urmatoarele avantaje:
- cuplul dezvoltat este constant, indiferent de temperatura, daca sunt alimentate
la curent constant pe faze;
- disiparea de caldura pe fazele motorului este mica;
- sistemul de comanda are randament mai bun, daca se foloseste alimentarea cu
curent constant pe faza;
- în cazul alimentarii cu fortarea curentului prin tensiune, se obtin cupluri si viteze
mai mari.
Dezavantaje:
- viteza de functionare este limitata, în cazul alimentarii cu curent nominal;
- în cazul fortarii curentului, este necesar un sistem de protectie la supracurent.
|
fig.4 |
Aceste motoare se obtin
prin înlocuirea înfasurarilor de excitatie cu magneti
permanenti. In figura 4 este prezentata o sectiune printr-un
astfel de motor. Fluxul de excitatie constant al magnetilor
permanenti depinde de pozitia rotorului datorita decalajului cu +![]() a permeantei magnetice corespunzatoare la doi
poli vecini, care formeaza o faza. Decalajul zonelor dintate a
doi poli separati de magnet este +
a permeantei magnetice corespunzatoare la doi
poli vecini, care formeaza o faza. Decalajul zonelor dintate a
doi poli separati de magnet este +![]() /2. Caracteristic, pentru MPP cu magneti permanenti
si înfasurari de comanda montate pe stator este faptul ca zonele dintate sunt
saturate de fluxul total, ceea ce duce la micsorarea coeficientului de
utilizare a magnetilor.
/2. Caracteristic, pentru MPP cu magneti permanenti
si înfasurari de comanda montate pe stator este faptul ca zonele dintate sunt
saturate de fluxul total, ceea ce duce la micsorarea coeficientului de
utilizare a magnetilor.
Avantajul acestui motor consta în faptul ca memoreaza pozitia fara ca fazele sa fie alimentate. Dezavantajul principal consta în aceea ca este unidirectional, frecventa limita de comanda este scazuta, iar o modificare a proprietatilor magnetului permanent îi afecteaza performantele.
O varlanta inversa a tipului de motor prezentat anterior este cea din figura 5.
|
Fig. 5 |
Aceste motoare au în rotor un magnet permanent care magnetizeaza rotorul radial. Fazele pot fi dispuse pe rotor, ca in figura 5 sau pe stator.
Când se alimenteaza fazele de comanda, se creeaza un flux ce interactioneaza cu fluxul magnetului permanent, ceea ce face ca rotorul sa ocupe o pozitie ce corespunde reluctantei minime a circuitului magnetic.
Avantajele acestui motor sunt:
Dezavantajele principale ale acestui motor sunt:
Între cele doua rotoare este plasat un magnet permanent cilindric magnetizat axial.
Se poate construi si un MPP inversat, în care magnetul permanent cilindric sa fie plasat intre pachetele statorice.
Acest motor prezinta urmatoarele avantaje:
- în absenta alimentarii fazelor prezinta un cuplu de mentinere a rotorului;
- are un randament bun, datorita energiei înmagazinate în magnetul permanent
din stator sau rotor;
- poate functiona cu o frecventa mare de comanda.
Ca dezavantaje, se pot aminti:
-inertia mare a rotorului;
-performantele motorului sunt afectate de schimbarea caracteristicilor magnetului permanent.
Exista MPP cunoscute sub numele de MPP electromecanic si MPP electrohidraulic . Primul are constructie unitara, compacta, ce consta dintr-un circuit electromagnetic si un sistem de transmisie armonica, ce mareste cuplul de iesire si reduce pasul motorului la valori foarte mici.
Avantajele MPP din aceasta categorie sunt:
Dezavantaje:
viteza de rotatie mica;
uzura mecanica a angrenajelor
Posibilitatile motoarelor electrice pas cu pas de a dezvolta cupluri de valori mari la frecvente de comanda ridicate sunt limitate. Pentru marirea fortelor magnetice tangentiale din întrefierul motorului, si deci a cuplului dezvoltat de motor, este necesara marirea diametrului rotorului, ceea ce duce la cresterea momentului de inertie si deci la micsorarea turatiei limita de functionare pentru un cuplu de sarcina dat. Marirea cuplului util intr-un sistem de actionare cu motor pas cu pas, fara a limita turatia maxima de functionare prin marirea momentului de inertie, este posibila prin utilizarea unui motor electric pas cu pas de mica putere, in combinatie cu un amplificator de cuplu hidraulic cu piston axial, acesta din urma având un randament ridicat si un moment de inertie redus. Întregul ansamblu motor-amplificator hidraulic a primit denumirea de motor pas cu pas electrohidraulic.
Din punct de vedere al transformarilor electromagnetice specifice MPP, se poate face o clasificare într-un numar mai restrâns de grupe functionale. Aceasta noua clasificare se bazeaza pe modul de conectare a înfasurarilor fazelor motorului si de tipul comenzii.
Din acest punct de vedere exista trei categorii de MPP: inductoare, reactive inductor-reactive.
MPP inductoare cu excitatie independenta de la magneti permanenti (de tip electromagnetic) se obtin prin înlocuirea bobinelor înfasurarii de excitatie cu magneti permanenti.
Relatia
dintre ![]() , l, m este :
, l, m este :
![]() (1)
(1)
În
care k=0, 1, 2... este un numar întreg oarecare, iar 0<a<m/2, astfel
ca m si a sa fie prime între ele. Valorile posibile ale lui m, a
si ![]() sunt date în tabelul de mai jos , pentru
diferite valori ale numarului de faze m = 3,.,9.
sunt date în tabelul de mai jos , pentru
diferite valori ale numarului de faze m = 3,.,9.
|
M |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
q(3k |
q(4k |
q(5k q(5k |
q(6k |
q(7k q(7k q(7k |
q(8k q(8k |
q(9k q(9k q(9k |
Semnul
din fata lui a determina sensurile de rotatie a rotorului
MPP fata de sensul de succesiune a fazelor alimentate. Sensurile
coincid pentru a pozitiv impar sau negativ par si sunt inverse în
cazurile celelalte. Pentru a evita aparitia fortelor de atractie
unilaterala a rotorului în timpul functionarii, se ia a
maxim pentru m > 4. În acest fel numarul a se poate
interpreta ca fiind numarul de zone de faza aflate în câmp pe durata
dintre doua tacturi de comanda. Pentru exemplul din figura 6 s-au
luat l = 8, m = 4, q = 2, k = 6. Rezulta
![]() = 8 x 6 + 2 = 50.
= 8 x 6 + 2 = 50.
|
Fig. 6 |
MPP cu excitatie
independenta sunt acelea la care circuitul de excitatie este separat
fizic si este alimentat de la o sursa proprie de tensiune
continua (fig.6). Fluxul constant de excitatie nu mai este creat de
componenta homopolara directa a curentului de faza, ca în cazul
MPP inductoare cu autoexcitatie si prin urmare, motorul se va
alimenta cu impulsuri de polaritate alternativa. Alimentarea cu impulsuri
de aceeasi polaritate ar satura inutil motorul, prin existenta
componentei homopolare directe a curentului. Pentru a bloca aparitia
fluxului de autoexcitatie, trebuie evitat cuplajul magnetic între faze.
Aceasta se face prin legarea a doua înfasurari pe o
faza, corespunzatoare la permeante magnetice decalate cu ![]() radiani electrici.
radiani electrici.
2.2 MPP inductor-reactive
MPP de acest tip au un rotor pasiv dintat, la care înfasurarile fazelor statorice sunt legate astfel încât sa se elimine cuplajul magnetic dintre faze. În cazul MPP monostatorice acest lucru se realizeaza prin legarea a doua înfasurari corespunzatoare la doi poli diametral opusi, cu permeante egale si aceeasi orientare magnetica. Din punct de vedere functional MPP reprezentat în figura 6 poate fi considerat un MPP inductor-reactiv.
În cazul alimentarii fazelor cu impulsuri de aceeasi polaritate, apare atât componenta homopolara directa cât si cea inversa, ceea ce face ca motorul sa dezvolte atât cuplu activ cât si cuplu reactiv. În mod norma,l cele doua cupluri sunt antagoniste, cel reactiv fiind mai mic. Pentru a mari componenta activa se recomanda o secventa de alimentare monopolara, cu mai multe faze alimentate simultan.
Pentru m = 4 faze, se prefera alimentarea a 2 faze cu impulsuri de aceeasi polaritate. Prin alimentare cu impulsuri de polaritate alternanta dispare componenta homopolara directa, deci si cuplul activ, motorul dezvoltând numai cuplu reactiv, de valoare mai mica.
Din punct de vedere constructiv, aceste MPP pot fi monostatorice sau polistatorice. La constructiile monostatorice l = 2m, iar configuratia dintilor este similara celei expuse la MPP inductoare. Lipsa cuplajului între faze le situeaza în aceeasi clasa cu tipurile polistatorice. Un exemplu de MPP inductor-reactiv polistatoric cu trei faze dispuse pe trei statoare separate din punct de vedere magnetic a fost prezentat in figura 5.
2.3 MPP reactive
|
Fig.7 |
Bobinele statorice sunt astfel legate încât sa nu apara componenta homopolara directa a fluxului, adica nu exista practic flux de excitatie constant, deci motorul nu dezvolta cuplul activ. În figura 7 este prezentata o sectiune schematica printr-un MPP de tip reactiv.
1.3 Marimi caracteristice ale MPP
1) Timpul de efectuare a unui pas ![]() . Se determina cunoscând variatia în timp a
unghiului de rotatie la efectuarea unui pas asa cum se arata în
figura 8. Tot din aceasta figura se poate determina frecventa
proprie de rezonanta (natural frequency) a motorului,
. Se determina cunoscând variatia în timp a
unghiului de rotatie la efectuarea unui pas asa cum se arata în
figura 8. Tot din aceasta figura se poate determina frecventa
proprie de rezonanta (natural frequency) a motorului, ![]() .
.
|
Fig. 8 |
2) Unghiul de pas (step angle) ![]() este unghiul de rotatie pe care îl
executa rotorul la aplicarea unui impuls de comada.
este unghiul de rotatie pe care îl
executa rotorul la aplicarea unui impuls de comada.
3) Unghiul dinamic de sarcina (dynamic load angle) ![]() reprezinta
devierea unghiulara maxima a pozitiei rotorului fata de punctul de echilibru stabil,
dupa aplicarea ultimului impuls de comanda. Uneori este denumit
si suprareglare (overshoot).
reprezinta
devierea unghiulara maxima a pozitiei rotorului fata de punctul de echilibru stabil,
dupa aplicarea ultimului impuls de comanda. Uneori este denumit
si suprareglare (overshoot).
4) Unghiul static de sarcina (angular displacement under static
load) ![]() (fig. 13)
reprezinta unghiul ce defineste deplasarea punctului de echilibru
stabil, datorita cuplului rezistent pe arborele motorului. Acest unghi se
mai numeste si deviatie.
(fig. 13)
reprezinta unghiul ce defineste deplasarea punctului de echilibru
stabil, datorita cuplului rezistent pe arborele motorului. Acest unghi se
mai numeste si deviatie.
5) Cuplul maxim static sincronizant (holding
torque) ![]() este
egal cu valoarea maxima a cuplului rezistent de tip activ, care poate fi
aplicat la arborele motorului, având o faza alimentata,
fara ca sa se produca o rotatie continua a
rotorului.
este
egal cu valoarea maxima a cuplului rezistent de tip activ, care poate fi
aplicat la arborele motorului, având o faza alimentata,
fara ca sa se produca o rotatie continua a
rotorului.
|
Fig. 9 |
6) Cuplul de mentinere (detent torque) ![]() este egal
cu cuplul rezistent maxim, ce poate fi aplicat la arborele unui MPP cu fazele
nealimentate, fara ca sa provoace rotirea continua a
rotorului. Este caracteristic MPP cu magneti permanenti.
este egal
cu cuplul rezistent maxim, ce poate fi aplicat la arborele unui MPP cu fazele
nealimentate, fara ca sa provoace rotirea continua a
rotorului. Este caracteristic MPP cu magneti permanenti.
8) Caracteristica de mers (slew curve) defineste domeniul cuplu-frecventa de comanda limita, în care MPP poate functiona în regim stabilizat, fara pierderi de pasi. Caracteristica este ridicata pentru un moment de inertie dat.
|
Fig. 10 |
9) Frecventa limita de pornire (maximum start-stop stepping rate) reprezinta frecventa maxima a impulsurilor de comanda, cu care MPP poate porni fara pierderi de pasi, pentru un cuplu rezistent si un moment de inertie date. Aceasta frecventa rezulta din caracteristica de pornire.
10) Cuplul limita de pornire (maximum start-stop torque) reprezinta cuplul rezistent maxim la arbore cu care MPP poate porni, la o frecventa de comanda si un moment de inertie date, fara pierderi de pasi.
11) Frecventa limita de mers (maximum slew stepping rate) reprezinta frecventa maxima cu care poate functiona un MPP, pentru un cuplu rezistent si un moment de inertie date.
12) Cuplul limita de mers (maximum torque at maximum slew stepping rate) reprezinta cuplul rezistent maxim cu care poate fi încarcat un MPP, la un moment de inertie dat si o frecventa de comanda cunoscuta.
13) Puterea la arbore (power output for maximum torque at slew stepping rate) este puterea utila la arborele motorului, corespunzatoare punctului de functionare de pe caracteristica de mers, caracterizat de cuplul limita de mers si de frecventa maxima de mers.
14)
Eroarea de pas (stepping error) ![]() , reprezinta abaterea unghiulara sistematica
maxima, pozitiva sau negativa, fata de valoarea
unghiulara nominala a pasului; este necumulativa.
, reprezinta abaterea unghiulara sistematica
maxima, pozitiva sau negativa, fata de valoarea
unghiulara nominala a pasului; este necumulativa.
15) Precizia de pozitionare cu MPP depinde, în esenta, de eroarea unghiulara sistematica (eroarea de pas) a motorului folosit. În general, precizia de pozitionare este privita ca un rezultat al functionarii în ansamblu a sistemului de pozitionare incremental, caz în care se poate constata ca eroarea cu care se executa incrementul de pozitionare depinde si de sistemul de transmisie a miscarii dintre motor si elementul pozitionat. Precizia de pozitionare este influentata astfel de eroarea de divizare a pasului prin sistemul de transmisie, de jocul în lagare si în cuplaje, precum si de caracteristicile dinamice ale sarcinii.
2. Determinarea momentului de inertie redus la arborele motorului. Determinarea momentului rezistent redus la arborele motorului.
Reducerea momentelor de inertie si rezistent la arborele motorului se face tinand cont de datele initiale si de particularitatile constructive ale sistemului de actionare.
Calculul momentului de inertie redus:
In forma sa cea mai generala momentul de inertie redus se calculeaza cu ajutorul formulei:
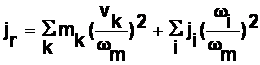
unde
elementele "k" realizeaza miscare de translatie fiind caracterizate de masa m si viteza v
elementele "i" realizeaza miscare de rotatie fiind caracterizate de momentul de inertie j si viteza unghiulara v
In cazul sistemului de actionare din proiect exista doar elemente cu
miscare de rotatie ceea ce inseamna ca din formula principala vor ramane doar termenii ce caracterizeaza corpurile care au o miscare de rotatie(termenii "i")
Pentru calculul momentului de inertie redus se considera ca rotile dintate ale sistemului de actionare sunt realizate din otel a carui densitate este r=7800 kg/m2
Tinand cont de datele furnizate de proiect se calculeaza mai intai razele rotilor dintate din componenta sistemului de actionare aplicand relatia:
![]()
unde
r este raza rotii dintate
m este modulul rotii dintate
z este numarul de dinti al rotii dintate
Aplicand formula pentru fiecare roata se obtine:

Pentru cuplajul elastic se cunoaste raza interioara care este jumatate din diametrul arborelui de iesire al motorului. Diametrul exterior si masa se adopta, in cazul primului tinand cont de considerente de gabarit iar in al doilea caz tinand cont de materialul din care este realizat cuplajul. Datele caracteristice cuplajului elastic sunt prezentate mai jos:
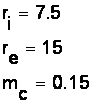
Odata razele rotilor calculate se poate trece la calculul maselor acestora aplicand relatia:
![]()
unde
m este masa
r este densitatea materialului rotii dintate
V volumul rotii dintate
Tinand cont de acest lucru se calculeaza masa pentru fiecare din cele patru roti:

Urmatoarea etapa este calculul momentului de inertie al cuplajului care se calculeaza dupa principiul unui cilindru tubular:
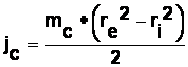
Adica
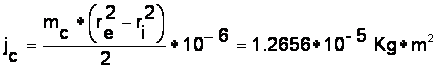
Pentru calculul momentului de inertie redus este necesar sa cunoastem vitezele unghiulare ale elementelor antrenate de motorul electric pas cu pas.
Viteza unghiulara a motorului se calculeaza pornind de la frecventa de pasi si valoarea pasului motorului, astfel:
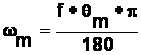
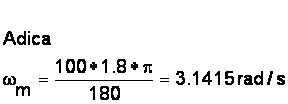
Datorita particularitatilor mecanismului planetar vitezele unghilare se calculeaza prin metoda imobilizarii bratului port-satelit prin rotire a rotii fixe cu aceiasi viteza dar in sens invers satelitului:
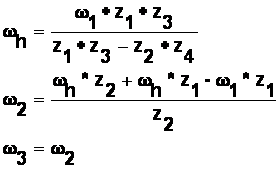
Inlocuind in relatii datele cunoscute se obtin urmatoarele valori:
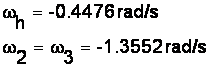
Cu toate datele obtinute anterior se calculeaza momentul de inertie redus la arborele motorului, care in cazul nostru are urmatoarea forma:
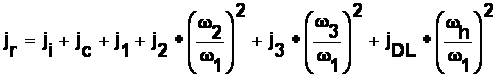
Calculul momentului rezistent redus :
Se pleaca de la momentul rezistent al dispozitivului actionat care este specificat in tema de proiect:
Datorita particularitatilor mecanismului planetar momentul rezistent redus la arborele motorului este:
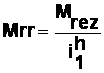
unde
Mrez este momentul rezistent al dispozitivului de lucru
i1h este raportul de transmitere de la roata 1 la bratul port-satelit H
Raportul de transmitere i1h se calculeaza cu relatia:
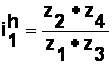
Inlocuind in relatiile de mai sus datele se obtine ca:
![]()
Pentru verificarea datelor obtinute s-a realizat programul jred.m in mediul de lucru Matlab. Programul este listat mai jos:
function jred
z1=input('Numarul de dinti pentru roata 1: ');
z2=input('Numarul de dinti pentru roata 2: ');
z3=input('Numarul de dinti pentru roata 3: ');
z4=input('Numarul de dinti pentru roata 4: ');
b=input('Latimea rotilor[mm]: ');
m1=input('Modulul rotilor 1 si 2[mm]: ');
m2=input('Modulul rotilor 3 si 4 [mm]: ');
jdl=input('Momentul de inertie al dispozitivului de lucru[Kg*m^2]: ');
ji=input('Momentul de inertie rotoric [Kg*m^2]: ');
ro=2700;
omega1=3.1415;
r1=(m*z1)/2;
r2=(m*z2)/2;
r3=(m*z3)/2;
rci=7.5;
rce=20.5;
m1=ro*pi*r1^2*b*10^-9;
m2=ro*pi*r2^2*b*10^-9;
m3=ro*pi*r3^2*b*10^-9;
mc=0.25;
j1=(m1*r1^2*10^-6)/2;
j2=(m2*r2^2*10^-6)/2;
j3=(m3*r3^2*10^-6)/2;
jc=(mc*(rce^2-rci^2)*10^-6)/2;
i12=z2/z1;
i1h=z2*z4/(z1*z3);
omegah=(omega1*z1*z3)/(z1*z3-z2*z4);
omega2=(omegah*z2+omegah*z1-omega1*z1)/z2;
omega3=omega2;
jr=ji+jc+j1+j2*omega2^2/omega1^2+j3*omega3^2/omega1^2+jdl*omegah^2/omega1^2
Mr=0.02;
La rularea programului se obtin urmatoarele rezultate care confirma corectitudinea calculelor anterioare:
>> jred
Numarul de dinti pentru roata 1: 22
Numarul de dinti pentru roata 2: 87
Numarul de dinti pentru roata 3: 36
Numarul de dinti pentru roata 4: 73
Latimea rotilor[mm]: 4
Modulul rotilor[mm]: 2
Momentul de inertie al dispozitivului de lucru[Kg*m^2]: 0.005
Momentul de inertie rotoric [Kg*m^2]: 0.00083
r1 = 22
r2 = 87
r3 =36
m1 =0.0474
m2 =0.7419
m3 =0.1270
mc =0.1500
j1 =1.1481e-005
j2 =0.0028
j3 =8.2316e-005
jc =1.2656e-005
i12 =3.9545
i1h = 8.0189
omegah =-0.4476
omega2 = -1.3552
omega3 = -1.3552
jr =0.0015
Mr =0.0200
Functia se aplica pentru cele trei tipuri de motoare obtinandu-se urmatoarele date :
|
Motorul |
Momentul de inertie redus[N*m] |
Momentul rezistent redus[N*m] |
|
HY200-4288 |
|
|
|
HY200-4270 |
|
|
|
HY200-4247 |
|
|
3.Modelarea matematica a functionarii sistemului in regim
dinamic
In sistemele de actionare specifice mecatronicii (care presupun conditii de precizie dosebita) durata regimului tranzitoriu este aproximativ egala cu durata de regim. In cele mai multe cazuri comportarea dinamica a sistemului de actionare in regim tranzitoriu este foarte importanta ea furnizand informatii despre timpii caracteristici si stabilitatea sistemului.
Pentru calculul regimului dinamic se construieste un model matematic:
Se considera ca orice magnet poate fi înlocuit cu o înfasurare fictiva. Daca avem un motor cu m faze, atunci acesta va fi deservit de m+1 circuite electrice (m circuite de comanda pentru fiecare faza la care se adauga circuitul electric principal). Analogia mecanic - electric se face considerând un sistem unitar cu m+2 coordonate generalizate (câte o ecuatie pentru fiecare dintre cele m faze la care se adauga o ecuatie de miscare si o ecuatie a circuitului electric principal).
Modelul matematic este de forma de mai jos:
![]()
unde
- U este matricea tensiunilor pe faza: 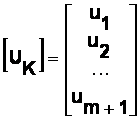
-
R este matricea rezistentelor pe faza: 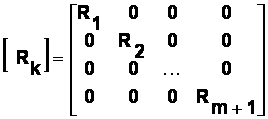
- I este matricea curentilor pe faza si pe circuitul
principal: 
- matricea fluxurilor 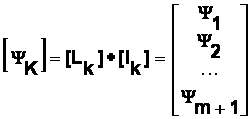
In cazul particular al motorului din proiect numarul de faze m = 2 sunt denumite a si respectiv b. Se considera ambele faze alimentate simultan. In acest caz, particularizand modelul matematic de mai sus, se pot scrie urmatoarele relatii:
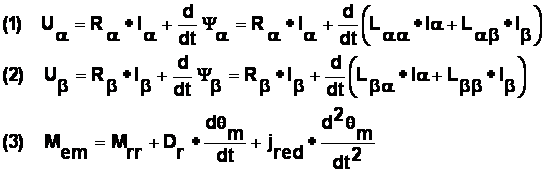
unde:
Laa, Lbb sunt inductivitati proprii fazei si Lab Lba sunt inductivitati mutuale
um unghiul de pas cu care se roteste arborele motorului
Dr este coeficientul de frecare uscata
Mem este cuplul electromagnetic
Daca se lucreaza in camp magnetic saturat, ceea ce presupune ca inductivitatile fie ele proprii sau mutuale depind atat de unghiul de pad cat si de curent. Din pacate dependenta inductivitate - curent este greu de demonstrat, ea probandu-se in general prin masuratori.
Daca se lucreaza in camp magnetic nesaturat se considera ca inductivitatile depind numai de unghiul de pas (um). Curentii pe faza in acest caz variaza in functie de timp.
Ne intereseaza cum variaza in timp curentii , precum si acceleratia si viteza unghiulara in faza de pornire.
Pentru o mai mare usurinta in prelucrarea datelor primele doua ecuatii se pot rezolva matricial. Se poate vorbi astfel de o matrice a inductivitatior, a derivatelor acestora, o matrice a tensiunilor, o matrice a curentilor si a variatiilor curentilor.

Matricile intalnite in modelul matematic general se particularizeaza pentru cazul motorului pas cu pas din proiect (motorul MDP HY200-4288) alimentat cu doua faze.
matricea inductivitatilor
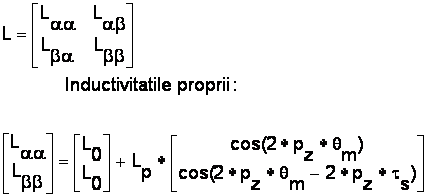
Inductivitatile mutuale:
![]()
unde:
- L0 este inductanta pe faza L0=0.0022H
- Lp este inductanta medie pe faza Lp=0.00005H
- pz este numarul de dinti rotorici pz=25
ts este unghiul între doi poli statorici consecutivi ts p
matricea variatiilor
inductivitatilor (in raport cu unghiul de pas) 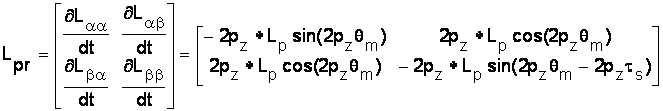
matricea tensiunilor pe faza
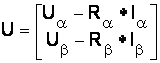
matricea curentilor pe faza
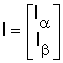
Pentru rezolvarea acestui sistem de ecuatii diferentiale se apeleaza la metoda Runge - Kutta. Pentru rezolvarea sistemului de ecuatii diferentiale s-a utilizat mediul de lucru Matlab 6. Metoda de rezolvare aleasa este Runge-Kutta, existenta în mediul de lucru prin functia ODE 23. Metoda consta în integrarea unui sistem de ecuatii diferentiale pe un interval de timp cuprins între t0 si t1, tinându-se seama de conditiile initiale a caror valori sunt date de vectorul Y0. ODE 23 returneaza o matrice în care:
-prima coloana contine punctele la care este evaluata;
-coloanele ramase contin valorile corespondente ale solutiei si primele sale n-1 derivate.
Spre deosebire de alte metode , care integreaza în pasi de marime egala pentru a ajunge la o solutie , ode 23 examineaza cât de repede o solutie se schimba si adapteaza marimea pasilor sai corespunzator. Ode 23 va folosi pasi de marime neuniforma intern când rezolva ecuatia diferentiala, dar va returna solutia în puncte distantate egale.
Sistemul de ecuatii diferentiale este cuprins in functia ecdifRK.m care furnizeaza vectorul de necunoscute functiei ode23
function yp=ecdifRK(t,y)
Dr=0.001;
jr=0.0015;
Mrr=0.0025;
I=8.9;
R=0.3;
Ua=I*R;
Ub=Ua;
pz=25;
taus=pi/2;
L0=2.2*10^-3;
Lp=0.05*10^-3;
Lab=Lp*sin(2*pz*y(3));
Lba=Lab;
L=[L0;L0]+Lp*[cos(2*pz*y(4));cos(2*pz*y(4)-2*pz*taus)];
Laa=L(1,1);
Lbb=L(2,1);
Laaprim=-2*pz*Lp*sin(2*pz*y(4));
Labprim=2*pz*Lp*cos(2*pz*y(4));
Lbaprim=Labprim;
Lbbprim=-2*Lp*pz*sin(2*pz*y(4)-2*pz*taus);
L=[Laa Lab;Lba Lbb];
U=[Ua-R*y(1);Ub-R*y(2)];
Lprim=[Laaprim Labprim;Lbaprim Lbbprim]';
I=[y(1);y(2)];
yp(4)=y(3);
x=(L^-1)*U-(L^-1)*Lprim*I*yp(4);
yp(1)=x(1);
yp(2)=x(2);
yp(3)=0.5*(y(1)^2*Laaprim+y(2)^2*Lbbprim)/jr +y(1)*y(2)*Labprim/jr-Dr/jr*yp(4)-Mrr/jr;
yp=[yp(1) yp(2) yp(3) yp(4)]';
Vectorul necunoscutelor furnizate de functia ecdiRK.m este preluat de functia ode23.m care este echivalentul in Matlab al algoritmului Runge-Kutta. Functia ode23.m va furniza rezultatele sub forma numerica.
Functia solutii.m va apela ode23.m si va interpreta in mod grafic rezultatele obtinute.
function solutii
[t,y]=ode23(@ecdifRK,[0 2],[0,0,0,0]);
subplot(2,2,1);plot(t,y(:,1));
grid;
ylabel('Ia[A]');
xlabel('timp[s]');
subplot(2,2,2);plot(t,y(:,2));
grid;
ylabel('Ib[A]');
xlabel('timp[s]');
subplot(2,2,3);plot(t,y(:,3));
grid;
ylabel('viteza unghiulara (omega)[rad/s]');
xlabel('timp[s]');
subplot(2,2,4);plot(t,y(:,4));
grid;
ylabel(' unghiul motor (teta)[rad]');
xlabel('timp[s]')
Functia solutii.m va furniza patru grafice care surprind variatia necunoscutelor in functie de timp respectiv:
Ia = f(t) variatia in timp a curentului pe faza alfa
Ib = f(t) variatia in timp a curentului pe faza beta
e= f(t) variatia intimp a acceleratiei unghiulare
v= f(t) variatia in timp a vitezei unghiulare
Solutiile furnizate de functia solutii.m pentru datele proiectului pentru cele trei motoare sunt prezentate in figura de mai jos:
Motorul 1- HY200-4288
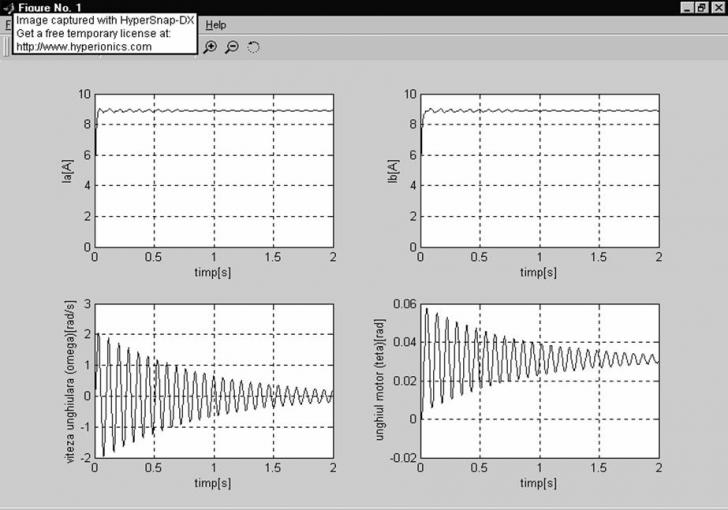
Motorul 2 HY200-4270
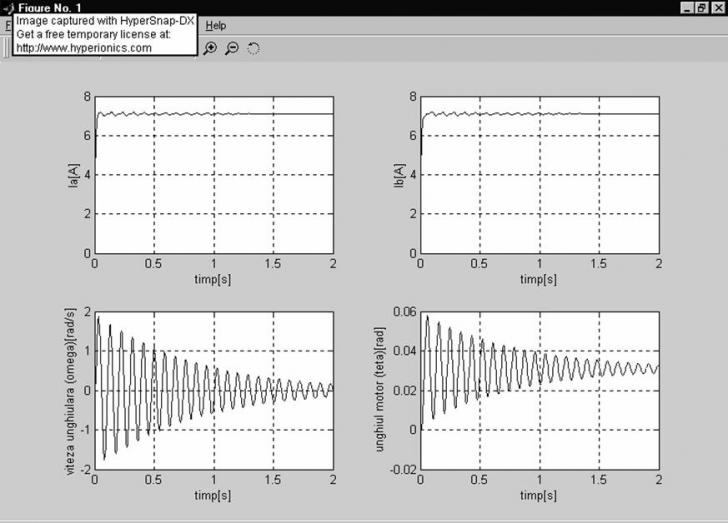
Motorul 3 HY200-4247
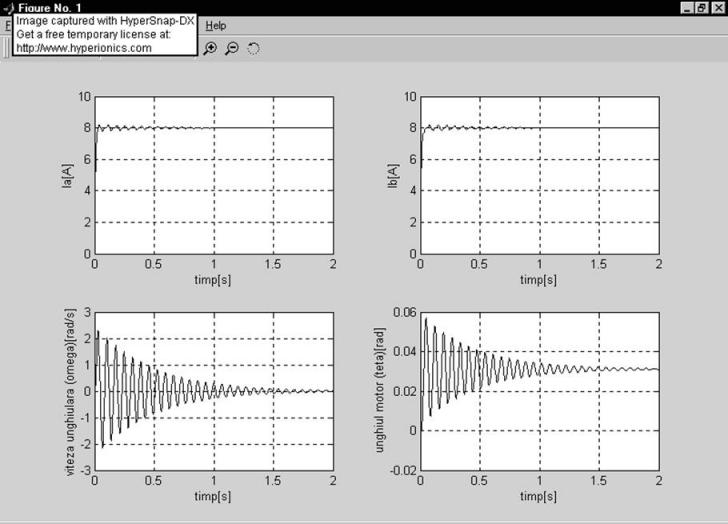
In figurile de mai sus sunt prezentate graficele ce descriu modul de variatie în regim tranzitoriu de pornire a celor patru marimi ce caracterizeaza functionarea unui motor pas cu pas cu doua faze, si anume:
curentul de excitatie pe faza intai (alfa)
curentul de excitatie pe faza a doua (beta)
viteza unghiulara a arborelui de iesire (omega)
acceleratia unghiulara a arborelui de iesire (epsilon)
Din graficele de mai sus se observa ca in vreme ce motoarele 1 si 2 au nevoie de un timp mai indelungat sa se stabilizeze, motorul 3 are un regim tranzitoriu satisfacator ceea ce il face cel mai eligibil.
Datorita frecarilor de natura statica cat si a fenomenelor de saturatie ale campului magnetic exista patru zone de functionare in regim tranzitoriu. Se pot calcula timpii caracteristici sistemului de actionare in regim tranzitoriu.
Motorul 1
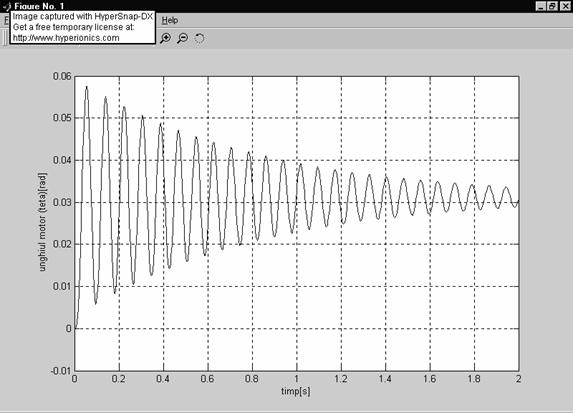
Motorul 2
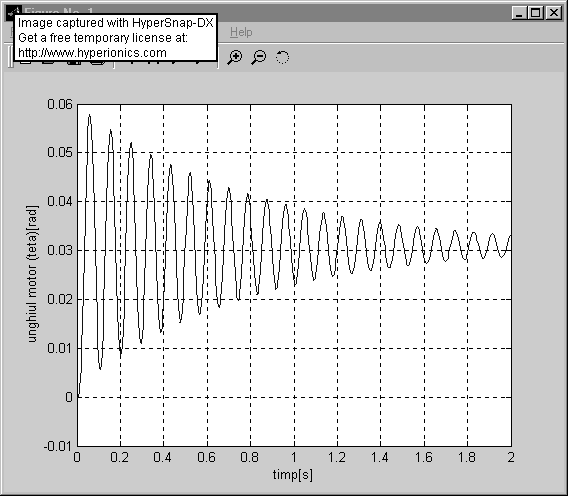
Motorul 3
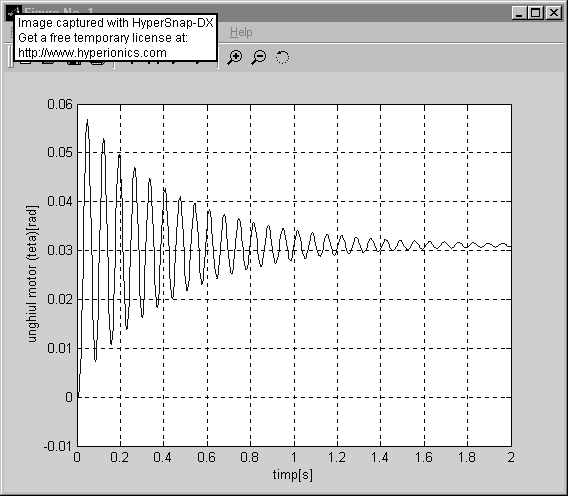
Timpii caracteristici :
timpul de prima stabilire reprezinta intervalul masurat din momentul inceperii pornirii pana cand marimea de iesire este egela pentru prima data cu marimea stationara (1.8 grade) te1
timpul de crestere reprezinta timpul necesar pentru ca motorul sa execute o deplasare unghiulara egala cu 90% din valoarea stationara a deplasarii tc
timpul de incadrare initial reprezinta valoarea masurata de la inceputul procesului tranzitoriu pana in momentul in care parametrul se incadreaza pentru prima data in domeniul de toleranta admis tii
timpul de incadrare final reprezinta valoarea masurata de la inceputul procesului tranzitoriu pana in momentul in care parametrul se incadreaza definitiv in domeniul de toleranta admis tif
|
Motorul |
te [s] |
tc [s] |
tii [s] |
ti [s] |
|
HY200-4288 |
|
|
|
|
|
HY200-4270 |
|
|
|
|
|
HY200-4247 |
|
|
|
|
Devine evident faptul ca motorul cel mai bun pentru a satisface cerintele sistemului de actionare este motorul 3 HY200-4247 datorita comportarii superioare ca performanta in regim tranzitoriu fata de celelalte doua motoare.
Analizand graficele de variatie ale celor patru marimi caracteristice ale sistemului de actionare in regim dinamic se poate constata ca:
- curentul ia se stabilizeaza la valoarea de 8 [A] din catalogul motorului ales;
- curentul ib se stabilizeaza la valoarea de 8 [A] din catalogul motorului ales ;
- unghiul motor q se stabilizeaza la valoarea de 1.8 din catalogul motorului ales;
- viteza unghiulara w se stabilizeaza la zero;
Datorita faptului ca timpul de stabilizare a motorului 3 este satisfacator avand in vedere faptul ca dintre cele trei motare puse la dispozitie motorul 3 are cele mai bune performante se alege acesta din urma ca motor optim pentru sistemul de actionare electric. Toate calculele se vor raporta la parametrii motorului ales.
4. Simularea functionarii sistemului de actionare pentru comanda in
tensiune: treapta, rampa, sinusoidala
Pentru studiul functionarii in regim tranzitoriu, pentru aprecierea stabilitatii si fiabilitatii sistemului de actionare se simuleaza functionarea acestuia pentru diferite tipuri de semnal(tensiune) , mai precis treapta, rampa si sinusoidal. Simularea functionarii sistemului se face in mediul Matlab pe modulul Simulink care are ca principal domeniu de lucru studiul diferitelor sisteme in regim dinamic.
Simularea pleaca de la realizarea blocurilor de simulare. Datorita volumului mare de termeni al ecuatii pentru realizarea schemei de simulare se vor forma subsisteme care apoi se vor conecta in scopul obtinerii sistemului final.
Fundamentul matematic pe care se bazeaza simularea este acelasi ca si in cazul studiului in regim tranzitoriu. Practic trebuie reconstituite ecuatiile diferentiale care definesc caracteristicile dinamice ale sistemului de actionare.
Pentru liniarizarea calculului ecuatia diferentiala ce furnizeaza variatia curentilor de faza se descompune in doua ecuatii prin efectuarea operatiilor intre matricile componente. Astfel ecuatia:

Devine:

Simularea functionarii sistemului de actionare se va face considerand motorul ales,adica motorul 3 (HY200-4247)
Functionarea sistemului de actionare va fi simulata pentru trei tipuri de semnal in tensiune: treapta, rampa, sinusoidal
Schema de simulare pentru semnal treapta:
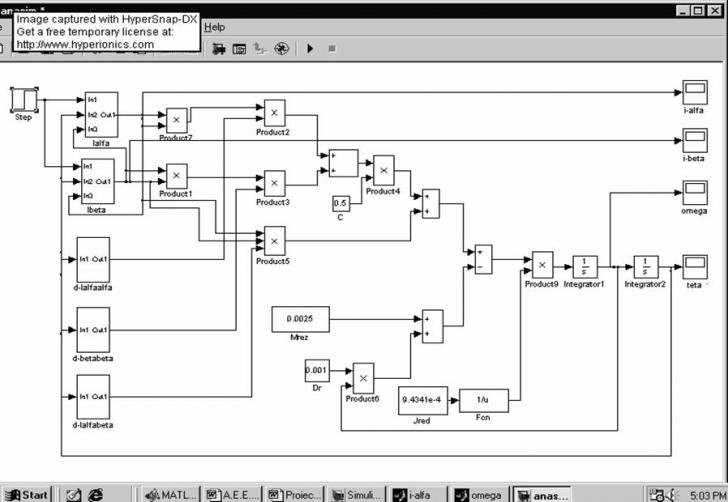
In urma simularii se obtin urmatoarele grafice:
- variatia in timp a curentului pe faza alfa
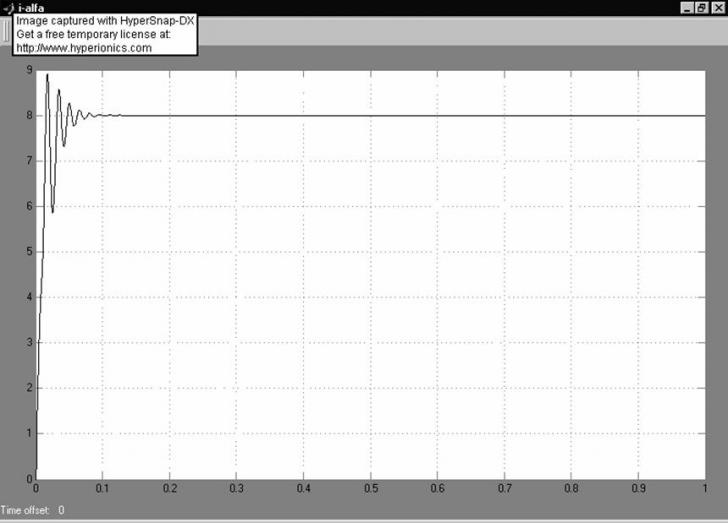
- variatia in timp a curentului pe faza beta
variatia in timp a vitezei unghiulare
variatia in timp a unghiului de comanda
Schema de simulare pentru un semnal rampa:
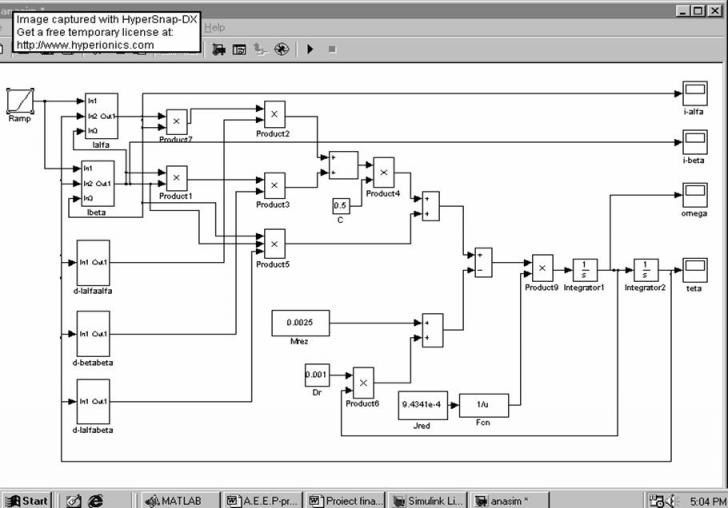
In urma simularii se obtin urmatoarele grafice:
- variatia in timp a curentului pe faza alfa
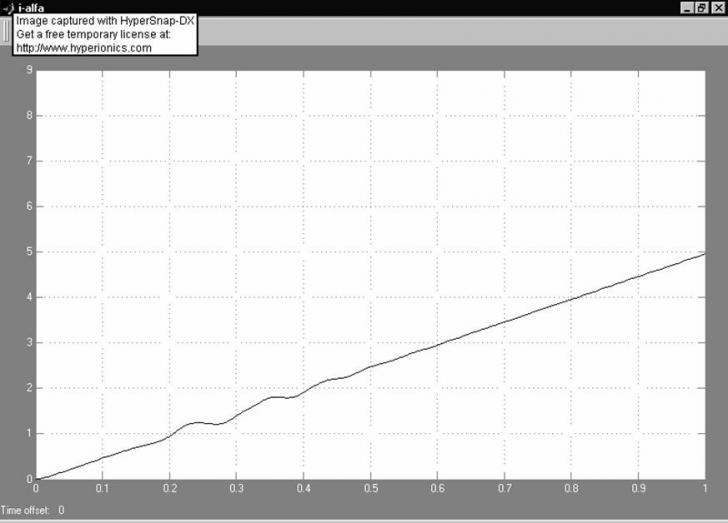
- variatia in timp a curentului pe faza beta
variatia in timpa vitezei unghiulare
variatia in timp a unghiului de comanda
Schema de simulare pentru un semnal sinusoidal:
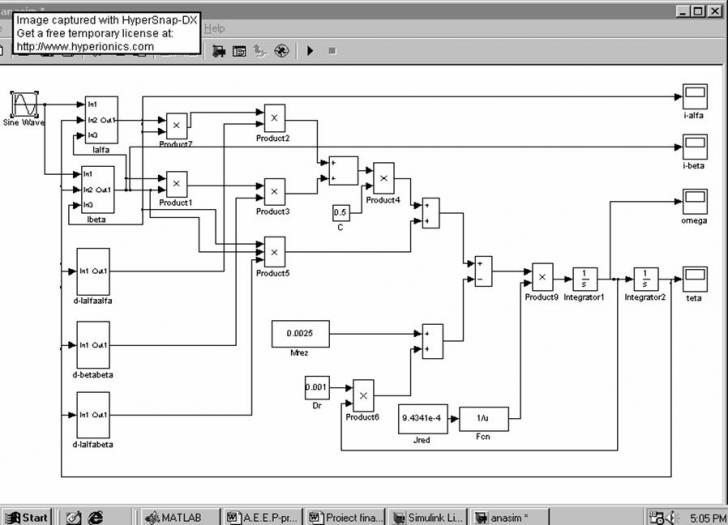
In urma simularii se obtin urmatoarele grafice:
- variatia in timp a curentului pe faza alfa
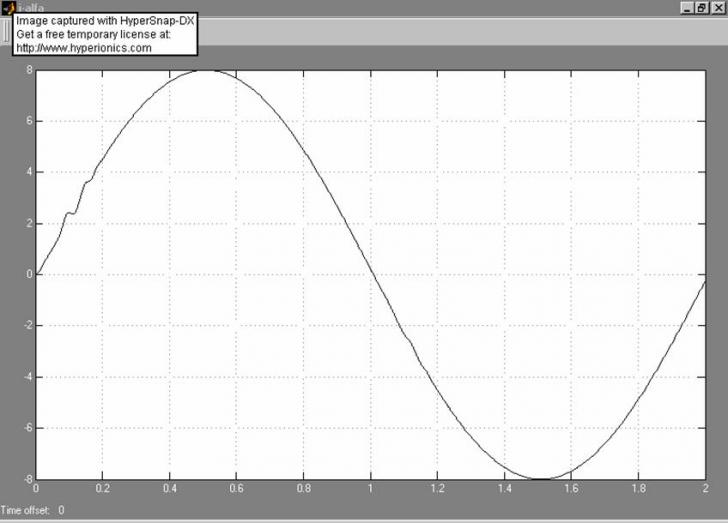
- variatia in timp a curentului pe faza beta
variatia in timpa vitezei unghiulare
variatia in timp a unghiului de comanda
Din graficele obtinute se pot trage aceleasi concluzii ca si in cazul studiului pe modelul matematic:
- curentul ia se stabilizeaza la valoarea de 8 [A] din catalogul motorului ales;
-curentul ib se stabilizeaza la valoarea de 8 [A] din catalogul motorului ales ;
-unghiul motor q se stabilizeaza la valoarea de 1.8 din catalogul motorului ales;
Se poate observa chiar o stabilizare mai rapida decat cea obtinuta prin metoda de aproximare Runge-Kutta
Din graficele de simulare rezulta ca motorul ales se integreaza armonios in sistemul de actionare conferind acestuia o functionare relativ lina. Se observa ca nu exista nici abateri fata de valorile din catalog ceea ce inseamna ca motorul are un randament foarte bun.
5. Studiul stabilitatii sistemului de actionare
Unul dintre cei mai importanti parametri, atunci cand vine vorba despre un sistem de reglare automata, este stabilitatea acestuia. Stabiliatatea presupune un echilibru reciproc al marimilor fizice (forte mecanice, cupluri, tensiuni, curenti, presiuni, etc.) care apar in timpul functionarii SRA.
Stabilitatea statica porneste de la premisa ca intr-un sistem de actionare pot exista o infinitate de astfel de regimuri actionate, corespunzator diferitelor valori ale perturbatiei (sau ale marimii de intrare), fiecare dintre ele reprezentând o stare de echilibru static.
Stabilitatea dinamica a sistemelor automate, reprezinta stabilitatea regimului tranzitoriu al acestora. Pentru a vedea daca un sistem de reglare automata este stabil trebuie analizat raspunsul y(t) (deci variatia în timp a parametrului reglat) pentru o perturbatie exterioara (sau o variatie a marimilor de intrare) limitata ca valoare.
Un sistem automat este stabil daca, dupa ce sub actiunea unei perturbatii exterioare (sau a unei vibratii la intrare ) îsi paraseste starea de echilibru stabil, el tinde sa revina în regimul stationar o data ce perturbatia dispare. Sau, altfel spus: într-un sistem stabil, o perturbatie momentana si limitata genereaza un raspuns amortizat.
Pentru un sistem instabil, raspunsul y(t) fie ca tinde la infinit îndepartându-se continuu de valoarea yst, fie ca executa oscilatii permanente în jurul valorii stationare a raspunsului, conducând din punct de vedere matematic la depasirea domeniului de valabilitate a ecuatiilor liniare, si fizic, în unele situatii, chiar la distrugerea obiectului reglarii.
Folosirea caracteristicilor de frecventa, amplitudine-pulsatie si faza-pulsatie (diagramele Bode) pentru evaluarea unui SRA permite, totodata determinarea rezervei de stabilitate a acestuia.
Rezerva de stabilitate a unui SRA se evalueaza prin doua marimi caracteristice si anume: rezerve de stabilitate în modul( numita si margine de amplitudine) si rezerva de stabilitate în faza (numita si margine de faza).
Se numeste margine de faza unghiul g definit de relatia g=180 grade +j w0) unde w0 reprezinta pulsatia critica (sau de taiere) la care amplitudinea( în decibeli) este nula. Pe locul de transfer pulsatia w0 este determinata în punctul unde hodograful intersecteaza cercul de raza unitara. Pe diagrama logaritmica, amplitudinea corespunzatoare pulsatiei w0 se determina la intersectia cu axa w (de aici si numele de pulsatie de taiere). Marginea de faza se masoara fie prin unghiul corespunzator punctului de intersectie între locul de transfer si cercul de raza 1, în sens trigonometric, fie pe diagrama faza-pulsatie, fata de dreapta j=-180 grade, la pulsatiile critice(w01, respectiv w
Sistemul automat este stabil daca marginea de faza este pozitiva(g > 0), iar rezerva de stabilitate se apreciaza în raport cu valoarea lui g. Valorile uzuale ale lui g sunt cuprinse între 20 si 30 grade. Pentru SRA cu raspuns bine amortizat se recomanda g=(30 grade .60grade).
Se numeste margine de amplitudine (sau amplificare, sau câstig) inversa valorii atenuarii la pulsatia wpi pentru care j=+180 grade. Astfel marginea de amplitudine mk se exprima în decibeli. Marginea de amplitudine este pozitiva daca mk>1, ceea ce înseamna |H(wpi)|<1 (punctul M1 sa fie la dreapta punctului -1,j0). Pe diagramele Bode, marginea de amplitudine se masoara la w wpi si este pozitiva dedesubtul axei w. Sistemul este stabil daca marginea de amplitudine este pozitiva. Valori uzuale pentru mk în cazul unui SRA cu amortizare buna sunt mk =10.20dB.
Criteriul Bode reprezinta transpunerea la scara logaritmica a criteriului Nyquist simplificat. El se exprima astfel:
Conditia necesara si suficienta ca un sistem de reglare automata sa fie stabil este ca reprezentarea faza-pulsatie sa intersecteze axa w într-un punct situat dupa intersectia cu aceeasi axa a reprezentarii amplitudine-pulsatie (deci wpi> w
Ne propunem în cele ce urmeaza sa utilizam criteriul anterior mentionat, pentru a determina stabilitatea sistemului de actionare ales la capitolul anterior, pentru aceasta vom utiliza mediul de simulare SIMULINK si anume schema de mai jos, formata din urmatoarele blocuri:
Generator semnal de tip de functie treapta;
Functia de transfer a motorului data de relatia:
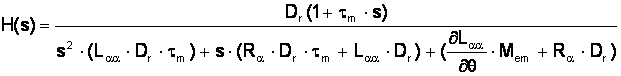
Analizor de spectru.
Elementele care intervin în functia de transfer sunt:
Dr = coeficientul de frecare vâscoasa
tm = Jm/Dr
Ra = rezistenta pe o faza
Laa= inductivitatea proprie Laa=L0+Lp cos(50 q q cos(p
Sistemul este stabil daca marginea de faza si marginea de amplitudine sunt pozitive. Rezerva de stabilitate se apreciaza in functie de valoarea lui g (marginea de faza), care are urmatoarea formula:
![]()
Rezerva de stabilitate se apreciaza in functie de valoarea lui g. Marginea de amplitudine:
![]()
Pentru a putea fi simulata functia de transfer se calculeaza parametrii acesteia:
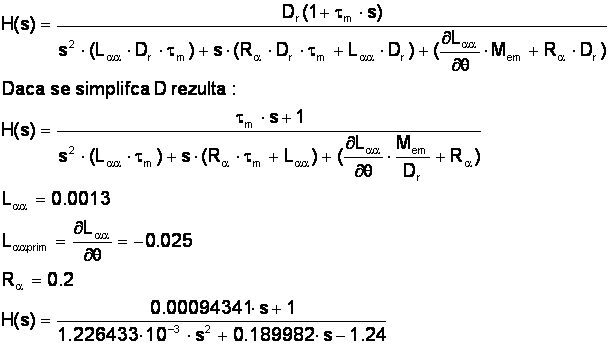
Schema de simulare a functiei de transfer este:
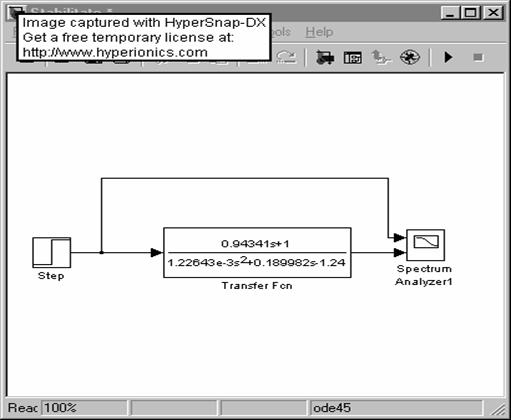
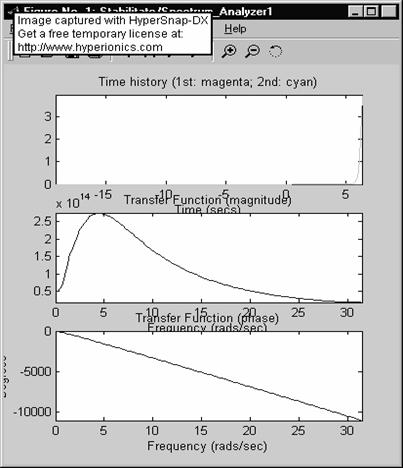
In urma simularii se obtine diagrama Bode:
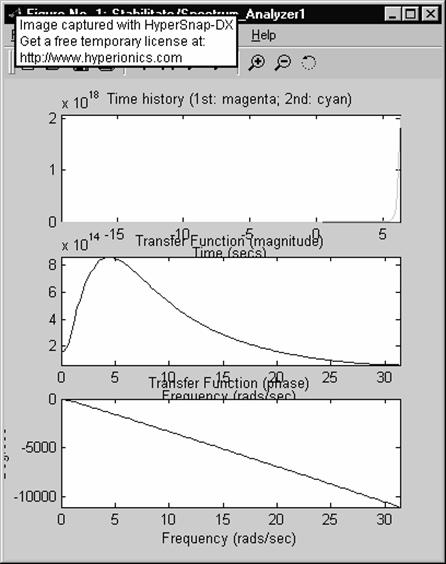
Din analiza spectrului se observa o variatie a fazei care se incadreaza in criteriul de stabilitate. In cazul amplitudiinii tendinta este buna dar curba nu se integreaza in norma de stabilitate deoarece marginea de amplitudine tinde la 0 dar nu este pozitiva.
Pentru a putea afla cauzele instabilitatii sistemului se calculeaza polii functiei de transfer. Calculul este facut in fereastra de comanda Matlab:
>> roots([1.22643e-3 0.189982 -1.24])
ans =
Conform teoriei stabilitatii sistemului o cauza a instabilitatii este existenta unui pol pozitiv. Influenta polului pozitiv poate fi anulata prin utilizarea unui regulator PID ( proportional - integrativ - derivativ).
Schema de studiu al stabilitatii devine:
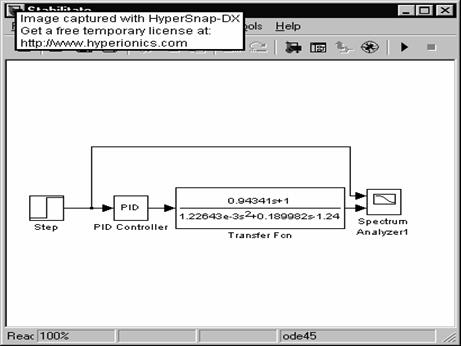
Blocul functional PID din Simulink are urmatoarel particularitati:
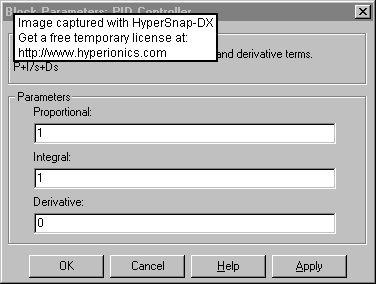
Rezulta ca functia de transfer a unui regulator PID este:
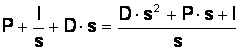
Aceasta functie trebuie particularizata astfel incat sa anuleze polul pozitiv care provoaca instabilitatea sistemului. Parametrii regulatorului se determina pornind de la relatia in bucla deschisa a sistemului de reglare automata:
![]()
Functia de transfer a regulatorului poate fi pusa in cazul cel mai general sub forma:
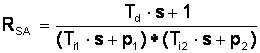
unde
Td, Ti1, Ti2, - timpi caracteristici ai SA
p1, p2 - polii functiei de transfer a sistemului
Presupunem ca polul pozitiv este p2. Functia de transfer pe care regulatorul trebuie sa o aiba este:
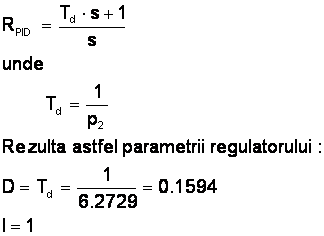
Acesti parametrii se introduc in caracteristicile regulatorului PID din schema de simulare a functiei de transfer. Se va obtine o noua diagrama Bode:
Comanda motorului electric pas cu p 22422p1524w as utilizand placa de achizitie de date
In prezent se intalnesc foarte frecvent situatii in care este necesara achizitionarea unor date privitoare la functionarea unui motor pas cu pas sau comanda acestuia prin intermediul calculatorului. Pentru a realiza conducerea motorului cu ajutorul calculatorului este nevoie de un program care sa contina un modul de comanda al motorului, de o placa de achizitie/comanda si de un bloc electronic de prelucrare.
Mediul in care se realizeaza comanda motorului pas cu pas este LabVIEW (de la National Instruments). Acest program are un modul foarte bine pus la punct dedicat achizitiei si transmisiei de date.
Placa de achizitie/comanda are rolul de a prelua semnalul de comanda de la calculator si de a o filtra si amplifica pentro ca apoi sa o tranmita blocului electronic.
Blocul electronic este necesar deoarece semnalele generate de placa nu au suficienta energie pentru a pune în miscare motorul, ele fiind, în general, semnale logice de comanda ( 0 - 5V), cu energie scazuta. Blocul electronic realizeaza comanda pe fiecare faza a motorului în conformitate cu semnalele primite de la placa. Blocul va avea un numar de circuite electronice de comanda pentru fiecare faza a motorului si un circuit electronic principal de coordonare. Pe lânga rolul electronic de comanda al motorului, blocul electronic realizeaza o amplificare (în tensiune sau curent, dupa necesitati) a semnalelor de comanda primite, furnizând motorului semnale electrice cu nivel energetic suficient de mare pentru a functiona.
Soft-ul de comanda al motorului a fost realizat într-o varianta simplificata, realizând un ciclu de functionare în care rotorul motorului se deplaseaza cu patru pasi. Se poate modifica numarul de cicluri de functionare dupa necesitate. Comanda motorului se opreste când s-a terminat de efectuat numarul de cicluri de functionare dorite sau se apasa butonul STOP, prevazut în fereastra Panel a soft-ului de comanda.
Un ciclu de functionare a motorului reprezinta o deplasare cu patru pasi a rotorului. Având în vedere ca se face o comanda digitala, fiecarei faze a motorului îi va fi asociat câte un bit de comanda în cadrul portului de iesire al placii de achizitie/comanda.Latimea portului este cea standard de 8 biti, dintre care vor fi folositi doar 4 (câte unul pentru fiecare faza a motorului). Succesiunea de comanda a motorului va fi (pentru un ciclu) :
|
Numarul pasi |
Faza 1 |
Faza 2 |
Faza 3 |
Faza 4 |
|
1 pas |
|
|
|
|
|
2 pasi |
|
|
|
|
|
3 pasi |
|
|
|
|
|
4 pasi |
|
|
|
|
Din punct de vedere teoretic comanda motorului se face prin intermediul unor impulsuri dreptunghiulare de durata cel putin egala cu perioada de stabilizare pentru a permite parametrilor sistemului de actionare sa-si atinga valorile de regim.
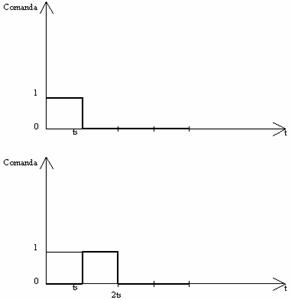
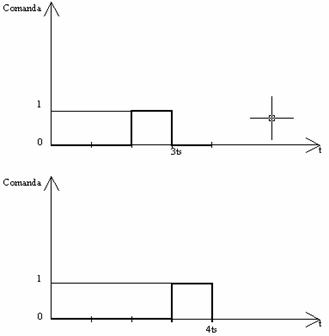
Pentru
comanda am folosit logica directa, unde 1 reprezinta comanda ,
iar 0 reprezinta lipsa comenzii.
Pentru realizarea comenzii motorului pas cu pas s-a realizat urmatoarea fereastra de comanda:
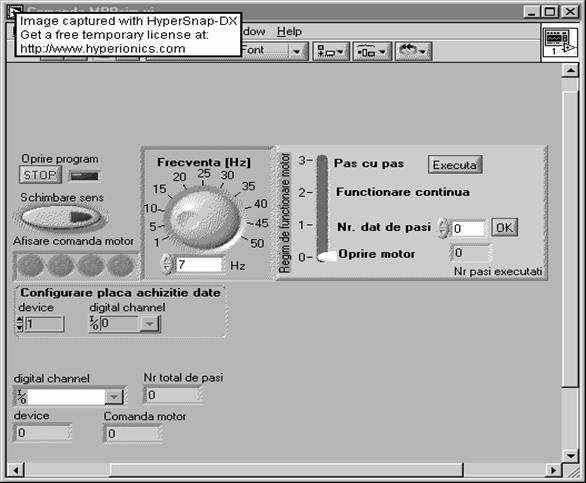
Diagrama de comanda a motorului pas cu pas:
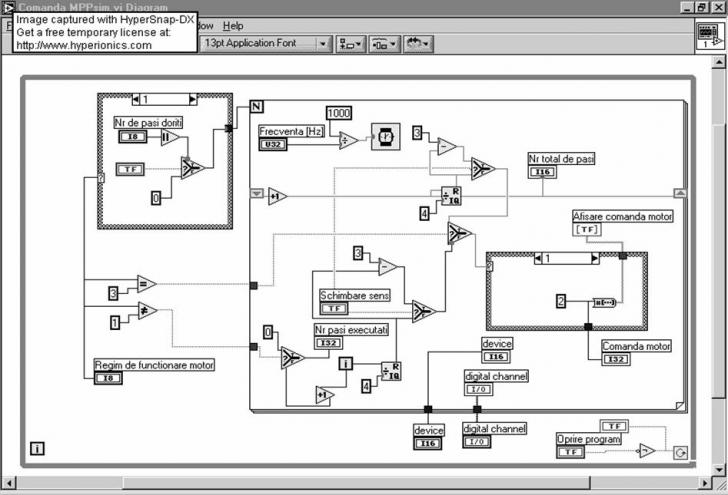
Programul prevede trei moduri de functionare a motorului:
pas cu pas - asteapta confirmarea utilizatorului pentru fiecare pas pe care il efectueaza
continua - asteapta de la programator doar acordul de start al motorului dupa care functioneaza continuu
numar finit de pas - efectueaza un numar de pasi furnizat de catre programator
Este prevazuta si posibilitatea opririi motorului din oricare din cele trei faze.
Pentru ca utilizatorul sa aiba un control total asupra functionarii sistemului blocul de comanda este introdus intr-o bucla WHILE care permite rularea programului atat timp cat utilizatorul nu actioneaza butonul de stop.
Pentru functionarea pas cu pas se executa procedura de comanda a unui pas o singura data dupa care programul se opreste si se asteapta o eventuala noua comanda.
Pentru functionarea continua se prevede realizarea procedurii de comanda pentru pas in continuu pana in momentul in care utilizatorul apasa butonul de stop, sau selecteaza un alt mod de lucru.
Pentru realizarea functionarii de un numar finit de pasi s-a apelat la o bucla de tip FOR care repeta procedura de comanda pentru un pas de un numar de ori stabilit de utilizator.
Programul prevede si inversarea sensului motorului care se face prin simpla selectare a unui buton.
De asemenea este prevazuta posibilitatea reglarii frecventei pasilor intr-un interval [0 - 50] Hz
Comanda de pas propriu-zisa este continuta in blocul SEQUENCE care are patru secvente - cate una pentru fiecare pas.
Programul acopera astfel o gama larga de necesitati putand fi adaptat unei game largi de necesitati.
|