Roboti Industriali Sisteme tentaculare

Sisteme tentaculare

13.1 Introducere

Configuratiile conventionale de roboti sunt mecanisme discrete obtinute prin legarea īn cascada a unor corpuri rigide articulate obtinute printr-o conexiune cu un singur grad de libertate. Mecanismul acestor structuri presupune existenta unor relatii cunoscute īntre centrele de greutate ale corpurilor articulate iar articulatiile sunt controlate prin legi de conducere proprii. Elementele lantului cinematic sunt formate din componente pasive, activarea fiind realizata numai la nivelul articulatiei.

Īn contrast cu structuri clasice, modelele de tip "tentacul", "trompa", "serpentina" sunt realizate prin conexiunea īn serie a unor elemente a caror miscare de īncovoiere (rotatie) este realizata dupa curbe continue. Aceasta ultima caracteristica desemneaza aceasta clasa de roboti ca "roboti continui", īn timp ce structurile conventionale sunt considerate ca "roboti discreti" [1].

Modelele de tip tentacul sunt formate, teoretic, dintr-un numar infinit de articulatii, ceea ce permite obtinerea unui lant cinematic descris printr-o curba continua si īi confera o mobilitate, ipotetic, infinita. Din acest motiv īn multe lucrari [2, 5] aceste modele sunt desemnate si ca modele "hiperredundante". Marea lor mobilitate face ca acesti roboti sa fie utilizati cu precadere īn spatii de operare cu restrictii deosebit de severe.

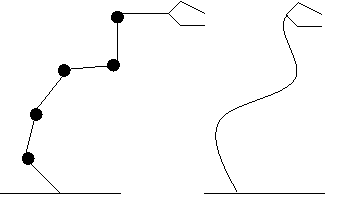
Figura 13.1 Model discret - model continuu

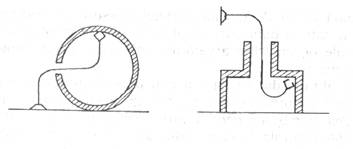
Īn acest fel se pot manipula piese, se pot realiza operatii de vopsire, sudura, eliminarea unor imperfectiuni tehnologice īn zone greu accesibile, containere īnchise, constructii tabulare, etc. (figura 13.2).

Figura 13.2   Model tentacular - aplicatii īn spatii cu restrictii

Proiectarea si realizarea unui sistem de tip tentacul ridica probleme complexe printre care am putea mentiona:

Dificultatea actionarii distribuite pe lungimea sistemului. Este evident ca o actionare electrica de tip clasic este inacceptabila datorita greutatii suportului magnetic. Mult mai pretabile pot fi actionarile de tip pneumatic, hidraulic sau cele care utilizeaza componente tehnologice noi, materiale inteligente de tip SMA, lichide ER, muschi artificiali din polimeri, etc.

Masurarea pozitiilor relative sau absolute a articulatiilor ridica probleme extrem de complexe. Īn noul curent se accepta masurarea unor puncte discrete, restul punctelor fiind obtinute prin proceduri speciale de estimare.

Dificultatea determinarii unei legi de miscare pentru īntreaga configuratie avāndu-se īn vedere complexitatea modelului matematic al tentaculului si al complicatiilor ce apar la implementarea unui controler distribuit.

13.2 Modele "tentacul"

Modele cu actionare intrinseca, la care sistemele de actionare se gasesc chiar īn structura corpului elementelor si constituie o componenta a mecanismului de animatie.

Modele cu actionare extrinseca īn care elementul activ este pozitionat īn afara structurii bratului iar miscarea este realizata printr-un mecanism de transfer (cabluri, fire, etc).

Modele hibride care utilizeaza ambele sisteme.

Fiecare dintre aceste grupe poate fi subdivizat īn modele planare sau spatiale dupa cum miscarea se produce īntr-un plan specificat, sau īn aria directiei din spatiu, respectiv.

13.2.1 Sisteme cu actionare intrinseca

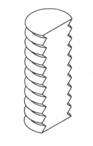
Cea mai simpla forma de actionare intrinseca este obtinuta din dispozitive planare fluidice de tipul celor prezentate īn figura 13.3.

Figura 13.3   Dispozitiv intrinsec planar

Figura 13.4 Model intrinsec spatial

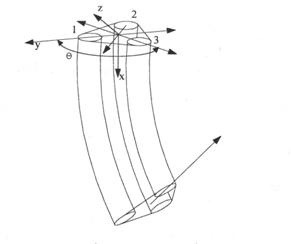
O schema simplificata a miscarii este prezentata īn figura 13.5. Pentru a obtine o anumita directie de rotatie se impune controlul strict al presiunii īn cele trei camere ale cilindrilor. O structura tentaculara completa este obtinuta prin legarea īn serie a cātorva module. Este evident ca, prin controlul distribuit al lantului de module, se obtine orientarea īn spatiul 3D si flexibilitatea formei īntregii structuri.

Figura 13.5 Miscarea modelului cu actionare spatiala

Figura 13.6 Robotul NOBEL MEC

O structura industriala cu actionare intrinseca, hidraulica, este oferita de terminalul robotului NOBEL MEC (figura 13.6). Fiecare element este actionat de un servosistem, comanda centralizata a acestora permitānd miscarea bratului īntr-un singur plan.

Figura 13.7 Model cu actionare prin lichide ER.

Evident, miscarea si orientarea este realizata prin controlul presiunii fluidului, dar ulterior, controlul vāscozitatii asigura o buna stabilitate a miscarii.

13.2.2 Sisteme cu actionare extrinseca

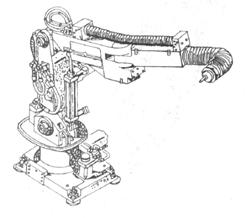
Pentru aceste sisteme sursa motoare se gaseste pozitionata īn afara structurii flexibile a bratului, actionarea fiecarui element si modul realizāndu-se prin diverse modalitati de transmisie. Cel mai cunoscut sistem de transmisie este cel realizat pe baza de cabluri tractate electric sau hidraulic. Īn figura 13.8 este prezentat robotul ACMA la firmei Renault al carui terminal cu functie tentacul-trompa este utilizat īn instalatiile de vopsire automata. Elementele flexibile sunt grupate īn module, fiecare modul fiind activat printr-un sistem de cabluri astfel dispuse īncāt sa asigure o distributie uniforma a fortei de-a lungul bratului. (figura 13.9). Īn cadrul fiecarui modul, elementele flexibile sunt pasive.

Figura 13.8   Robotul ACMA-Renault.

Figura 13.9 Modelul cu tractare pe cabluri

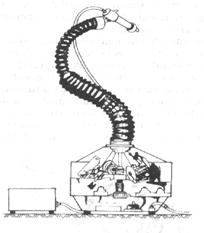
Un robot reprezentativ al acestei familii este robotul HB-Hitachi (figura 13.10) utilizat īn operatii de vopsire si grunduire. Robotul este utilizat din doua tronsoane cu actionare electrica independenta. Fiecare tronson este format dintr-un numar de elemente - vertebre a caror miscare este ghidata de-a lungul unor suporturi elastice printr-o tractare cu cabluri. Vertebrele au o forma specifica astfel īncāt sa permita o mobilitate la cca 150 una fata de cealalta, īn orice directie.

Figura 13.10   Robotul HB-Hitachi.

Īn cadrul laboratorului de Robotica al Universitatii din Craiova a fost realizata familia de roboti TEROB (TEntacle ROBot). Modelul TEROB-01 este un brat cu actionare electrica (13.11) prin cabluri. Sistemul cuprinde trei tronsoane, fiecare tronson fiind format din cinci elemente articulate. Un sistem de cabluri permite actionarea individuala a fiecarui element.

Figura 13.11 Modelul TEROB-01.

Modelul TEROB-02 (figura 13.12) este un robot al carui brat cuprinde opt elemente articulate prin cuple sferice ceea ce asigura o mare mobilitate īntregii structuri mecanice. Comanda robotului se realizeaza prin gruparea elementelor īn doua tronsoane, activarea fiecarui element fiind actionata individual prin cabluri actioanate cu motoare pas cu pas ceea ce faciliteaza procedurile de generare a comenzii si simplifica sistemul de comanda prin eliminarea traductoarelor de reactie.

Figura 13.12 Modelul TEROB-02

Modelul TEROB-03 este un robot cu actionare electrohidraulica format din trei module, fiecare continānd 12 elemente de rotatie cu doua grade de libertate. Actionarea hidraulica este suficient de puternica pentru dezvoltarea unor functii de manipulare cu sarcini de 1,5 daN..

Figura 13.13 Modelul TEROB-03

13.3 Modelul cinematic

Pentru analiza cinematica a acestor sisteme, se va considera un brat tentacul ideal, cu o masa uniform distribuita, cu o flexibilitate ideala īn sensul ca bratul poate lua orice forma īn spatiul 3D (figura 13.14.).

Figura 13.14 Model ideal

Tehnologic, o astfel de structura presupune existenta unei "coloane verte-brale" cu celule periferice care pot determina, printr-o actionare intrinseca sau extrinseca, forma dorita a bratului.

Īn esenta, din punct de vedere cinematic, un model tentacular este definit printr-o curba C care este descrisa parametric printr-un vector si un sistem de referinta asociat definit prin matricea ale carei coloane reprezinta versorii sistemului (figura 13.15). Parametrul independent s reprezinta lungimea arcului de la origine pāna īn punctul curent P. Se va considera ca lungimea totala a bratului pe curba C este l.

Pozitia unui punct s pe curba C este definita prin vectorul de pozitie

(13.1)

unde . Īn cazul unei evolutii dinamice, se va introduce variabila temporala t, .

Parametrizarea curbei C va fi realizata prin doua unghiuri si q(s). Pentru fiecare punct , orientarea robotului este data de un sistem vectorial ortonormat cu originea īn punctul . Pe īntrega structura a curbei C se poate defini o parametrizare sub forma:

(13.2)

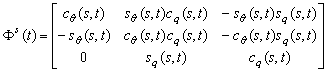(13.3)

unde , , etc.

Pentru o variatie infinit mica ds īn lungul curbei C, noul vector de pozitie va fi:

(13.4)

iar matricea va avea forma:

(13.5)

Vectorul de pozitie poate fi exprimat si prin componentele sale:

unde .

Figura 13.15 Versorii sistemului de referite

Din punct de vedere cinematic, se poate adopta deci urmatoare interpretare [4]: īn orice punct definit de variabila s, relatiile (13.3)- (13.6) determina pozitia curenta, matricea contine orientarea robotului iar forma robotului este determi-nata de functiile si q(s).

Modelul dinamic al bratului ideal

Se va reconsidera un model tentacul idealizat, flexibil, īn care vor fi neglijate frecarile si amortizarile interne. Se vor neglija efectele sectiunii asupra dinamicii bratului.

Īn conformitate cu elementele prezentate īn paragrafele anterioare, pozitia unui punct curent M, la momentul t, aflat la distanta s de originea bratului, va fi descris īn spatiul 3D de un vector pe curba C asociata,

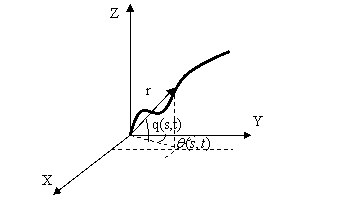
, (13.7)

Figura 13.16

unde:

cei doi parametri unghiulari si q(s,t) determina forma bratului si asigura pozitionarea corespunzatoare a elementului terminal

Analiza dinamica a sistemului impune introducerea elementului de masa dm astfel:

(13.11)

unde va reprezenta densitatea de masa liniara presupusa uniform distribuita pe lungimea bratului.

Se vor utiliza, de asemenea, urmatoarele notatii:

, ,

, ,

, ,

, ,

, ,

, ,

, ,

, ,

unde si vor reprezenta fortele distribuite ce actioneaza īn planurile q si , respectiv si determina evolutia formei bratului.

Corespunzator coordonatelor de pozitie, viteza īn fiecare punct, de-a lungul bratului, va fi definita prin

unde:

Determinarea ecuatiilor de stare care guverneaza miscarea unui brat tentacular este o problema extrem de complicata. Structura continua a modelului, neliniaritatile existente, distributia fortelor si parametrilor pe lungimea bratului fac dificila aplicarea unor metode conventionale. Īn cele ce urmeaza se vor obtine ecuatiile de stare prin utilizarea ecuatiilor lui Lagrange extinse pentru sisteme infinit dimenisionale ceea ce impune calculul energiilor mecanice ale bratului. Pentru un element dm, energia cinetica si potentiala va fi:

(13.15)

(

unde:

Energiile totale ale bratului se vor obtine prin integrarea relatiilor (13.15), (13.17) cu substituirea corespunzatoare a marimilor definite prin expresiile (13.9) si (13.14),

(

Pentru obtinerea modelului matematic se vor substitui aceste expresii īn ecuatiile lui Lagrange adoptate pentru sistemele infinit dimensionale [2, 11]:

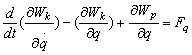
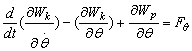
unde , reprezinta derivatele partiale functionale ( īn sens Gateaux) definite ca variatia functionalei W īn raport cu la punctul .

De exemplu, are forma urmatoare:

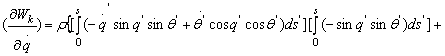
Īn mod similar sunt calculate si celelalte derivate partiale. Substituind aceste rezultate īn ecuatiile lui Lagrange se obtine forma finala a modelului matematic,

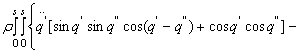
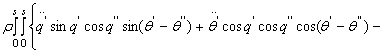
Ecuatiile (13.23), (13.24) pot fi considerate ca ecuatii de stare ale unui brat tentacul ideal. Reamintim ca īn definirea acestui model au fost neglijate frecarile si efectele amortizarilor interne. Chiar si cu aceste simplificari, ecuatiile respective reprezinta un model integro-diferential, puternic neliniar care va ridica probleme deosebite īn abordarea problemelor de conducere.

Īn foarte multe aplicatii, atāt pentru simplificarea tratarii cāt si pentru abordarea unor cazuri specifice, modelul dinamic spatial 3D este īnlocuit cu un model planar 2D, de exemplu pentru un robot ce opereaza īn planul OYZ. Īn acest caz, parametrul principal este reprezentat de unghiul īntre tangenta la curba si axa OY,

(13.25)

Modelul dinamic se va obtine prin particularizarea modelului (13.24)- (13.25) si va avea forma

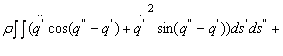
unde F este forta generalizata ce determina modificarea formei, miscarea, bratului īn planul OYZ al variabilei q.

13.5 Sistem de conducere distribuit cu lichide ER

13.5.1 Caracteristici tehnice

Se va considera un model tentacul format prin legarea īn cascada a unor module de forma celor prezentate īn figurile 13.17 a si b. Fiecare modul, element, poate atinge orice orientare īn spatiul 3D.

Constructiv, modulele sunt de tipul intrinsec, īn care miscarea de īncovoiere este obtinuta prin presiunea exercitata de un fluid asupra peretilor terminali. Īn figura 13.18 este reprezentat un astfel de modul format dintr-un cilindru divizat īn trei camere. Peretii cilindrului sunt realizati din cauciuc īn care sunt integrate fibre circulare pentru asigurarea unei rigiditati a īntregii structuri. Prin cresterea presiunii unei camere, cilindrul se va īncovoia īn partea opusa a acesteia. Un control corespunzator al presiunii īn fiecare camera va determina īncovoierea cilindrului īn directia dorita.

Īn afara controlului presiunii, sistemul contine un control suplimentar oferit de proprietatile speciale ale lichidului utilizat. Solutia adoptata la acest model se bazeaza pe utlizarea lichidelor electrorheologice (ER) a caror vāscozitate poate fi controlata printr-un cāmp electric extrem de intens (~). Īn acest scop este introdus un circuit suplimentar de control al potentialului electric format dintr-o retea de electrozi distribuita la periferia cilindrului, retea supusa unui potential uniform distribuit pe lungimea cilindrului (figura 13.19). Īn functie de legea de distributie a potentialului se poate obtine o distributie corespunzatoare a vāscozitatii fluidului.

Figura 13.17   a. - un tentacul ideal 3D

Figura 13.18 Structura unui modul

Figura 13.19 Distributia vāscozitatii in modul

13.5.2 Modelul planar aproximativ

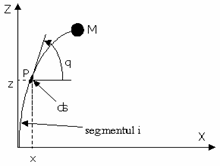
Pentru simplificarea analizei, se va studia modelul tentacul planar (figura 13.20) ce opereaza īn planul OXZ.

Figura 13.20 Modelul planar OXZ

Se vor reconsidera ecuatiile (13.26) ale modelului dinamic planar si se va introduce o discretizare uniforma s₁, s₂, ...s_N a variabilei spatiale s:

(13.27)

, (13.28)

(13.29)

si īn plus, va fi admisa restrictia

, i,j=1,2,...,N (13.30)

unde este o constanta pozitiva suficient de mica.

Din (13.26), cu restrictia (13.30) se obtine modelul discret al bratului sub forma:

(13.31)

unde:

(13.32)

(13.33)

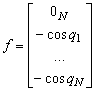(13.34)

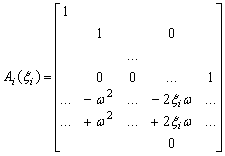(13.35)

O_N si I_N sunt matricea nula si matricea identitate de dimensiunea , respectiv, iar si sunt definite prin

(13.36)

īn care D=2r este diametrul cilindrului, este factorul de amortizare, E este modulul de elasticitate echivalent al materialului compozit.

13.5.3 Sistemul de conducere

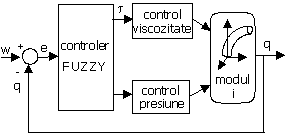
Sistemul de control contine doua subsisteme: un sistem de control conventional de tip electrohidraulic al presiunii fluidului si un sistem de control cu structura variabila bazat pe controlul vāscozitatii fluidului ER (figura 13.21).

Figura 13.21 Sistemul de conducere

Figura 13.22   Evolutia traiectoriilor pe planurile de comutare

Metoda de conducere se bazeaza pe principiul sistemelor cu structura variabila a caror evolutie este descompusa īn doua parti: miscarea pe traiectoria conventionala si miscarea fortata pe o traiectorie īn lungul dreptei de comutare. Īn acest sens, evolutia complexa pe cele 2N grade de libertate este descompusa pe N planuri definite prin parametrii , pentru fiecare plan impunāndu-se o anumita dreapta de comutare (Figura 13.22).

Miscarea este descompusa īn doua parti: īn prima parte se produce controlul "conventional" prin controlul presiunii fluidului (segmentul de traiectorie P₀P₁) iar īn partea a doua, cānd traiectoria penetreaza linia de comutare asociata planului, modificarea factorului de amortizare determina evolutia sistemului pe dreapta de comutare, direct catre origine. Procedura se repeta pentru fiecare plan.

Algoritmul de conducere se bazeaza pe comutarea secventiala a unui sistem cu structura variabila pe diverse submultimi. S₁(e), S₂(e), ..., S_N(e) unde e este eroarea sistemului.

S₁ S₂ S_3... S_N (13.38)

iar evolutia pe o suprafata are loc numai daca se realizeaza, īn prealabil, ecuatiile pe suprafetele predecesoare,

, , ...,

O astfel de strategie īnseamna, de fapt, descompunerea sistemului complex de ordinul 2N īn N subsiteme de ordinul 2, fiecare subsistem evoluānd dupa algoritmul clasic al sistemelor cu structura variabila cu dreapta de comutare.

Justificarea teoretica a unui astfel de sistem distribuit de conducere se obtine plecānd de la modelul dinamic al erorii īn jurul unui punct de functionare.

Se vor considera: w=col(w₁, w₁,...,w_N) - pozitia dorita a bratului, presupusa constanta si x^s, u^s - vectorii regimului stationar pentru stare si control, respectiv, si se va defini eroarea globala sub forma:

(13.40)

unde:

, i=1,2,...,N (13.41)

(13.42)

(13.43)

Modelul dinamic al erorii va fi:

(13.44)

unde:

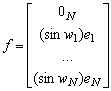(13.45)

Se va nota prin:

(13.46)

iar planurile de comutatie se vor defini prin

(13.47)

unde:

, (13.48)

Īn prima parte a miscarii, controlul evolutiei catre o dreapta de comutare definita prin relatia (13.47) se obtine utilizānd o functie Liapunov de forma:

unde P este o matrice pozitiv definita si simetrica.

Legea de conducere se obtine din ecuatia clasica a metodei a II-a a lui Liapunov [7, 8]:

(13.50)

unde Q este o matrice pozitiv definita iar componenta neliniara are forma (13.45). [14]. Se obtine:

daca (13.51)

daca

unde:

i=1,...,N

Īn momentul īn care traiectoria penetreaza dreapta de comutare S_i(e), sistemul este fortat sa evolueze direct catre origine prin controlul factorului de amortizare global . De exemplu, la comutarea legii de miscare pe prima dreapta S₁(e), evolutia erorii este data de:

(13.53)

si stabilitatea miscarii impune ca:

(13.54)

Din (4.5.9), (4.5.18) se obtine:

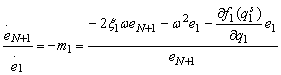
sau:

ceea ce impune ca factorul de amortizare sa verifice relatia:

(13.56)

Conditia (13.56) determina evolutia sistemului fortat, pe dreapta de comutare S₁(e), catre origine:

e₁=0

(13.57)

Dupa atingerea acestor parametrii, se controleza evolutia pe a doua suprafata de comutare:

(13.58)

care devine:

(13.59)

Evolutia fortata catre origine (e₂=0, ) va impune controlul factorului de amortizare dupa o procedura similara, deci:

Algoritmul de conducere va consta deci īntr-o aplicare succesiva a ecuatiilor (13.51) ce determina evolutia catre suprafetele de comutare si ulterior o modificare a factorului de amortizare, pe diferitele segmente ale bratului. Aceasta crestere a coeficientului se va obtine prin cresterea corespunzatoare a cāmpului electric aplicat pe suprafata lichidului ER. O exemplificare a mecanismului de conducere este ilustrata īn figura 13.23.

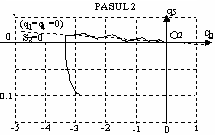
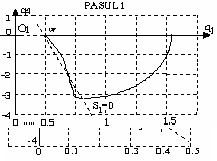
Figura 13.23 Conducerea secventiala distribuita

13.5.4 Control fuzzy

Algoritmul de conducere prezentat mai sus ofera posibilitatea introducerii unor reguli fuzzy si implementarea unui controler specific. Īn acest sens, se vor considera ca marimi de intrare variabilele erorii e_i si iar iesirile controlerului vor fi semnale de activare a presiunii fluidului si a vāscozitatii acestuia. Se va considera un spatiu normalizat atāt pentru marimile de intrare cāt si pentru variabila de iesire asociata presiunii. Pentru controlul vāscozitatii se va pastra iesirea nenormalizata. Pentru implementarea controlerului fuzzy se vor introduce functiile de apartenenta pentru marimile de intrare si de iesire (Figura 13.24).

S-au utilizat etichete lingvistice uzuale care sa identifice asocieri cu valorile crisp ale variabilei respective, de exemplu, NB= NEGATICE BIG (NEGATIV MARE) determina o multime fuzzy corespunzatoare domeniilor negative extreme ale variabilelor de intrare sau iesire, NM= NEGATICE MEDIUM, etc.

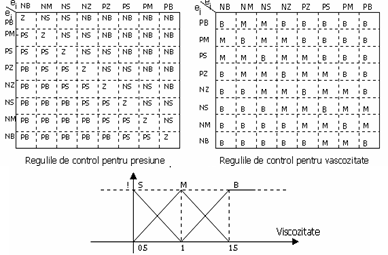
Regulile de control lingvistic se determina pe baza algoritmului discutat īn paragraful precedent. O sinteza a acestora poate fi urmarita īn Tabelul 13.1. pentru controlul presiunii fluidului si pentru controlul vāscozitatii.

Figura 13.24 Functii de apartenenta.

Tabelul 13.1 Regulile de control fuzzy.

Caracteristicile principale pot fi sumarizate astfel:

Valori negative ale presiunii sunt plasate deasupra diagonalei principale iar cele pozitive, dedesubt, conform relatiei (13.52).

Valorile fuzzy ale presiunii cresc odata cu distanta fata de diagonala principala si descresc pentru vāscozitate.

Valorile zero ale presiunii si valorile maxime ale vāscozitatii sunt plasate pe diagonala principala.

13.6 Controlul pozitiei prin legi de conducere

conventionale

Modelul matematic discutat īn paragraful 13.4. arata clar dificultatea stabilirii unei legi de conducere adecvate datorita complexitatii ecuatiilor ce guverneaza miscarea unei structuri hiper-redundante. Ecuatiile integro-diferentiale, cu componente neliniare dificile de tratat, pun probleme deosebite īn determinarea unor solutii corespunzatoare īn conducerea sistemului īn scopul obtinerii unor performante impuse.

Īn paragraful precedent s-au folosit cāteva metode aproximative care au permis o abordare simplificata a conducerii unui brat tentacul, aproximari ce evident se vor repercuta asupra calitatii conducerii sistemului.

Īn cadrul acestui paragraf se vor propune cātiva algoritmi care vor permite implementarea unor controlere de tip conventional PD fara a utiliza modelul matematic complicat al bratului mecanic. Metoda se bazeaza pe utilizarea unor criterii energetice pentru un sistem de conducere al carui criteriu de performanta īl constituie atingerea unei pozitii dorite fixe.

13.6.1 Relatii energetice ale unui model tentacular

Pentru simplificarea tratarii se va studia varianta planara OYZ a modelului tentacul ideal, neglijānd frecarile si eventualele amortizari interne. Pentru acest model, coordonata principala este unghiul īntre tangenta la curba modelului si axa OY:

q=q(s)

sau, īntr-o miscare dinamica, la momentul t:

q=q(s,t)

Figura 13.25 Determinarea relatiilor energetice.

Se va considera ca pozitia initiala a bratului este orizontala, stationara, deci energia cinetica si potentiala va fi zero.

Se va presupune ca lucrul mecanic pentru miscarea a (l-s) din lungime, din pozitia initiala, este L(l-s). Daca un element este deplasat printr-un moment M īntr-o noua pozitie definita printr-un unghi q, la momentul t, noua valoare a lucrului mecanic va fi (Figura 13.25):

(13.63)

unde:

(13.64)

iar:

(13.65)

īn care s-a presupus ca evolutia bratului este determinata printr-o forta F aplicata normal pe curba C a "coloanei vertebrale" a sistemului.

Relatia (13.63) va deveni:

(13.66)

Se poate defini derivata lucrului mecanic:

iar din (13.63) rezulta:

Prin integrare, se obtine:

(13.68)

unde:

iar pentru īntregul brat, de lungime l:

, (13.69)

Rezultatul de mai sus poate fi extins pentru modelul 3-dimensional controlat prin doua forte uniform distribuite , īn planul celor doua coordonate generalizate q(s,t), :

(13.70)

Din formula (13.70), prin aplicarea legii conservarii energiei se obtine:

unde si reprezinta energia cinetica totala si energia potentiala totala la momentul t si 0, respectiv.

Din relatia (13.71) se obtine, de asemenea, o formula utila īn cele ce urmeaza:

13.6.2 Legi de conducere

Pe baza rezultatelor anterioare se va propune un sistem de conducere pentru atingerea unei pozitii dorite fara a utiliza modelul matematic al bratului (figura 13.26).

Controlul pozitiei bratului īnseamna controlul miscarii acestuia pentru a atinge o pozitie dorita definita prin curba:

,

Figura 13.26 Sistemul de conducere pentru atingerea unei pozitii dorite

Eroarea sistemului de conducere se va defini prin:

,

,

a)               Conducerea uniform distribuita PD.

Se propune o lege de conducere de forma:

unde, sunt coeficienti pozitivi.

Sub aceasta forma, relatiile (13.75) reprezinta o lege de conducere clasica de tip PD īn care marimea de conducere generata, fortele si sunt uniform distribuite de-a lungul bratului.

Īn scopul de a aprecia calitatea acestui sistem de conducere, nu se va apela la solutia clasica ce implica modelul dinamic extrem de complicat al bratului ci se va utiliza metoda Liapunov īntr-o constructie speciala [4, 10]. Se va propune urmatoare functia Liapunov.

(13.76)

Evident, V(t) este pozitiv definita īntrucāt termenii care definesc energiile cinetica si potentiala sunt pozitivi sau zero:

Ţinānd cont de relatiile energetice stabilite īn paragraful anterior, derivata functiei (13.76) va avea forma:

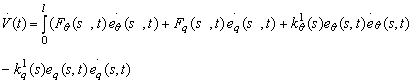
sau, īnlocuind expresiile functiilor de conducere , din (13.75), rezulta:

deci:

ceea ce arata stabilirea sistemului de conducere si evolutia spre zero a erorii.

Pentru ilustrarea acestei metode se vor simula cāteva exemple de conducere utilizānd tehnica SIMULINK din MATLAB.

Exemplu 1. Se considera un manipulator tentacul ce opereaza īn spatiul de operare OXYZ. Parametrii mecanici ai sistemului sunt si lungimea l=0,6m. Se va considera ca pozitia initiala a bratului este cea orizontala (axa OY), definita de:

iar pozitia dorita este reprezentata de o dreapta īn spatiul OXYZ definita prin:

; ;

Legea de conducere este de forma (13.75), unde:

Simularea sistemului de ecuatii integro-diferentiale ale bratului mecanic s-a realizat utilizānd o discretizare a spatiului variabilei s cu un increment :

, i=1,2,...,6

iar ecuatiile diferentiale rezultate s-au simulat īn MATLAB.

Rezultatele simularii sunt sugetiv ilustrate īn figura 13.27, īn care se poate urmari atāt pozitia initiala, cea finala precum si īnca zece pozitii intermediare.

Figura 13.27 Evolutia bratului catre pozitia dorita D

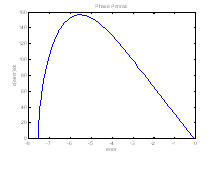
Figura 13.28 Portretul de faza al miscarii.

Pentru o apreciere cantitativa a evolutiei sistemului, īn figura 13.28 s-a reprezentat portretul de faza al miscarii, unde s-a considerat eroarea globala a sistemului de conducere definita prin:

(13.81)

(13.82)

Ca si īn reprezentarea simulata a evolutiei bratului (figura 13.27) se remarca buna evolutie a sistemului, traiectoria de faza evoluānd de la o valoare globala a erorii de cca +7.6 catre dreapta de comutare si de aici catre origine.

Exemplul 2. Un nou test de conducere a fost aplicat aceluiasi brat mecanic, plecānd din aceeasi pozitie initiala, dar pentru care pozitia dorita este reprezentata de o curba:

;

; i=1,2,...,6

Legea de conducere are aceeasi forma cu cea utilizata īn aplicatia precedenta iar coeficientii au valori date de (13.80). Miscarea bratului, simulata īn 3-D, poate fi urmarita īn figura 13.29 precizāndu-se, din nou cāteva pozitii intermediare.

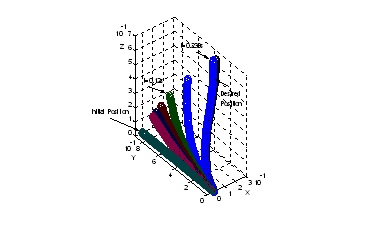
Aspectul calitativ al miscarii este, de asemenea, bine reliefat īn evolutia īn planul fazelor din figura 13.30 unde se poate constata aceeasi convergenta spre origine a erorii si derivatei acesteia.

Figura 13.29 Evolutia bratului catre pozitia dorita C.

Figura 13.30 Portretul de faza al miscarii.

Exemplul 3. O mai buna apreciere a performantelor sistemului de control poate fi obtinuta daca se analizeaza modelele planare. Īn acest sens se va studia miscarea unui brat tentacular ce evolueaza īn planul OXZ. Modelul dinamic este obtinut din modelul spatial, ecuatiile (13.23), (13.24) pentru . De asemenea, legea de conducere va avea forma:

(13.84)

unde coeficientii , sunt alesi la valorile:

Pozitia initiala va fi considerata axa verticala OZ a sistemului:

;

iar pozitia dorita este data sub forma unui semicerc care poate fi aproximat prin:

; i=1,2,...,6

Rezultatele simularii sunt prezentate īn figurile 13.31 si 13.32.

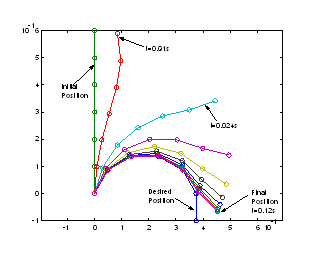
Īn figura 13.31 este prezentata evolutia bratului īn plan precum si cāteva pozitii intermediare iar īn figura 4.32 poate fi urmarit portretul de faza al miscarii.

Figura 13.31 Miscarea bratului īn planul XOZ.

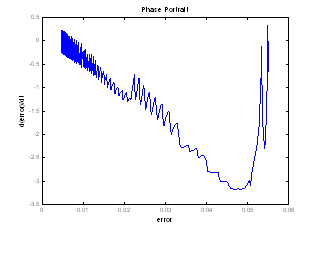
Figura 13.32 Portretul de faza al miscarii.

b.               Conducerea uniform distribuita PD cu ponderare spatiala

Un sistem de conducere mai performant se obtine printr-o lege de conducere sub forma:

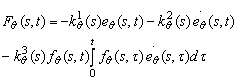(13.87)

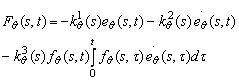(13.88)

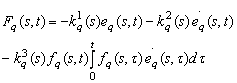(13.89)

unde , , , , , sunt coeficienti pozitivi, iar , reprezinta functii de pondere spatiala.

Al treilea termen al legii de conducere introduce o functie de ponderare pentru facilitatea conducerii īn cazul īn care curba ce defineste pozitia dorita a miscarii nu are o forma "neteda" prezentānd numeroase "colturi" si elemente de discontinuitate.

Stabilitatea miscarii bratului printr-o conducere de forma (13.87), (13.88) este demonstrata tot prin metoda a doua lui Liapunov utilizānd o functie de forma:

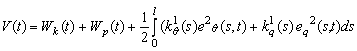
(13.90)

Īn acest caz se va obtine:

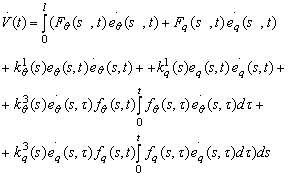
Introducerea legilor de conducere (13.87) si (13.88) īn relatia (13.90) determina o functie sub forma:

deci:

Pentru ilustrare acestei legi de conducere se va simula sistemul pe un exemplu planar.

Exemplu 4. Se considera un brat ce evolueaza īn planul XOZ, plecānd din pozitia initiala, axa verticala OZ iar pozitia dorita este data de forma S definita prin:

;;;

;; ; (

Se propune o lege de control (13.88) la care coeficientii sunt alesi īn forma:

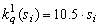
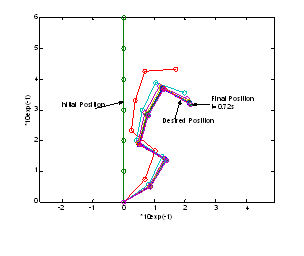
Evolutia bratului poate fi urmarita īn figura 13.33, iar portretul de faza asociat īn figura 13.34.

Figura 13.33 Miscarea bratului pe pozitia dorita S

Figura 13.34 Portretul de faza al miscarii

13.7 Alegerea parametrilor sistemului de conducere

Alegerea anterioara a aratat ca legile de conducere adoptate, fie sub forma (13.75), fie sub forma (13.87), (13.88), determina stabilitatea miscarii fara a lua īn consideratie complexitatea sistemului dinamic. Cu toate acestea, obtinerea unor performante corespunzatoare impune introducerea unor criterii care sa permita alegerea coeficientilor legilor de conducere.

Īn acest caz nu va fi suficienta abordarea sistemului numai sub aspect energetic ci va fi necesara utilizarea modelului matematic infinit dimensional.

Pentru simplificarea tratarii se va analiza modelul planar al unui brat, ecuatia (13.80) pentru care coordonata generalizata este variabila q(s,t). Se vor impune, de asemenea, urmatoarele restrictii:

a.        miscarea sistemului corespunde unor deplasari "mici":

, , ,

unde este o constanta pozitiva suficient de mica.

b.        controlul miscarii este un control secvential spatial, īn sensul ca pozitia dorita a bratului este atinsa treptat, pas cu pas, īncepānd cu primul element (baza) catre elementul final.

c.        O discretizare spatiala , i=1,2,...,N se utilizeaza pentru trans-formarea ecuatiei integrale īn ecuatie diferentiala.

Īn acest caz, īn spatiul erorilor, ecuatiile de miscare devin:

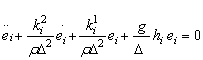, i=1,2,...,N (13.97)

unde:

(13.98)

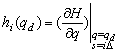(13.99)

iar H=H(q) este determinat de componenta gravitationala:

(13.100)

Ecuatia (13.97) poate fi rescrisa īn termenii clasici ai factorului de amortizare si ai pulsatiei naturale :

unde:

Pentru modelul aproximat (13.100) se propune o conducere de tipul DSMC (Direct Sliding Mode Control) [8], o forma specifica a controlului īn regim alunecator, de-a lungul unei drepte de comutare, prin modificarea factorului de amortizare . Evolutia sistemului este compusa din doua parti: evolutie libera spre dreapta de comutare si o evolutie fortata pe dreapta de comutare.

Figura 13.35 Controlul DSMC

Se va presupune ca dreapta de comutare este definita de relatia:

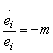(13.103)

Iar conditiile de miscare pe dreapta vor fi [4, 8]:

(13.104)

si

(13.105)

De exemplu, pentru miscarea simulata din Exemplu 3, daca se alege o pulsatie naturala , i=1,2,...,6 atunci conditiile (13.104) si (13.105) vor fi verificate pentru:

, i=1,2,...,6

ceea ce va determina o alegere a coeficientilor:

, i=1,2,...,6

Utilizarea acestor coeficienti a permis obtinerea miscarii simultate din figurile 13.31 si 13.32.

Daca pozitia dorita a bratului are forme mai dificil de controlat (de exemplu - forma S din 13.33) se impune introducerea unor functii de penalizare. O alegere posibila a acestor functii ar fi cea legata de penalizarea distantei īntre pozitiile sistemului si cele dorite īn punctele critice ale miscarii, de exemplu:

, i=1,2,...,6 (13.106)

Implemenatarea acestei legi a determinat evolutia prezentata īn figurile 13.33 si 13.34.

13.8 Conducere fuzzy

Sistemul de conducere dezvoltat īn paragrafele anterioare permite introducerea metodelor fuzzy īn implementarea controlerelor. Se vor analiza separat doua cazuri, cānd pozitia dorita este stationara si cazul īn care pozitia dorita este variabila īn timp.

a.        Pozitia dorita stationara.

Se va considera ca fortele distribuite , sunt generate de un controler fuzzy:

(13.107)

(13.108)

Utilizānd aceeasi functie Liapunov ca si īn paragraful (4.7) se obtine:

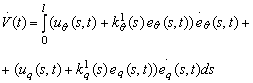
O conditie suficienta de stabilitate poate fi dedusa sub forma:

Daca se introduce o discretizare spatiala , i=0,1,...,N, inegalitatile de mai sus devin:

unde ,...,,..., ,...,

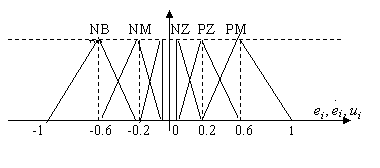
Conditiile (13.112) si (13.117) pot reprezenta suportul pentru definirea unei baze de reguli ale unui controler fuzzy. Īn acest sens, se vor considera functiile de apartenenta din figura 13.36 definite pe un spatiu normalizat al variabilelor ,, , unde NB, NM, NZ, PZ, PM, PB, reprezinta multimile fuzzy NEGATIVE BIG, NEGATIVE MEDIUM, NEGATIVE ZERO, POSITIVE ZERO, POZITIVE MEDIUM, POSITIVE BIG, respectiv.

Figura 13.36 Functii de apartenenta

Tabelul 13.2 Baza de reguli

Baza completa de reguli este reprezentata īn tabelul din Tabelul 13.2, regulile fiind astfel selectate īncāt conditiile de stabilitate (13.110) si (13.111) sa fie respectate.

b.               Pozitia dorita variabila īn timp.

Īn acest caz, se va considera ca legile de conducere ale bratului sunt definite sub forma:

(13.114)

(13.115)

unde si sunt generate de controlere fuzzy. Din aceeasi conditie de stabilitate Liapunov (4.8.3) obtinem:

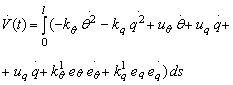
Functia (13.116) este negativ definita daca urmatoarele inegalitati vor fi satisfacute:

Pentru obtinerea regulilor fuzzy pentru cele doua marimi , se va adopta un sistem fuzzy ierarhic cu doua nivele de ierarhizare (figura 13.37). Nivelul 1 are ca variabile de intrare pe , si , , respectiv si genereaza o functie neliniara , , care vor constitui intrari īn al doilea nivel ierarhic īmpreuna cu vitezele de miscare , , respectiv.

Īntr-o scriere generala, marimile , pot fi puse sub forma:

(13.119)

(13.120)

Se va introduce discretizare spatiala utilizata si īn cazurile anterioare:

, i=0,1,2,...,N

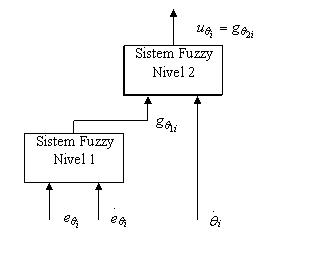
Pentru simplificarea tratarii si micsorarea efortului de calcul pe domeniile variabilelor sunt utilizate numai multimile fuzzy de apartenenta ilustrare īn fF 20l 4eguli.tenenta.ate din Figura 13.38. Cele doua nivele ierarhice vor impune implementarea a cāte 16 reguli pe fiecare nivel, pentru generarea controlerului (Tabelul 13.3).

Figura 13.37 Controlerul fuzzy cu doua nivele

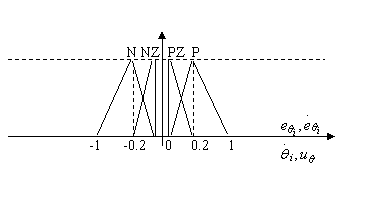
Figura 13.38 Functii de apartenenta pe fiecare nivel

Tabelul 13.3 Baza de reguli pentru sistemul cu 2 nivele

Pentru ilustrarea procedurilor dezvoltate mai sus se va considera problema conducerii bratului spre o pozitie dorita definita de:

; ,i=0,1,2,...,6 (13.121)

si se va implementa un controler fuzzy de forma (13.108) prin baza de reguli prezentate īn figurile 13.36 si 13.37.

Evolutia bratului robotului poate fi urmarita īn figura 13.39 iar portretul de faza al miscarii este prezentat īn figura 13.40. Se remarca aceeasi buna calitate a miscarii si convergenta spre zero a erorii de pozitie.

Figura 13.39   Evolutia bratului prin controlerul fuzzy

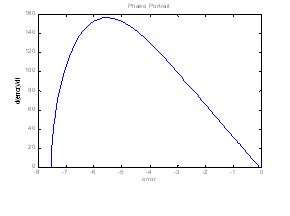
Figura 13.40   Portretul de faza al miscarii

13.9 O problema de interceptie

Īn paragrafele anterioare a fost analizata problematica conducerii unui brat tentacular pentru atingerea unei pozitii fixe sau variabile impuse. O problema speciala este cea definita formal ca o problema de "interceptie a unei tinte". Un exemplu tipic al acestei probleme este cel oferit de lumea vie, prinderea unei pasari de un sarpe (figura 13.41). sarpele urmareste pasarea, estimeaza traiectoria de miscare a acesteia si ataca prada interceptānd-o īntr-o anumita pozitie a miscarii.

Īntr-o transpunere tehnologica, problema de mai sus poate fi reformulata astfel: un brat hiper-redundant tentacular se gaseste īntr-o pozitie initiala (figura 13.42 a) pe axa OZ. O tinta executa o miscare proprie pe o traiectorie necunoscuta. Un estimator al miscarii analizeaza parametrii tintei pe baza carora un sistem de conducere dirijeaza bratul pentru interceptare.

Figura 13.41 Interceptie īn lumea vie.

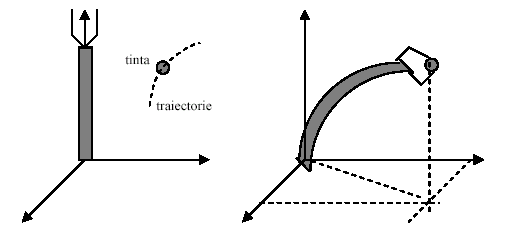
Figura 13.42   Interceptia unui sistem mecanic

O problema de interceptie este o problema de conducere complexa īn care un rol important īl joaca sistemul de estimare, de evaluare, al parametrilor tintei. Se va presupune ca exista un sistem senzorial pentru masurarea parametrilor de miscare ceea ce permite identificarea unui model matematic al tintei.

Pentru simplificarea problemei tratarii se va studia problema de interceptie īntr-un caz planar, miscarile bratului si tintei avānd loc īn planul XOZ.

Modelul dinamic al bratului este dat īn (13.26) care, dupa discretizare , i=0,1,2,...,N si īn conditiile (13.30) poate fi rescris [6, 13] sub forma:

(13.122)

unde M, C sunt matrici (NN), D este un vector neliniar (N1):

(13.123)

iar componentele matricei C depind de compozitia interna a bratului, de exemplu, daca se utilizeaza lichide electrorheologice atunci:

(13.124)

(13.125)

(13.126)

unde definesc parametrii structurii tehnologice [8], si sunt factorul

de amortizare echivalent si respectiv pulsatia naturala a sistemului iar E este cāmpul electric aplicat pentru controlul vāscozitatii fluidului.

Īn cele ce urmeaza, vor fi studiate doua cazuri, cānd parametrii tintei sunt cunoscuti si cānd acestia sunt necunoscuti si urmeaza sa fie identificati.

a.        Parametrii dinamici ai tintei sunt cunoscuti.

Se va considera:

(13.127)

vectorul ce defineste coordonatele pe traiectorie ale tintei īn planul XOZ iar parametrii miscarii vor fi dati de derivata de ordinul īntāi si doi ale acestui vector, determinānd viteza iar , acceleratia tintei.

Īn principiu determinarea parametrilor bratului manipulatorului īntr-o pozitie de interceptie a tintei revine la rezolvarea unei ecuatii diferentiale neliniare de forma:

(13.128)

unde J(q) reprezinta matricea Jacobian a bratului. Relatia de mai sus constituie solutia clasica pentru o problema inversa īn cazul īn care Jacobianul sistemul este nesigular.

Pentru conducerea bratului catre tinta se impune definirea unei erori īntre valoarea dorita, obtinuta prin rezolvarea ecuatiei (13.128), si parametrii reali de miscare ai bratului tentacular:

(13.129)

Se introduce, de asemenea, o eroare generalizata:

(13.130)

unde:

(13.131)

cu alese numere īntregi si pozitive. Este evident ca īn planul erorilor (e,), expresia (13.130) defineste o dreapta.

Introducerea variabilei s permite definirea problemei de interceptie sub forma urmatoare: "tinta" cu parametrii de pozitie (13.127) se considera interceptata daca:

(13.132)

Īn scopul rezolvarii problemei se propune un sistem de conducere definit prin:

(13.133)

unde K este o matrice constanta (NN) iar u este un vector suplimentar de conducere. Pentru determinarea conditiilor impuse matricilor K si vectorului u se rescrie modelul dinamic al bratului (13.122):

(13.134)

care, dupa cāteva transformari, devine:

(13.135)

unde este un vector neliniar (N1) definit pe parametrii miscarii bratului si tintei.

Pentru satisfacerea conditiei (13.132) se va considera o functie Liapunov de forma:

(13.136)

unde P este o matrice pozitiv definita si simetrica. Urmānd procedura clasica a metodei a II-a a lui Liapunov se obtine:

(13.137)

sau, tinānd cont de (13.135):

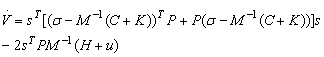(13.138)

Daca se alege K astfel īncāt sa fie o matrice stabila, atunci se va putea īntotdeauna gasi o matrice Q pozitiv definita astfel īncāt:

ultimul termen al expresiei (13.138) este determinat de vectorul de conducere u.

Daca se introduce conditia:

atunci din relatia (13.138) se obtine:

(13.141)

unde este cea mai mica valoare proprie a matricei Q.

Rezumānd rezultatele de mai sus, problema de interceptie se reduce la introducerea unei legi de conducere sub forma (13.133) īn care matricea K sa asigure stabilitatea matricei compuse:

iar componenta u sa verifice o relatie de forma (13.140). Forma particulara a conditiei (13.140) sugereaza introducerea unui controler fuzzy pentru generarea vectorului u.

Algoritmul fuzzy va considera pe s_i si H_i ca variabile de intrare iar u_i este iesirea (fuzzy). Functiile de apartenenta asociate, definite pe spatiile nenormalizate si , respectiv, sunt reprezentate īn figura 13.43. Conditia (13.140) permite implementarea bazei de reguli din Tabelul 13.4.

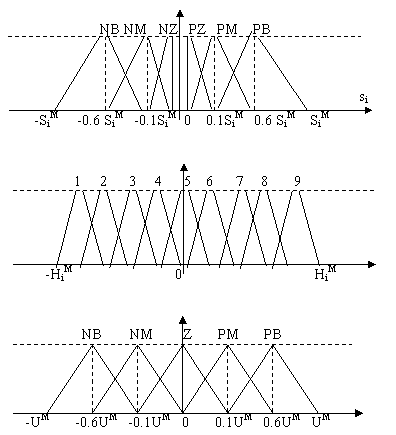
Figura 13.43 Functii de apartenenta

Tabelul 13.4 Baza de reguli a controlerului fuzzy.

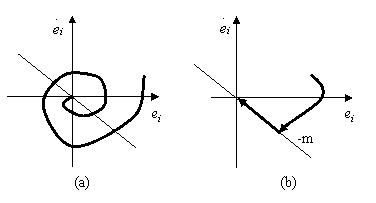
Regulile bazei asigura o miscare stabila īn sensul dat de (13.130), evolutia īn planul erorilor (e,) putānd fi una de tipul celei prezentate īn figura 13.44a. De fapt, miscarea de acest fel corespunde unui proces de interceptie de tipul unei oscilatii amortizate care īn foarte multe cazuri sa nu corespunda unor cerinte de calitate. O procedura de interceptie calitativ superioara poate fi obtinuta pentru o evolutie de tipul celei descrise īn figura 13.44b. Aceasta corespunde metodei DSMC (Direct Sliding Mode Control) descrisa īn paragraful 13.6. Miscarea de interceptie este fragmentata īn doua parti, una prin control fuzzy conventional; variabila u, iar a doua, dupa atingerea dreptei de comutare, direct catre origine, de-a lungul dreptei, prin modificarea factorului de amortizare echivalent, deci a vāscozitatii fluidului.

Figura 13.44   a - miscarea de interceptie conventionala

b - miscarea de interceptie DSMC.

b.               Parametrii dinamici ai tintei sunt partial necunoscuti.

Se va studia, īn continuare cazul īn care parametrii dinamici sunt cunoscuti numai partial, de obicei sistemul de conducere contine un senzor ultrasonic sau infrarosu care permite detectarea pozitiei tintei. Pentru identificarea celorlalti parametrii, viteza si acceleratia se utilizeaza un observer al miscarii. Spre deosebire de metodele clasice abordate īn literatura, se va considera acum cazul īn care masurarea pozitiei va fi obtinuta ca o multime fuzzy iar observerul introdus va genera marimile de iesire, de exemplu viteza ca o marime crisp.

Se va considera ca tinta este definita printr-un model de tipul Takagi-Sugeno iar dinamica miscarii este descrisa prin reguli IF-THEN de forma:

Regula i

IF este F_1i AND ... AND este F_1p

THEN 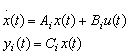(13.143)

unde F_ij (i=1,2,...,r;j=1,2,...,p) sunt multimi fuzzy, x(t), u(t), y_i(t) iar ,..., sunt variabilele masurabile ale sistemului.

Starea finala a sistemului fuzzy este reprezentata de ecuatiile [11]:

unde:

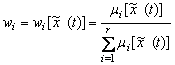(13.147)

iar reprezinta gradul lui īn fuctia de apartenenta a lui .

Este evident ca vor fi satisfacute conditiile:

(

pentru orice t

Pentru estimarea parametrilor se va considera un observer definit de ecuatia [13]:

unde

, ,

,

Modelul definit de relatia (13.150) va reprezenta un observer al sistemului (13.144), (13.145) daca eroarea:

(13.151)

verifica conditia:

(13.152)

Conditia de stabilitate de mai sus poate fi reformulata īn modul urmator:

sau īn raport cu eroare e

Daca se alege un functie Liapunov:

(13.155)

unde P este o matrice pozitiv definita si simetrica, , se obtine:

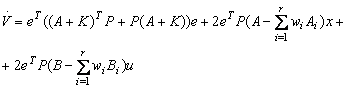(13.156)

Daca se aleg matricile A, B astfel īncāt:

si daca matricea K este astfel aleasa īncāt matricea (A+K) sa fie stabila, atunci, din relatia (13.156) obtinem:

(13.158)

unde este valoare minima a matricei Q, solutie a ecuatiei:

Satisfacerea conditiilor (13.157) precum si alegerea unei matrici K astfel īncāt matricea (A+K) sa fie stabila da posibilitatea evaluarii parametrilor miscarii prin vectorul z. Cunoasterea acestor parametrii permite ulterior introducerea metodelor de interceptie dezvoltate la sectiunea precedenta. Pentru ilustrarea problemei de interceptie se va considera, pentru īnceput cazul īn care parametrii tintei sunt cunoscuti si un algoritm fuzzy de interceptie de tipul celui discutat la sectiunea a) este implementat.

Se considera bratul robotului aflat initial īn pozitie verticala (axa OZ - figura 13.45) iar tinta, īn planul XOZ este definita prin urmatorii parametrii:

Se va considera un spatiu nenormalizat pentru variabilele s, H, u:

Figura 13.45   Interceptie īn plan XOZ

Baza de reguli se obtine prin particularizarea bazei de reguli din Tabelul 13.4 iar functiile de apartenenta au forma prezentata īn figura 13.43. Rezultatele simularii sunt prezentate īn figurile 13.46 si 13.47. Īn figura 13.46 se pot urmarii traiectoriile tintei si ale bratului (punctul terminal), iar īn figura 13.47 este prezentat portretul de faza al miscarii. S-a realizat o interceptie rapida printr-o evolutie pe dreapta de comutare iar convergenta catre zero a erorii indica calitatea ridicata a procesului de interceptie.

Figura 13.46   Traiectorii īn procesul de interceptie

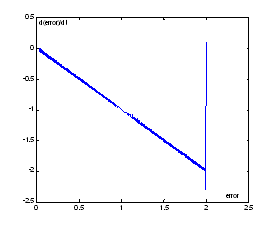
Figura 13.47 Potretul de faza al interceptiei

Īn continuare se va studia cazul īn care sistemul este prevazut numai cu un senzor pentru masurarea pozitiei iar un observer este utilizat pentru identificarea celorlalti parametrii.

Se va considera ca tinta este definita printr-un model dinamic de ordin doi (ecuatiile 13.143) unde A_i, B_i, C_i au forma:

; (13.161)

;

Multimile fuzzy F_1i, F_2i sunt prezentate īn figura 13.48 īn care s-a considerat ca:

;

Parametrii a_1i, a_2i, b_i sunt determinati ca marimi de iesire ale unei proceduri de inferenta cu functiile de aparetenenta prezentate īn Figura 13.49.

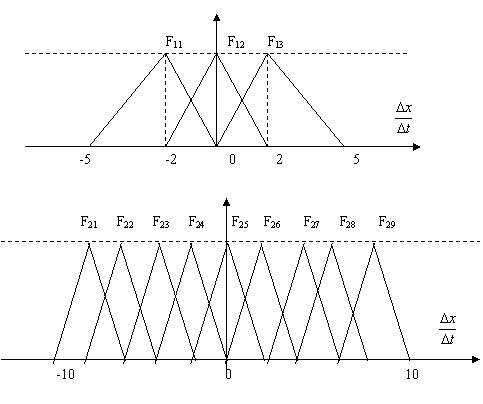
Figura 13.48 Functiile de apartenenta pentru F_1i, F_2i.

Figura 13.49   Functiile de apartenenta pentru a_1i, a_2i, b_i

Se propune un model pentru observerul sistemului de forma (13.150) unde A, B sunt selectati conform conditiei de stabilitate a matricei (A+K):

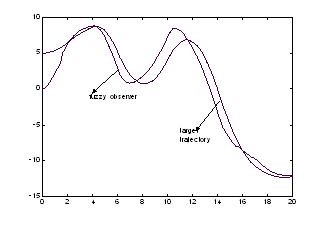
Rezultatele procedurii sunt prezentate īn figurile 13.50 si 13.51, prima ilustrānd evolutia īn spatiu a tintei si a traiectoriei "estimate" prin identificarea parametrilor iar īn a doua figura este prezentat portretul de faza asociat. Cu toata apartenenta "haotica" a traiectoriei se remarca convergenta spre zero a erorii procesului de interceptie.

Figura 13.50 Traiectoriile de interceptie

Figura 13.51   Portretul de faza

13.10 Sisteme de conducere cooperativa

Sectiunile precedente ale acestui capitol au pus īn evidenta complexitatea sistemelor implicate īn conducerea unei structuri hiper-redundante pentru probleme de control care implica miscarea unui singur tentacul īn conditiile īn care obiectul conducerii este formulat īntr-o pozitie finala dorita, fie printr-o interceptie a unei tinte stationare sau mobile.

O problema cu specific deosebit se obtine īn cazul īn care se pune problema cooperarii a doi sau mai multi roboti īn scopul realizarii unei actiuni comune.

13.10.1 Formularea problemei

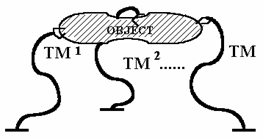
Se va considera sistemul multi-brat tentacular din figura 13.52. Sistemul cuprinde K structuri hiper-redundante fixate pe aceeasi baza ce efectueaza o sarcina impusa, deplasarea īn comun a unui obiect pe o traiectorie dorita. Este evident ca, pe lānga problemele complexe ale controlului miscarii fiecarui brat, apar īn plus si cele legate de conducerea cooperanta a acestora astfel īncāt īn punctele terminale sa fie exercitata o anumita forta ce va putea asigura miscarea impusa a obiectului-sarcina.

Figura 13.52 Sistemul multi-cooperativ

Studiul acestor probleme va fi tratat, īn primul rānd, pe un sistem cooperativ planar format din doua brate ce opereaza īn planul XOZ (figura 13.53).

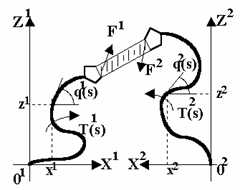
Figura 13.53   Sistemul cooperativ planar

Modelul dinamic al sistemului este derivat din ecuatiile dinamice ale bratului, prezentate īn paragrafele precedente, la care se adauga termenii determinati de forta de contact īntre terminalul bratului si robot [12]:

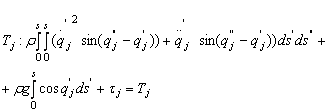(13.163)

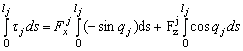, j=1,2,... (13.164)

unde notatiile sunt aceleasi cu cele prezentate īn prima parte a capitolului, variabila spatiala s este definita pe lungimea fiecarui brat:

, j=1,2,...

coordonatele si fortele generalizate sunt:

, ,

, , , j=1,2,...

iar este forta distribuita īn jurul bratului ce determina forta F^j īn punctul terminal al bratului. Relatiile īntre si F^j sunt stabilite de ecuatia (13.164) si sunt determinate de principiul de conservare al energiei mecanice. Se neglijeaza frecarile īn punctele terminale, fata de obiect, si nu sunt luate īn calcul energiile determinate de elasticitatea componentelor. Toate aceste marimi sunt exprimate īn sistemele de coordonate asociate fiecarui brat.

13.10.2 Sistemul de conducere

Strategia de control este o strategie pe doua nivele ierarhice, un nivel superior care asigura controlul cooperarii bratelor īn scopul efectuarii miscarii dorite, pe traiectorie, a obiectului-sarcina, si un nivel inferior care determina miscarea individuala a fiecarui brat.

Īn cadrul nivelului superior, obiectivul sistemului este sa asigure evolutia pe traiectorie a sarcinei prin forta generala aplicata acesteia:

(13.165)

unde F⁰ este forta rezultanta exprimata īn sistemul de referinta absolut, F_j sunt fortele exercitate īn terminalul fiecarui brat, iar este o matrice de transformare din sistemul de coordonate al bratului j īn cel absolut. Dinamica miscarii sarcinei, pe traiectorie, este data de o relatie de forma:

(13.166)

unde M este masa obiectului, iar r defineste vectorul de coordonate al acestuia:

(13.167)

r=r(t) desemnānd ecuatia traiectoriei obiectului. Conditiile pentru determinarea fortelor F_j din ecuatiile (13.165), (13.166) se completeaza cu restrictiile impuse sub

forma:

(13.168)

Aceste inegalitati sunt impuse de frecarile sistemului, limitarile energetice ale fortelor aplicate, etc. Īn unele cazuri, calculul fortelor F_j se completeaza cu o problema de optimizare:

unde este indicele de optim impus de obicei dupa criterii de energie minima. Relatiile (13.165), (13.166), (13.168), (13.169) formeaza suportul de calcul pentru determinarea fortelor de contact īntre punctele terminale ale bratelor si obiect.

Pentru implementarea strategiei de control la al doilea nivel ierarhic, inferior, se va utiliza modelul aproximat al unui brat tentacular, folosind aceeasi tehnica ca cea dezvoltata īn sectiunile 13.5, 13.6:

, j=1,2,... (13.170)

unde indicele j desemneaza bratul si se ataseaza tuturor variabilelor asociate:

(13.171)

iar M_j, C_j, D_j, sunt matrici (nn), (nn), (n2) respectiv.

Īn general fortele de contact sunt de evaluat exact, asupra lor impunāndu-se, de obicei, o restrictie de forma:

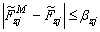(13.172)

unde , sunt constante pozitive, iar , definesc valorile maxime estimate ale acestor forte.

Problema conducerii, la acest nivel ierarhic, consta īn determinarea fortelor F_j astfel ca traiectoria reala a sistemului global (obiect plus brate) sa convearga catre traiectoria dorita. Pentru rezolvarea acestei probleme se va considera sistemul din figura 13.54 īn care q_dj, F_dj desemneaza valorile dorite ale pozitiei si fortei, respectiv iar q_j, F_j, valorile reale masurate.

Eroarea, pe traiectorie, va fi:

(13.173)

unde a fost eliminat indicele j, pentru simplificarea scrierii.

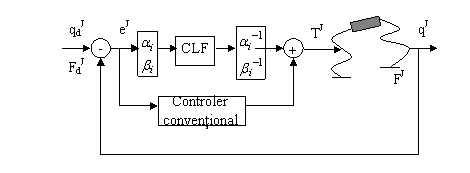
Sistemul de conducere cuprinde doua parti: un controler conventional care implementeaza o strategie clasica de conducere si un controler fuzzy conectat īn paralel cu primul.

Figura 13.54 Sistemul de conducere

Īn concordanta cu aceasta structura, legea de conducere va avea forma:

unde s desemneza variabila īn planul fazelor:

(13.176)

,

K este o matrice (nn), H reprezinta componentele neliniare definite de-a lungul valorilor dorite, iar u_F este componenta de control generata de controlerul fuzzy.

Pentru a gasi conditiile impuse componentelor sistemului de conducere se analizeaza ecuatia (13.170) de-a lungul traiectoriei dorite:

(13.178)

care poate fi rescrisa sub forma:

(13.179)

sau

(13.180)

Pentru a gasi conditiile de stabilitate ale miscarii se va considera o functie Liapunov de forma:

(13.181)

Aplicānd procedura obisnuita utilizata īn aceasta metoda se obtine:

(13.182)

Daca se introduce legea de conducere (13.175) rezulta:

Presupunānd ca urmatoarele conditii sunt īndeplinite:

pozitiv definita (13.184)

, i=1,2,3,... (13.185)

(13.186)

Relatia (13.182) determina ca:

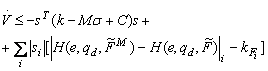
sau:

unde este valoarea proprie minima a lui .

Conditia (13.184) impune matricea de conducere K a buclei conventionale iar relatiile (13.185) si (13.186) permit introducerea unui controler fuzzy. Forma particulara a lui (13.185) sugereaza un controler derivat dintr-un controler cu structura variabila la care iesirea creste proportional cu distanta fata de o dreapta de comutare de forma (13.176).

Se va considera un spatiu normalizat:

(13.188)

unde

reprezentānd factorii de scala corespunzatori.

Baza de reguli este data īn tabelul din Tabelul 13.5 iar functiile de apartenenta utilizate sunt prezentate īn figura 13.55, etichetele lor avānd simbolurile conventionale.

Tabelul 13.5   Baza de reguli

Figura 13.55 Functii de apartenenta

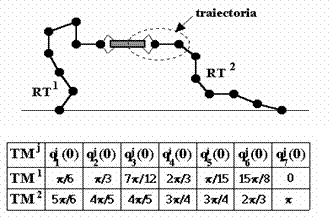
Pentru exemplificare se va considera cazul a doi manipulatori planari ce deplaseaza pe o traiectorie impusa un corp. Fiecare manipulator este format din 7 elemente de lungime . Obiectul, sarcina miscarii, are masa m=1kg si lungime l=0.2m. Pozitia initiala a manipulatoarelor este data īn Figura 13.56.

Figura 13.56 Miscare cooperativa planara - exemplu

Traiectoria dorita este impusa sub forma unei elipse:

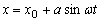
unde x₀ =0.2m, z₀ =0.1m, a =0.3, b =0.1, rad/sec. Se remarca faptul ca traiectoria apartine anvelopei de lucru a celor doua manipulatoare si nu contine singularitati.

Resctrictiile asupra fortei sunt:

N

N

iar incertitudinile asupra masei sarcinii sunt date sub forma:

kg

Pentru calculul fortei īn punctul de contact se utilizeaza un criteriu de forma patratica:

min; min

Figura 13.57 Evolutia factorului k

Figura 13.58   Portretul de faza

Figura 13.59   Evolutia pe traiectorie

Traiectoria dorita se obtine prin rezolvarea ecuatiei [24],

(13.191)

unde w=(x,y)^T iar J(q) este matricea Jacobian a bratului. Evolutia parametrului k īn controlerul conventional este prezentat īn figura 13.57 iar portretul de faza al miscarii si evolutia pe traiectorie sunt prezentate īn figurile 13.58 si 13.59, respectiv.