MECANICA CLASICÃ - FORMALISMUL LAGRANGEIAN

MECANICA CLASICÃ - FORMALISMUL LAGRANGEIAN

Spatiul configuratiilor

Spatiul mecanicii clasice este euclidian si tridimensional. El reprezinta un cadru care contine materia fara a interactiona cu ea. Timpul este unidimensional, absolut si fara nici o legatura cu ceva extern. Pozitia unui punct material in spatiu este specificata cu ajutorul razei vectoare ale carei componente sunt coordonatele carteziene x, y, z. Derivata la timp a razei vectoare este vectorul viteza: , iar derivata la timp a vitezei se numeste acceleratie: . Pentru a specifica pozitia unui sistem de n puncte materiale sunt necesare n raze vectoare sau 3n coordonate.

Definitie Numarul de parametri independenti necesari pentru cunoasterea univoca a pozitiei unui sistem mecanic este numit numarul gradelor de libertate ale sistemului.

In cazul descris acest numar este 3n. In general parametrii independenti care specifica pozitia sistemului nu sunt neaparat coordonatele carteziene ale punctelor materiale, ci orice alte distante si unghiuri (de exemplu: coordonatele specifice sau coordonatele cilindrice , etc.). In multe situatii sistemul mecanic sufera interactiuni cu caracter de legatura adica de limitare impusa pozitiilor reciproce ale corpurilor. Legaturile sunt produse cu ajutorul unor elemente fizice ca: firele, articulatiile, tijele, etc. In cazul in care se pot neglija frecarile (care ne scot din cadrul mecanicii) si masele elementelor de legatura, rolul lor se reduce la o micsorare a num& 424f53e atilde;rului gradelor de libertate ale sistemului mecanic.

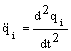Definitie. Cele s marimi oarecare care specifica pozitia unui sistem mecanic (cu s grade de libertate) se numesc coordonatele generalizate ale sistemului mecanic. Derivatele la timp se numesc viteze generalizate iar derivatele acestora se numesc acceleratii generalizate. Experienta, sintetizata in principiul determinismului lui Newton, arata ca starea initiala a unui sistem mecanic (ansamblul pozitiilor si vitezelor punctelor sistemului la un moment dat) determina univoc intreaga

miscare, in sensul de a putea prevedea pozitia sistemului la un moment ulterior. Din punct de vedere matematic aceasta inseamna ca acceleratia la un moment dat este determinata univoc de cunoasterea coordonatelor si vitezelor generalizate la acel moment:

Aceasta ecuatie, postulata de Newton a fost pusa la baza mecanicii clasice . Ecuatiile care leaga acceleratiile de viteze si de coordonate se numesc ecuatii de miscare. Ele sunt ecuatii diferentiale de ordinul al doilea. Integrarea lor permite aflarea functiilor q(t) (numite traiectoriile miscarii sistemului mecanic). Cele 2s constante de integrare necesita cunoasterea coordonatelor si vitezelor generalizate la un moment dat.

Definitie Numim spatiul configuratiilor (spatiul lui Lagrange) un spatiu reprezentativ s - dimensional ale carui axe sunt coordonatele generalizate . Un punct reprezentativ in spatiul configuratiilor corespunde unei pozitii a sistemului mecanic in spatiul tridimensional la un moment dat. Miscarea sistemului mecanic determina punctul reprezentativ sa descrie o curba numita traiectorie in spatiul configuratiilor.

Principiul minimei actiuni (Hamilton)

Problema fundamentala a mecanicii se pune astfel: cunoscand starea unui

sistem fizic la un moment dat t₁, altfel spus cunoscand coordonatele si vitezele generalizate ale sistemului la acest moment si dandu-se fortele care actioneaza asupra sistemului, sa se afle evolutia ulterioara, sau traiectoria urmata de punctul reprezentativ.

numita functia lui Lagrange (sau lagrangeianul sistemului mecanic). Daca la momentele t₁ si t₂ sistemul ocupa pozitii determinate: si , intre aceste pozitii sistemul se misca astfel incat integrala:

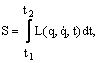
numita actiune, ia o valoare minima.

Observatii:

a.       Aceasta formulare a principiului este valabila doar pentru fiecare parte suficient de mica a traiectoriei. Pentru intreaga traiectorie integrala actiunii trebuie sa aiba un extrem nu neaparat un minim. De aceea principiul se mai numeste "al actiunii extreme"

b.      In spatiul configuratiilor am reprezentat cu linie plina traiectoria reala a sistemului mecanic iar cu linii punctate am reprezentat traiectoriile virtuale. Daca se calculeaza actiunea pe traiectoria reala se obtine valoarea extrema in comparatie cu valorile ei pe traiectoriile virtuale.

c.       Nu intamplator exista si in optica un principiu asemanator: principiul lui Fermat. Acesta afirma ca "drumul efectiv urmat de o radiatie luminoasa printr-un mediu fizic transparent este o extremala a drumului optic:

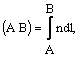
unde n este indicele de refractie al mediului iar dl este elementul spatial.

Fie un sistem mecanic cu un singur grad de libertate (s=1) si 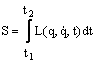actiunea extrema pe traiectoria reala, descrisa de functia q(t).

Consideram o traiectorie virtuala apropiata de cea reala, descrisa de functia: unde este o marime arbitrara constanta foarte mica iar este o functie continua si cu derivata continua, aleasa arbitrar, care satisface conditiile la capete:

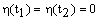
astfel incat cele doua traiectorii, reala q(t) si virtuala sa coincida la capete.

Actiunea pe traiectoria virtuala devine o functie de parametrul :

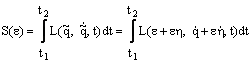
Pentru ca pe traiectoria reala aceasta integrala sa aiba un extremum trebuie satisfacuta conditia:.

Dezvoltam in serie Taylor , neglijand termenii de ordin superior ce contin .

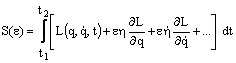
Punem conditia de extremum pentru integrala, derivand in raport cu :

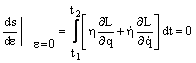
Calculam integrala:

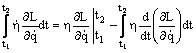
Inlocuind si tinand cont de conditiile la capete vom obtine:

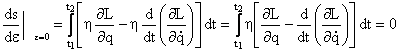
Deoarece este o functie arbitrara ( in acord cu teorema Du Bois-Raymond sau teorema fundamentala a calculului variational), conditia de anulare a integralei implica:

numita ecuatia lui Lagrange.

In cazul unui sistem cu mai multe grade de libertate , trecerea de la traiectoria reala , la cea virtuala , implica dependenta actiunii de s parametri .

iar conditia de extremum 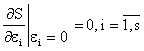, determina obtinerea in mod analog a ecuatiilor Euler-Lagrange :

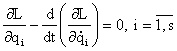
Aceste ecuatii contin toata informatia despre evolutia sistemului intre

momentele t₁ si t_t . Prin integrarea lor se obtin cele s functii q_i(t) - ecuatiile traiectoriei. Precizarea celor 2s conmstante de integrare se face prin cunoasterea coordonatelor si vitezelor generalizate la un moment dat.

Analizand forma ecuatiilor Euler-Lagrange putem deduce cateva proprietati pe care trebuie sa le aiba functia Lagrange:

Daca inmultim functia Lagrange cu o constanta arbitrara, forma ecuatiilor de miscare nu se schimba (acest fapt este legat de arbitrariul alegerii unitatilor de masura).

Daca un sistem mecanic este alcatuit din doua parti suficient de indepartate pentru ca interactiunea lor sa dispara, functia Lagrange a sistemului devine egala cu suma functiilor Lagrange ale partilor izolate:

unde

cu f - functie oarecare de clasa C² , forma ecuatiilor de miscare nu se schimba. O astfel de transformare se numeste transformare de etalonare. Actiunea corespunzatoare functiei :

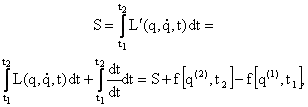
difera de actiunea S printr-un termen constant care dispare cand punem conditia de extrem:

astfel incat forma ecuatiilor de miscare ramane aceeasi.

Functia L depinde doar de si eventual de timp dar nu depinde de derivatele de ordin superior lui .

Principiul relativitatii in mecanica clasica (Galilei)

Studiul miscarii unui sistem mecanic necesita alegerea unui sistem de referinta (un corp rigid de referinta caruia i se ataseaza un sistem de axe de coordonate si un ceas, solidar cu acesta).

Clasa referentialelor este foarte larga. Exista printre acestea unele in care spatiul fizic este omogen (toate pozitiile fiind echivalente) si izotrop (toate directiile fiind echivalente) iar timpul curge uniform (toate momentele fiind echivalente). Aceste sisteme de referinta se numesc inartiale (S.R.I.). Faptul ca nu exista un punct privilegiat in spatiu sau o directie privilegiata, ca si inexistenta unui moment privilegiat constituie proprietati structurale intrinseci ale spatiului si timpului.

se reduc la : deoarece . In acest caz, Deoarece este functie doar de viteza, rezulta ca: adica legea inertiei.

Cunoscand functia Lagrange a unui sistem mecanic putem obtine atat ecuatiile de miscare cat si legile de conservare pentru acel sistem. In constructia acestei functii tinem cont de :

Principiul de invarianta: in mecanica clasica ecuatiile de miscare

Euler-Lagrange trebuie sa-si pastreze forma la o schimbare a

reperului inertial;

Principiul superpozitiei: lagrangeianul unui sistem se compune din

lagrangeianii partilor izolate, din termeni care corespund interactiilor

liniare si termeni ce corespund interactiei fiecarei parti cu campurile

externe;

Principiul de corespondenta: functia Lagrange trebuie sa fie astfel

construita incat rezultatele obtinute sa coincida cu cele ale mecanicii

newtoniene;

Proprietati de simetrie fizica: alegerea coordonatelor generalizate sa

Vom considera un caz simplu pentru inceput: functia L a unui punct material liber in miscare fata de un S.R.I.. Din proprietatile de omogenitate si izotropic spatiala si din proprietatea de uniformitate a timpului rezulta ca functia Lagrange ar putea depinde doar de modulul vitezei:

Vom postula ca functia Lagrange in acest caz este o functie omogena in sensul lui Euler de ordinul intai in v² .

Definitie: O functie este omogena de ordinul n in variabila x daca fiind un parametru. Daca derivam aceasta relatie in raport cu :

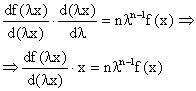
si punem , obtinem:

- teorema lui Euler pentru functia omogena. In cazul unor functii de mai multe variabile, aceasta teorema capata forma:

Derivam expresia de mai sus in raport cu v² :

si obtinem :

Viteza fiind arbitrara, rezulta ca derivata se anuleaza si deci:

Prin integrare avem: si convenim sa notam constanta unde m reprezinta masa inertiala a punctului material .

Masa este o marime de stare a unui sistem, pozitiv definita, aditiva, constanta in timpul miscarii (ultima observatie este valabila doar in mecanica clasica).

In concluzie, functia Lagrange a unui punct material izolat este:

Daca consideram un sistem de puncte materiale care nu interactioneaza, functia Lagrange fiind aditiva:

In coordonate carteziene:

In coordonate cilindrice:

In coordonate cilindrice:

Interactiunea punctelor materiale se considera introducand in functia Lagrange a unui sistem de puncte materiale care nu interactioneaza, un termen care exprima intercatiunea - o functie bine determinata de coordonate, a carei forma depinde de natura interactiunii: . Functia Lagrange capata forma:

sau L=T-U, unde este energia cinetica iar este energia potentiala a sistemului.

Forma functiei Lagrange pentru un sistem inchis de puncte materiale indica faptul ca transformarea lasa functia Lagrange neschimbata si implicit si ecuatiile de miscare neschimbate. Aceasta inseamna ca timpul este si izotrop si ca orice miscare mecanica este reversibila. De asemenea din faptul ca energia potentiala depinde doar de pozitiile punctelor materiale la un moment dat rezulta ca modificarea pozitiei unui punct material se rasfrange instantaneu asupra tuturor celorlalte. In mecanica clasica interactiunile se propaga cu o viteza infinita, instantaneu. Aceasta este o consecinta a principiului timpului absolut si a principiului relativitatii.

Ecuatiile Euler-Lagrange, in cazul functiei Lagrange exprimata in coordonate carteziene, capata forma:

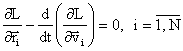
Tinand cont de forma functiei Lagrange, ele devin: si poarta numele de ecuatiile lui Newton. Cantitatea este forta care actioneaza asupra punctului material "i".

Functia Lagrange a unui sistem aflat in camp de forte exterioare se obtine prin urmatorul rationament . Daca se considera un sistem izolat format din doua parti A si B care interactioneaza intre ele, miscarea lui B fiind cunoscuta (se dau functiile functia Lagrange a acestui sistem va fi

Inlocuind si cu functii cunoscute de timp obtinem:

Termenul fiind o functie numai de timp poate fi exprimat ca derivata totala la timp a unei alte functii de timp si deci, in acord cu cea de-a treia proprietate a functiei Lagrange, poate fi exclus din expresia lagrangianului:

Aceasta functie Lagrange descrie sistemul A in campul de forte propus de sistemul B a carui miscare se cunoaste. Spre deosebire de functia Lagrange a unui sistem inchis acum energia potentiala poate contine explicit timpul.